दो कला संबद्ध, एकवर्णी (तरंग दैर्ध्य λ) स्रोतों, S1 और S1 पर विचार कीजिए, जो दूरी d द्वारा पृथक हैं। S1 और S2 की तीव्रताओं का अनुपात (जो बिंदु P पर व्यतिकरण के लिए उत्तरदायी है, जहाँ संसूचक स्थित है) 4 है। S1 से बिंदु P की दूरी है: (यदि बिंदु P पर परिणामी तीव्रता, S1 की तीव्रता के 94 गुना के बराबर है) (दिया गया है: ∠S2S1P=90∘,d>0 और n एक धनात्मक पूर्णांक है)
d2−n2λ22nλ
d2+n2λ22nλ
nλd√d2−n2λ2
2nλd√d2−n2λ2
The correct Answer is:A
S1 की 94 तीव्रता =S2 की तीव्रता का 9 गुना
उच्चिष्ठ की तीव्रता =(√I1+√I2)2=9I2
⇒S2P−S1P=nλ उच्चिष्ठ के लिए
√d2+x2−x=nλ x=d2−n2λ22nλ
Topper's Solved these Questions
- JEE-MAIN TEST - 38 Book:NTA MOCK TESTSChapter:JEE-MAIN TEST - 38 Exercise:भौतिक विज्ञान(विषयपरक आंकिक)
Explore 5 Videos
- JEE-MAIN TEST 23 Book:NTA MOCK TESTSChapter:JEE-MAIN TEST 23 Exercise:भौतिक विज्ञान(विषयपरक आंकिक)
Explore 5 Videos
- JEE-MAIN TEST - 51Book:NTA MOCK TESTSChapter:JEE-MAIN TEST - 51Exercise:भौतिक विज्ञान(विषयपरक आंकिक)
Explore 5 Videos
Similar Questions
m द्रव्यमान की एक गेंद, जो v वेग से गतिमान है, विरामावस्था में एक लोलक के गोलक से टकराती है। गोलक का द्रव्यमान भी m है। यदि संघट्ट पूर्णतः अप्रत्यास्थ है, जिस ऊंचाई तक गोलक ऊपर जाएगा, h=v2x⋅g द्वारा दी जाती है, तो x का मान है:
View Solutionकोई पहाड़ी 500 m ऊँची है। किसी तोप द्वारा, जो पैकटों को 125 m/s की चाल से प्रक्षेपित कर सकती है। इस पहाड़ी के पार कोई आपूर्ति की जानी है। तोप पहाड़ी के आधार से 800m की दूरी पर स्थित है और पहाड़ी से इसकी दूरी समायोजित करने के लिए इसे पृथ्वी पर 2 m/s चाल से चलाया जा सकता है। वह अल्पतम समय परिकलित कीजिए जिसमें कोई पैकेट पहाड़ी के पार भूतल तक पहुंच सकता है। (g=10m/s2 लीजिए)
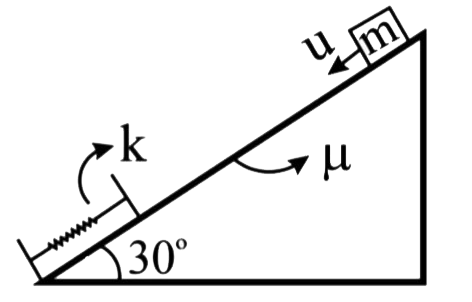
View Solution1 kg द्रव्यमान का एक गुटका μ=1√3 के एक खुरदरे आनत तल के शीर्ष से मुक्त किया जाता है। गुटके की प्रारंभिक चाल 2ms−1 है। चित्र के अनुसार नियतांक k=1Nm−1 की एक स्प्रिंग अज्ञात लंबाई के आनत तल के आधार से जुड़ी हुई है। स्प्रिंग का अधिकतम संपीडन ज्ञात कीजिए ।(उत्तर मीटर में दीजिए)।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionदो स्थिर बिंदु A और B के निर्देशांक क्रमशः (a,0) और (−a,0) है , तो चर बिंदु P का बिन्दुपथ ज्ञात कीजिए जबकि :
PA=nPB , जहाँ n अचर है ।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी बिंदु (1, 2) से दूरी उसकी y-अक्ष से दूरी की दो गुनी है ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु P का बिन्दुपथ ज्ञात कीजिए जो इस प्रकार गमन करता है कि बिंदु A(am,0),m≠1 से उसकी दूरी , बिंदु B(am,0) से उसकी दूरी की m गुनी रहती है ।
View SolutionA और B दो स्थिर बिंदु है जिनके निर्देशांक क्रमश : (a,0) और (−a,0) है । चर बिंदु P के बिन्दुपथ का समीकरण ज्ञात कीजिए , जबकि
PA+λPB=0 , जहाँ λ कोई अचर है ।
View Solutionमाना Sk=1+2+3+…+kk है। यदि S21+S22+….S210=512A है, तो A बराबर है
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionबिंदु P की बिंदु (4,3) से दूरी √10 है। बिंदु P के निर्देशांक ज्ञात कीजिए यदि इस की कोटि भुज से दुगुनी हो।
View Solution
