निम्नलिखित समीकरण - युग्मो (i) से (iv) मे p और (v) मे p तथा qके मान ज्ञात कीजिए।
−3x+5y=7 और 2px−3y=1 यदि इन समीकरणों द्वारा निरूपित रेखाएँ एक अद्वितीय बिंदु पर प्रतिच्छेद करती है
The correct Answer is:निरूपित रेखाएँ अद्वितीय बिंदु पर प्रतिच्छेद करेगी
Topper's Solved these Questions
- दो चरों वाले रैखिक समीकरण - युग्म BOOK - BHARATI BHAWANCHAPTER - दो चरों वाले रैखिक समीकरण - युग्म EXERCISE - प्रश्नमाला 3A
17 Videos
- दो चरों वाले रैखिक समीकरण - युग्म BOOK - BHARATI BHAWANCHAPTER - दो चरों वाले रैखिक समीकरण - युग्म EXERCISE - प्रश्नमाला 3B
28 Videos
- दो चरों वाले रैखिक समीकरण - युग्म BOOK - BHARATI BHAWANCHAPTER - दो चरों वाले रैखिक समीकरण - युग्म EXERCISE - प्रश्नमाला 3F (बहुवैकल्पिक प्रश्न)
27 Videos
- त्रिभुज BOOK - BHARATI BHAWANCHAPTER - त्रिभुज EXERCISE - प्रश्नमाला 7E (बहुवैकल्पिक प्रश्न) सही विकल्प का चयन करें।
17 Videos
- द्विघात समीकरणBOOK - BHARATI BHAWANCHAPTER - द्विघात समीकरणEXERCISE - प्रश्नमाला 4 G (बहुवैकल्पिक प्रश्न)
20 Videos
Similar Questions
निम्नलिखित प्रत्येक प्रश्न मे दिए गए रैखिक समीकरण - युग्म को ग्राफ़ीय विधि से हल कीजिए
3x + 2y = 4
2 x - 3y = 7
View Solutionनिम्नलिखित समीकरण - युग्म को हल कीजिए
x + y = 3,
4 x - 3y = 26
View Solutionयदि 2 x + 3y = 12 तथा 3 x - 2y = 5 है, तो
View Solutionदी गई आकृति में, यदि DE||BC है, तो x बराबर है
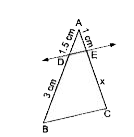
View Solutionनिम्नलिखित में कौन-सा द्विघात समीकरण है?
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए ,जो रेखाये x−y−6=0 तथा 7x−5y=36 के प्रतिच्छेद बिंदु को मूलबिंदु से मिलती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए , जो रेखाओ x+y=3 तथा 2x+3y=7 के प्रतिच्छेद बिंदु को रेखाओ 2x+3y=8 तथा 3x−y=1 के प्रतिच्छेद बिंदु से मिलती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखा 7x−5y+14=0 के समान्तर है तथा रेखाओ 2x+3y+7=0 और 3x−4y−15=0 के प्रतिच्छेद बिंदु से होकर जाती है ।
View Solutionसिद्ध कीजिए कि मूलबिंदु को एक उचित बिंदु(-1,-1) पर स्थान्तरित करके समीकरणों x+3y+4=0 और x−3y−2=0 को x+3y=0 तथा x−3y=0 के रूप में लिखा जा सकता है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionउस रेखा के समीकरण ज्ञात कीजिए जो बिंदु (−1,3,2) से होकर जाती है तथा रेखाओं x1=y2=z3 और x+2−3=y−12=z+15 पर लम्ब है।
View Solution
