एक रेखाखंड को दिए हुए अनुपात में विभाजित करना।

वीडियो समाधान

लिखित उत्तर

Verified by Experts

बच्चों इस रचना को समझने के लिए मान लेते है, एक रेखा $A B$ है जिसे हमे $m : n$ में विभाजित करना है, जहाँ $m = 3$ तथा $n = 2$ मान लेते है।

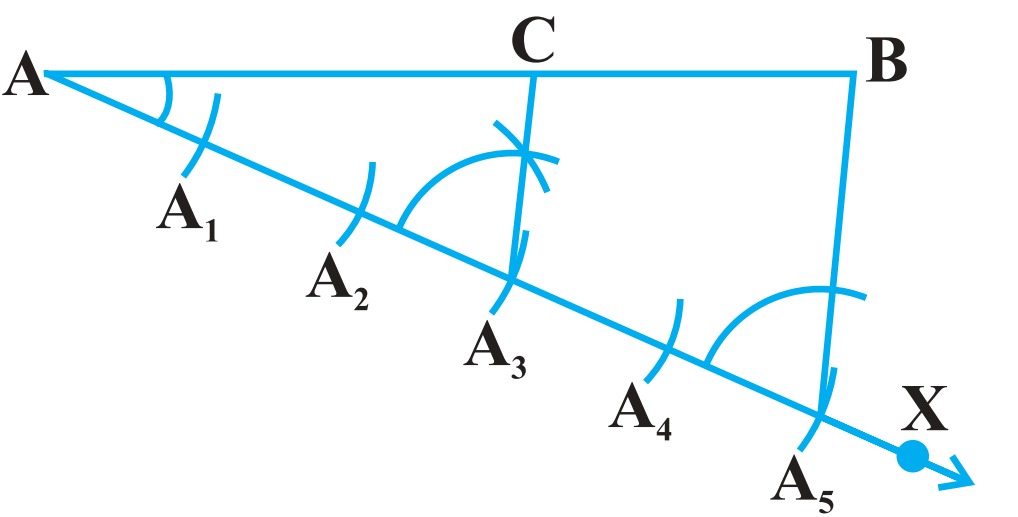
रचना के चरण:

चरण 1: बच्चों सबसे पहले $A B$ से नीचे की ओर एक न्यूनकोण बनाती हुई किरण $A X$ खींचिए।

चरण 2: अब $A X$ किरण पर $(m + n$ $= 3 + 2 = 5)$ 5 बिन्दु $A_{1}, A_{2}, A_{3}, A_{4}$ तथा $A_{5}$ इस प्रकार से चिन्हित करो की $A A_{1} = A_{1} A_{2}$ $= A_{2} A_{3}$ $= A_{3} A_{4}$ $= A_{4} A_{5}$ हो।

चरण 3: अब बिन्दु $B$ व बिन्दु $A_{5}$ मिलाकर $B A_{5}$ खींचिए।

चरण 4: अब $B A_{5}$ के समांतर एक रेखा बिन्दु $A_{3}$ (क्योंकि $m = 3$ इसलिए बिन्दु $A_{3}$ लिया है) से खींचिए जो रेखा $A B$ को बिन्दु $C$ पर मिलता है।

इसी के साथ हमारी रचना पूरी होती है, रेखा $A B$ , $A C$ व $C B$ में विभाजित हुई हैं, जहाँ $A C : C B = 3 : 2$

चित्र में देख सकते हैं कि $A A_{5} B$ एक त्रिभुज हैं, जिसमे इसकी एक भुजा $A_{5} B$ के समांतर एक रेखा $A_{3} C$ खींची गई है, तब :

आधारभूत समानुपातिकता प्रमेय द्वारा

$\frac{A A_{3}}{A_{3} A_{5}} = \frac{A C}{C B}$

और रचना से हम देख सकते है:

$\frac{A A_{3}}{A_{3} A_{5}} = \frac{3}{2}$

तब

$\frac{A C}{C B} = \frac{3}{2}$

अतः ये निष्कर्ष निकलता हैं, कि बिन्दु $C$ रेखा $A B$ को $3 : 2$ के अनुपात में विभाजित करता है।

वैकल्पिक विधि

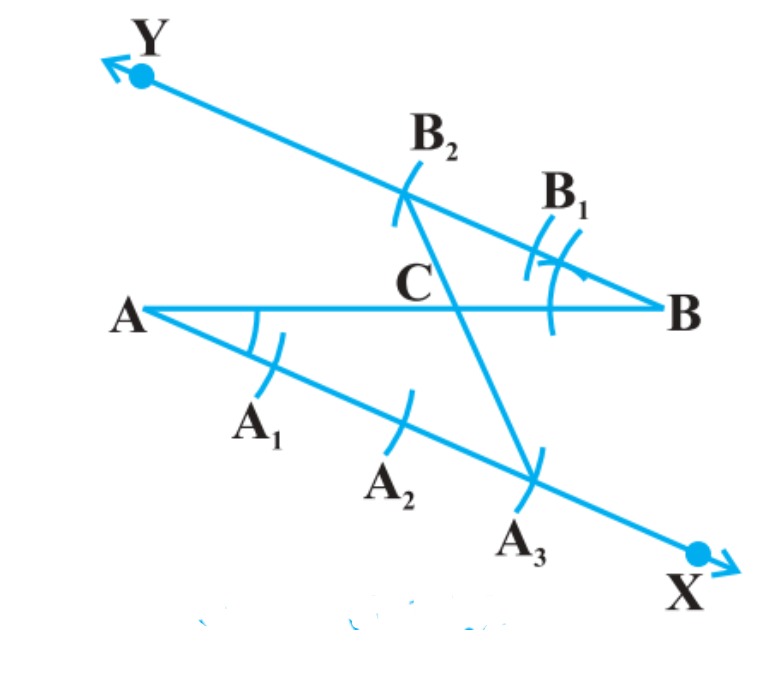
रचना के चरण:

चरण 1: $A B$ से न्यूनकोण बनाती कोई किरण $A X$ खींचिए।

चरण 2: $∠ B A$ X के बराबर $∠ A B Y$ बनाकर AX के समांतर एक किरण BY खींचिए।

चरण 3: AX पर बिंदु $A_{1}, A_{2}, A_{3}$ (m=3) और BY पर बिंदु $B_{1}, B_{2}$ (n = 2) इस प्रकार अंकित कीजिए कि

$A A_{1} = A_{1} A_{2} = A_{2} A_{3}$ $= B B_{1} = B_{1} B_{2}$ हो ।

चरण 4: $A_{3} B_{2}$ को मिलाइए। माना यह $A B$ को बिंदु $C$ पर प्रतिच्छेद करती है

तब $A C : C B$ $= 3 : 2$ है।

यहाँ $△ A A_{3} C$ ~ $△ B_{2} B C$

$\frac{A A_{3}}{B B_{2}}$ $= \frac{A C}{B C}$

परंतु रचना द्वारा $\frac{A A_{3}}{B B_{2}}$ $= \frac{3}{2}$

$\frac{A C}{B C}$ $= \frac{3}{2}$

वास्तव में इन विधियों द्वारा दिये गये रेखाखंड को किसी भी अनुपात में विभाजित किया जा सकता है।
अब हम ऊपर दी गई रचना को एक दिए गए त्रिभुज के समरूप एक अन्य त्रिभुज की रचना करने में उपयोग करेंगे जिसकी भुजाओं और दिए गए त्रिभुज की संगत भुजाओं में एक अनुपात दिया हुआ हो।

|

Updated on:21/07/2023

Class 10 MATHS CONSTRUCTIONS

समान प्रश्न

Recommended Questions

Home
Ask Doubt
Profile