सिद्ध कीजिए- sin4θ−cos4θ=1−2cos2θ.
Step by step video & image solution for सिद्ध कीजिए- sin^(4)theta-cos^(4)theta=1-2cos^(2)theta. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - प्रश्नमाला 13C (बहुवैकल्पिक प्रश्न )
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - प्रश्नमाला 13C (बहुवैकल्पिक प्रश्न )
20 Videos
- त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 10B (बहुवैकल्पिक प्रश्न)
13 Videos
- त्रिभुज BOOK - BHARATI BHAWANCHAPTER - त्रिभुज EXERCISE - प्रश्नमाला 7E (बहुवैकल्पिक प्रश्न) सही विकल्प का चयन करें।
17 Videos
Similar Questions
यदि sinA+sin2A=1 है, तो व्यंजक (cos2A+cos4A) का मान है
View Solutionयदि sinA+sin2A=1 है, तो व्यंजक (cos2A+cos4A) का मान है
View Solutionयदि tanθ=815 हो, तो cosecθ=?
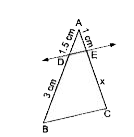
View Solutionदी गई आकृति में, यदि DE||BC है, तो x बराबर है
View SolutionIf sinθ+sin2θ=1,find the value of cos12θ+3cos10θ+3cos8θ+cos6θ+2cos4θ+2cos2θ−2
View SolutionThe value of sec2θ −sin2θ−2sin4θ2cos4θ−cos2θ
View Solutionsec^(2)theta-(sin^(2)theta-2sin^(4)theta)/(2cos^(4)theta-cos^(2)theta)=1
View SolutionProve that 2cos^(2)theta-cos^(4)theta+sin^(4)theta=1
View Solutionयदि cosθ=√32,तो सिद्ध करें कि 3sinθ−4sin3θ=1
View Solutionयदि sinθ+cosθ=x, तो सिद्ध कीजिए कि sin6θ+cos6θ=1−34(x2−1)2,x2≤2
View SolutionProve:
sin4θ−cos4θ=1−2cos2θ
View Solution" 1) sin4θ−cos4θ=1−2cos2θ
View SolutionIf tanθ=43,then the value of 3sinθ+2cosθ3sinθ−2cosθ is
View SolutionProve that sin4θ−cos4θ = 1−2cos2θ
View Solutionनिम्नलिखित सर्व समिकाओ को सिद्ध करो-
(i) (1−cosθ)(1+cosθ)(1+cot2θ)=1
(ii) (1+sinθ)2+(1−sinθ)2)2cos2θ=1+sinθ21−sin2θ
(iii) cos2θ(1−cosθ)sin2θ(1−sinθ)=1+sinθ1+cosθ
(iv) (sinθ−cosθ)2=1−2sinθ.cosθ
(v) (sinθ+cosθ)2+(sinθ−cosθ)2=2
(vi) (asinθ+bcosθ)2+(acosθ−bsinθ)2=a2+b2
(vii) cos4A+sin4A+2sin2A.cos2A=1
(ix) (cos4θ−sin4θ)=cos2θ−sin2θ=2cos2θ−1
(x) 2cos2θ−cos4θ+sin4θ=1
(xi) 1−2cos2θ+cos4θ=sin4θ
(xii) 1−2sin2θ+sin4θ=cos4θ
View Solutionसिद्ध करा sin4θ−cos4θ=1−2cos2θ
View Solution
