सिद्ध कीजिए कि किसी समकोण त्रिभुज के कर्ण का मध्यबिंदु उसके सभी शीर्षों से समदूरस्थ होता है।
The correct Answer is:OA=OB=OC
Topper's Solved these Questions
- वृत्त BOOK - BHARATI BHAWANCHAPTER - वृत्त EXERCISE - प्रश्नगाला 12A
11 Videos
- वृत्त BOOK - BHARATI BHAWANCHAPTER - वृत्त EXERCISE - प्रश्नगाला 12B
6 Videos
- रेखाएँ और कोण BOOK - BHARATI BHAWANCHAPTER - रेखाएँ और कोण EXERCISE - प्रश्नमाला 7D (बहुवैकल्पिक प्रश्न)
21 Videos
- संख्या पद्धति BOOK - BHARATI BHAWANCHAPTER - संख्या पद्धति EXERCISE - प्रश्नमाला 1H (बहुवैकल्पिक प्रश्न)
45 Videos
Similar Questions
10 cm निज्या वाले वृत्त की एक जीवा की लंबाई 16 cm है। वृत्त के केंद्र से उस जीवा की दूरी ज्ञात कीजिए।
View Solutionदी गई आकृति में, वृत्त का केंद्र O है। यदि ∠OAB=40∘ तथा ∠OCB=30∘ है, तो ∠AOC ज्ञात कीजिए।
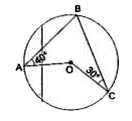
View Solutionदी गई आकृति में x का मान है

View Solutionनिम्नलिखित में से कौन सी संख्या परिमेय है ?
View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक सरल रेखा , अक्षो के साथ ऐसा समकोण त्रिभुज बनातीं है कि जिसके कर्ण कि लम्बाई √53 तथा क्षेत्रफल 7 वर्ग इकाई है । रेखा का समीकरण ज्ञात कीजिए
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज की भुजाओ से समदूरस्थ बिंदु कहलाता है-
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
View Solutionउस त्रिभुज का अतः केंद्र ज्ञात कीजिए जिसके शीर्षों के निर्देशांक (1,2),(2,3) और (3,1) है ।
View Solution
