माना कि f:R→R एक संतत विषम फलन है जिसका मान केवल एक बिन्दु पर ही शून्य होता है तथा f(1)=12 कि सभी x∈[−1,2] के लिए F(x)=∫x−1f(t)dt एवं सभी x∈[−1,2] के लिए G(x)=∫1−1t|f(f(t))|dt हैं | यदि limx→1F(x)G(x)=114 है, तब f(12) का मान है
Step by step video & image solution for माना कि f: R rarr RR एक संतत विषम फलन है जिसका मान केवल एक बिन्दु पर ही शून्य होता है तथा f(1)=1/2 कि सभी x in [-1, 2] के लिए F(x) = int_(-1)^(x) f(t)dt एवं सभी x in[-1, 2] के लिए G(x) = int_(-1)^(1) t|f(f(t))|dt हैं | यदि lim_(x rarr1) (F(x))/(G(x))=1/14 है, तब f(1/2) का मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 2)
8 Videos
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 3)
4 Videos
- JEE ADVANCED पेपर - 2 (2014)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )
4 Videos
- JEE ADVANCED पेपर - 2 (2016)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- III गणित (खंड-3)
4 Videos
Similar Questions
माना कि सभी x∈(−π2,π2) के लिए, f(x)=7tan8x+7tan6x−3tan4x−3tan2x है, तब सही कथन है (हैं)
View Solutionमाना कि बॉक्स I में n1 लाल गेंद और n2 काली गेंद हैं । माना कि बॉक्स II में n3 लाल गेंद और n4 काली गेंद हैं ।
बॉक्स I और बॉक्स II में से, यादृच्चया (at random) एक बॉक्स को चुना गया और इस चुने हुए बॉक्स से, यादृच्चया एक गेंद निकाली गयी । यह गेंद लाल रंग की पाई गयी । यदि इस लाल गेंद के बॉक्स II से निकाले जाने की प्रायिकता 13 है, तब निम्नलिखित में से n1,n2,n3 और n4 के सही संभव मान है (हैं)
View Solutionइस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
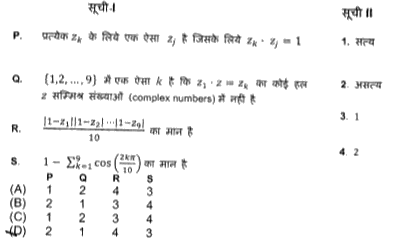
View Solutionअनुच्छेद
फुटबॉल दलों T1 और T2 को एक दूसरे के विरुद्ध दो खेल (games) खेलने हैं। यह मान लिया गया है कि दोनों खेलों के परिणाम
एक दूसरे पर निर्भर नहीं करते। दल T1 के दल T2 के विरुद्ध एक खेल में जीतने, बराबर होने और हारने की प्रायिकता क्रमशः 12,16
और 13 हैं। प्रत्येक दल जीतने पर 3 अंक, बराबरी पर 1 अंक और हारने पर 0 अंक अर्जित करता है। माना कि दो खेलों के पश्चात दल
T1 और दल T2 के द्वारा अर्जित कुल अंक क्रमशः X और Y हैं।
P(X>Y) का मान है
View SolutionLet F(x)=f(x)+f(1x),w h e r ef(x)=∫xtlogt1+tdt. (1) 12 (2) 0 (3) 1 (4) 2
View Solutionf(x)=∫π0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) is 12
View SolutionIf F(x)=int_(1)^(x)(ln t)/(1+t+t^(2))dt then F(x)=-F((1)/(x))
View SolutionIf int_(0)^(x)f(t)dt=x^(2)+int_(x)^(1)t^(2)f(t)dt, then f'((1)/(2)) is
View SolutionIf int_(0)^(x)f(t)dt=x+int_(x)^(1)f(t)dt ,then the value of f(1) is
View SolutionIf f(x)=∫x1logt1+tdtthenf(x)+f(1x) is equal to
View SolutionIf f(x)=∫x0{f(t)}−1dt, and ∫10{f(t}−1dt=√2, then f(x)=
View SolutionIf int_(0)^(x) f ( t) dt = x + int_(x)^(1) tf (t) dt , then the value of f(1) is
View Solutionएक द्विघात बहुपद f(x), जो f(0)=0,f(1)=1,f'(x)>0, को सभी x∈(0,1) के लिए संतुष्ट करता है, है
View Solutionमाना कि f:R→R एक सतत विषम फलन है जिसका मान केवल एक बिंदु पर ही शून्य होता है तथा f(1)=12 है। माना कि सभी xε[−1,2] के लिए F(x)=∫x1f(t)dt एवं सभी xε[−1,2] के लिए G(x)=∫x−1t|f(f(t))|dt है। यदि limx→1F(x)G(x)=114 है तब f(12) का मान है।
View Solutionयदि वास्तविक मान फलन f(x)=ax−1xn(ax+1) सम है, तब n का मान है
View Solutionयदि f(x)=Asin(πx2)+B,.f'(12)=√2 तथा ∫10f(x)dx=2Aπ तब A तथा B के मान है
View Solution
