माना कि दीर्घ वृत x29+y25=1 की नाभियाँ (foci) (f1,0) और (f2,0) हैं, जहाँ f1>0 और f2<0 हैं । माना कि P1 एवं P2 दो परवलय (parabola) हैं जिनकी नाभियाँ क्रमशः (f1,0) एवं (2f2,0) हैं तथा दोनों के शीर्ष (vertex) (0, 0) है । माना कि P1 की स्पर्श रेखा T1 बिन्दु (2f2,0) से, एवं P2 की स्पर्श रेखा T2 बिन्दु (f1,0) से गुजरती हैं । यदि T की प्रवणता (slope) m1 हो और T2 की प्रवणता m2 हो, तब (1m21+m22) का मान है
Step by step video & image solution for माना कि दीर्घ वृत x^2/9 +y^2/5 =1 की नाभियाँ (foci) (f_1,0) और (f_2, 0) हैं, जहाँ f_1 gt 0 और f_2 lt 0 हैं । माना कि P_1 एवं P_2 दो परवलय (parabola) हैं जिनकी नाभियाँ क्रमशः (f_1,0) एवं (2f_2, 0) हैं तथा दोनों के शीर्ष (vertex) (0, 0) है । माना कि P_1 की स्पर्श रेखा T_1 बिन्दु (2f_2, 0) से, एवं P_2 की स्पर्श रेखा T_2 बिन्दु (f_1, 0) से गुजरती हैं । यदि T की प्रवणता (slope) m_1 हो और T_2 की प्रवणता m_2 हो, तब (1/m_1^2 +m_2^2) का मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 2)
8 Videos
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 3)
4 Videos
- JEE ADVANCED पेपर - 2 (2014)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )
4 Videos
- JEE ADVANCED पेपर - 2 (2016)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- III गणित (खंड-3)
4 Videos
Similar Questions
माना कि सभी x∈(−π2,π2) के लिए, f(x)=7tan8x+7tan6x−3tan4x−3tan2x है, तब सही कथन है (हैं)
View Solutionमाना कि बॉक्स I में n1 लाल गेंद और n2 काली गेंद हैं । माना कि बॉक्स II में n3 लाल गेंद और n4 काली गेंद हैं ।
बॉक्स I और बॉक्स II में से, यादृच्चया (at random) एक बॉक्स को चुना गया और इस चुने हुए बॉक्स से, यादृच्चया एक गेंद निकाली गयी । यह गेंद लाल रंग की पाई गयी । यदि इस लाल गेंद के बॉक्स II से निकाले जाने की प्रायिकता 13 है, तब निम्नलिखित में से n1,n2,n3 और n4 के सही संभव मान है (हैं)
View Solutionइस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
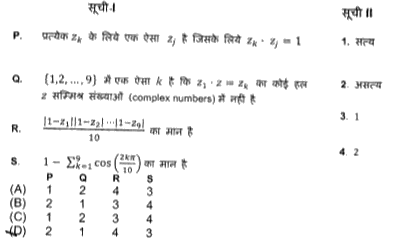
View Solutionअनुच्छेद
फुटबॉल दलों T1 और T2 को एक दूसरे के विरुद्ध दो खेल (games) खेलने हैं। यह मान लिया गया है कि दोनों खेलों के परिणाम
एक दूसरे पर निर्भर नहीं करते। दल T1 के दल T2 के विरुद्ध एक खेल में जीतने, बराबर होने और हारने की प्रायिकता क्रमशः 12,16
और 13 हैं। प्रत्येक दल जीतने पर 3 अंक, बराबरी पर 1 अंक और हारने पर 0 अंक अर्जित करता है। माना कि दो खेलों के पश्चात दल
T1 और दल T2 के द्वारा अर्जित कुल अंक क्रमशः X और Y हैं।
P(X>Y) का मान है
View SolutionSuppose that the foci of the ellipse x29+y25=1 are (f1,0)and(f2,0) where f1>0andf2<0. Let P1andP2 be two parabolas with a common vertex at (0, 0) and with foci at (f1.0)and (2f_2 , 0), respectively. LetT1 be a tangent to P1 which passes through (2f2,0) and T2 be a tangents to P2 which passes through (f1,0) . If m1 is the slope of T1 and m2 is the slope of T2, then the value of (1m12+m22) is
View Solutionमाना कि X={1,2,3,4,5,6,7,8,9}, माना कि X में सम्बन्ध R1 तथा R2 इस प्रकार हैं कि R1={(x,y):x−y,3 से विभाज्य हैं,x≠y} तथा R2={(x,y):{x,y}⊂{1,4,7} या {x,y}⊂{2,5,8} या {x,y}⊂{3,6,9} जहाँ ⊂ का अर्थ उपसमुच्चय से हैं| दिखाएं कि R1=R2
View Solutionदिया है कि ¯a⋅¯b=0 और ¯aׯb=¯0. सदिश ¯a और ¯b के बारे में आप क्या निष्कर्ष निकाल सकते हैं ?
View Solutionमाना कि ¯a और ¯b दो एकांक सदिश हैं | यदि सदिश ¯c=¯a+2¯b तथा ¯d=5¯a−4¯b परस्पर लम्ब हों, तो ¯a और ¯b के मध्य कोण है :
View Solution''स्तम्भ'अ'''''स्तम्भ'ब'''बिन्दु(−4,5)एवं(4,−5)के मध्य-बिन्दु के निर्देशांकy(0,3)एवं(4,0)के बीच की दुरी (x)मूल बिन्दु से(x,y)के बीच की दुरी0,0(0,y) बिन्दु की कोटि 5(x,0) बिन्दु की भुज√x2+y2
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
View Solutionपरवलय y2=2x की स्पर्श रेखा 18x-6y+1= 0 का स्पर्श बिन्दु है
View Solutionपरवलय y2=36x पर स्थित वे बिन्दु जिनकी कोटि भुज की तिगुनी है, हैं
View Solutionपरवलय y2=8x पर वह बिन्दु जिस पर खींचा गया अभिलम्ब रेखा x-2y+ 5 = 0 के समान्तर है, हैं
View Solution
