माना कि E1 और E2 दो दीर्घवृत हैं जिनके केन्द्र मूलबिन्दु हैं। E1 और E2 की दीर्घ अक्षायें क्रमशः x -अक्ष और y -अक्ष पर स्थित हैं । माना कि S:x2+(y−1)2=2 एक वृत्त है । सरल रेखा x + y = 3, वक्रों S, E1 और E2 को क्रमशः P, Q और R पर स्पर्श करती है । माना कि PQ = PR =2√23 है । यदि e1और e2 क्रमशः E1 और E2 की उत्केंद्रता (eccentricities) हैं, तब सही कथन है (हैं)
e21+e22=4340
e1e2=√72√10
∣∣e21−e22∣∣=58
e1e2=√34
Step by step video & image solution for माना कि E_1 और E_2 दो दीर्घवृत हैं जिनके केन्द्र मूलबिन्दु हैं। E_1 और E_2 की दीर्घ अक्षायें क्रमशः x -अक्ष और y -अक्ष पर स्थित हैं । माना कि S : x^2 + (y-1)^2 = 2 एक वृत्त है । सरल रेखा x + y = 3, वक्रों S, E_1 और E_2 को क्रमशः P, Q और R पर स्पर्श करती है । माना कि PQ = PR = (2sqrt2)/3 है । यदि e_1और e_2 क्रमशः E_1 और E_2 की उत्केंद्रता (eccentricities) हैं, तब सही कथन है (हैं) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 3)
4 Videos
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 3)
4 Videos
- JEE ADVANCED पेपर - 2 (2014)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )
4 Videos
- JEE ADVANCED पेपर - 2 (2016)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- III गणित (खंड-3)
4 Videos
Similar Questions
माना कि बॉक्स I में n1 लाल गेंद और n2 काली गेंद हैं । माना कि बॉक्स II में n3 लाल गेंद और n4 काली गेंद हैं ।
बॉक्स I और बॉक्स II में से, यादृच्चया (at random) एक बॉक्स को चुना गया और इस चुने हुए बॉक्स से, यादृच्चया एक गेंद निकाली गयी । यह गेंद लाल रंग की पाई गयी । यदि इस लाल गेंद के बॉक्स II से निकाले जाने की प्रायिकता 13 है, तब निम्नलिखित में से n1,n2,n3 और n4 के सही संभव मान है (हैं)
View Solutionमाना कि बॉक्स I में n1 लाल गेंद और n2 काली गेंद हैं । माना कि बॉक्स II में n3 लाल गेंद और n4 काली गेंद हैं ।
बॉक्स I और बॉक्स II में से, यादृच्चया (at random) एक बॉक्स को चुना गया और इस चुने हुए बॉक्स से, यादृच्चया एक गेंद निकाली गयी । यह गेंद लाल रंग की पाई गयी । यदि इस लाल गेंद के बॉक्स II से निकाले जाने की प्रायिकता 13 है, तब निम्नलिखित में से n1,n2,n3 और n4 के सही संभव मान है (हैं)
View Solutionइस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
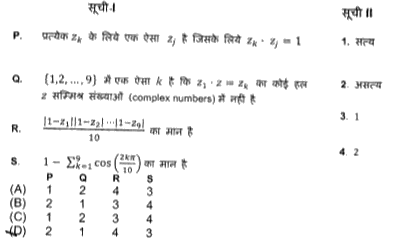
View Solutionअनुच्छेद
फुटबॉल दलों T1 और T2 को एक दूसरे के विरुद्ध दो खेल (games) खेलने हैं। यह मान लिया गया है कि दोनों खेलों के परिणाम
एक दूसरे पर निर्भर नहीं करते। दल T1 के दल T2 के विरुद्ध एक खेल में जीतने, बराबर होने और हारने की प्रायिकता क्रमशः 12,16
और 13 हैं। प्रत्येक दल जीतने पर 3 अंक, बराबरी पर 1 अंक और हारने पर 0 अंक अर्जित करता है। माना कि दो खेलों के पश्चात दल
T1 और दल T2 के द्वारा अर्जित कुल अंक क्रमशः X और Y हैं।
P(X>Y) का मान है
View Solutionमाना कि X={1,2,3,4,5,6,7,8,9}, माना कि X में सम्बन्ध R1 तथा R2 इस प्रकार हैं कि R1={(x,y):x−y,3 से विभाज्य हैं,x≠y} तथा R2={(x,y):{x,y}⊂{1,4,7} या {x,y}⊂{2,5,8} या {x,y}⊂{3,6,9} जहाँ ⊂ का अर्थ उपसमुच्चय से हैं| दिखाएं कि R1=R2
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View SolutionE1,E2 are events of a sample sapce such that P(E1) =1/4 , P(E2∣E1)=1/2,P(E1∣E2)=1/4. Then P(E1∣E2)+P(E1∣¯¯¯¯E2)=
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionकिसी अभिप्रयोग की दो घटना E1औरE2 है और इसके प्रायिकता P(E1) तथाP(E2) हैं तो निम्न में सत्य कौन-सा है?
View SolutionTwo circles with centres P and Q of radii 7 cm and 3cm, respectively, touch each other externally at a point A. BC is a direct common tangent to these two circles where B and C are the point on the circles respectively. The length of BC is: केंद्र P और Q के साथ दो दो वृत्त, जिनकी त्रिज्याएँ क्रमशः 7 सेमी और 3 सेमी है , एक दूसरे को बाहरी रूप से स्पर्श करते हैं। BC इन दो वृत्त में एक सीधा स्पर्शरेखा है जहां क्रमशः छ और C वृत्त पर बिंदु हैं। BC की लंबाई है
View SolutionIf e_1 and e_2 are the eccentricities of the hyperbola x^2/a^2-y^2/b^2=1 and y^2/b^2-x^2/a^2=1 then show that 1/e_1^2+1/e_2^2=1 .
View SolutionIf E1 and E2 are independent events associated with an experiment such that P(E1)=P1 and P(E2)=P2. Find
P(E1andE2).
View Solution
