दो 'मुक्त' (free) बिंदु-आवेश + 4 e तथा +e परस्पर a दूरी पर है। इनके बीच तीसरा बिंदु-आवेश q कहाँ रखा जाए। कि सम्पूर्ण निकाय संतुलन में रहे ? इस दशा में q का मान तथा चिन्ह क्या होंगे? संतुलन कैसा होगा?
माना कि आवेशों +4e तथा e के बीच स्थित संतुलित आवेश q की +4e से दूरी x है। स्पष्ट है कि इसकी आवेश +e से दूरी (a−x) होगा। आवेश q के अतिरिक्त मुक्त आवेशों +4e तथा +e को भी संतुलित रखना है।
आवेश 4e पर आवेश +e के कारण एक प्रतिकर्षण-बल F लगेगा । अत: इसके संतुलन के लिये इस पर आवेश के कारण लगने वाला बल F', बल F के 'विपरीत' व बराबर होना चाहिए। यह तभी सम्भव है जब आवेश q ऋणात्मक हो। ऐसा ही आवेश +e के संतुलन के लिये आवश्यक है।

आवेश +4e पर, आवेश +e के कारण वैद्युत (प्रतिकर्षण) बल
F=14πε04e×ea2
इस प्रकार, आवेश +4e पर, आवेश −q के कारण वैद्युत (आकर्षण) बल
F'=14πε04e×qx2
आवेश +4e के संतुलन के लिए, F=F'
∴4e2a2=4eqx2.....(i)
आवेश −q के संतुलन के लिये इस पर आवेश +4e के कारण लगने वाला (आकर्षण) बल F1, आवेश +e के कारण लगने वाले (आकर्षण) बल F2 के बराबर होना चाहिए, अर्थात
F1=F2
अथवा 14πε04e×qx2=14πε0e×q(a×x)2
अथवा 4eqx2=eq(a−x)2
∴x=a3
x का यह मान समीकरण (i) में रखकर हल करने पर
q=4e/9
अत: पूरे निकाय के संतुलन के लिये एक 4e/9 परिमाण का ऋण आवेश, +4e आवेश से 2a/3 दूरी पर रखना होगा। इस दशा में प्रत्येक आवेश पर नैट बल शून्य होगा। इस दशा में प्रत्येक आवेश पर नैट बल शून्य होगा। संतुलन अस्थायी होगा।
Topper's Solved these Questions
- कॉलम का नियम तथा वैद्युत क्षेत्र BOOK - NOOTAN HINDICHAPTER - कॉलम का नियम तथा वैद्युत क्षेत्र EXERCISE - वस्तुनिष्ठ प्रश्न
27 Videos
- कॉलम का नियम तथा वैद्युत क्षेत्र BOOK - NOOTAN HINDICHAPTER - कॉलम का नियम तथा वैद्युत क्षेत्र EXERCISE - अतिलघु उत्तरीय
36 Videos
- किरचॉफ के नियम तथा वैधुत परिपथ BOOK - NOOTAN HINDICHAPTER - किरचॉफ के नियम तथा वैधुत परिपथ EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए ( वस्तुनिष्ठ प्रकार प्रश्न )
42 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
39 Videos
Similar Questions
8 कूलॉम ऋण आवेश में विद्यमान इलेक्ट्रॉनों की संख्या है:
View Solutionएक धातु के गोले को वैद्युत से आवेशित किया जाता है। इस कथन का क्या तात्पर्य है?
View Solutionदिये गये परिपथ में प्रत्येक प्रतिरोध में धारा का मान है :
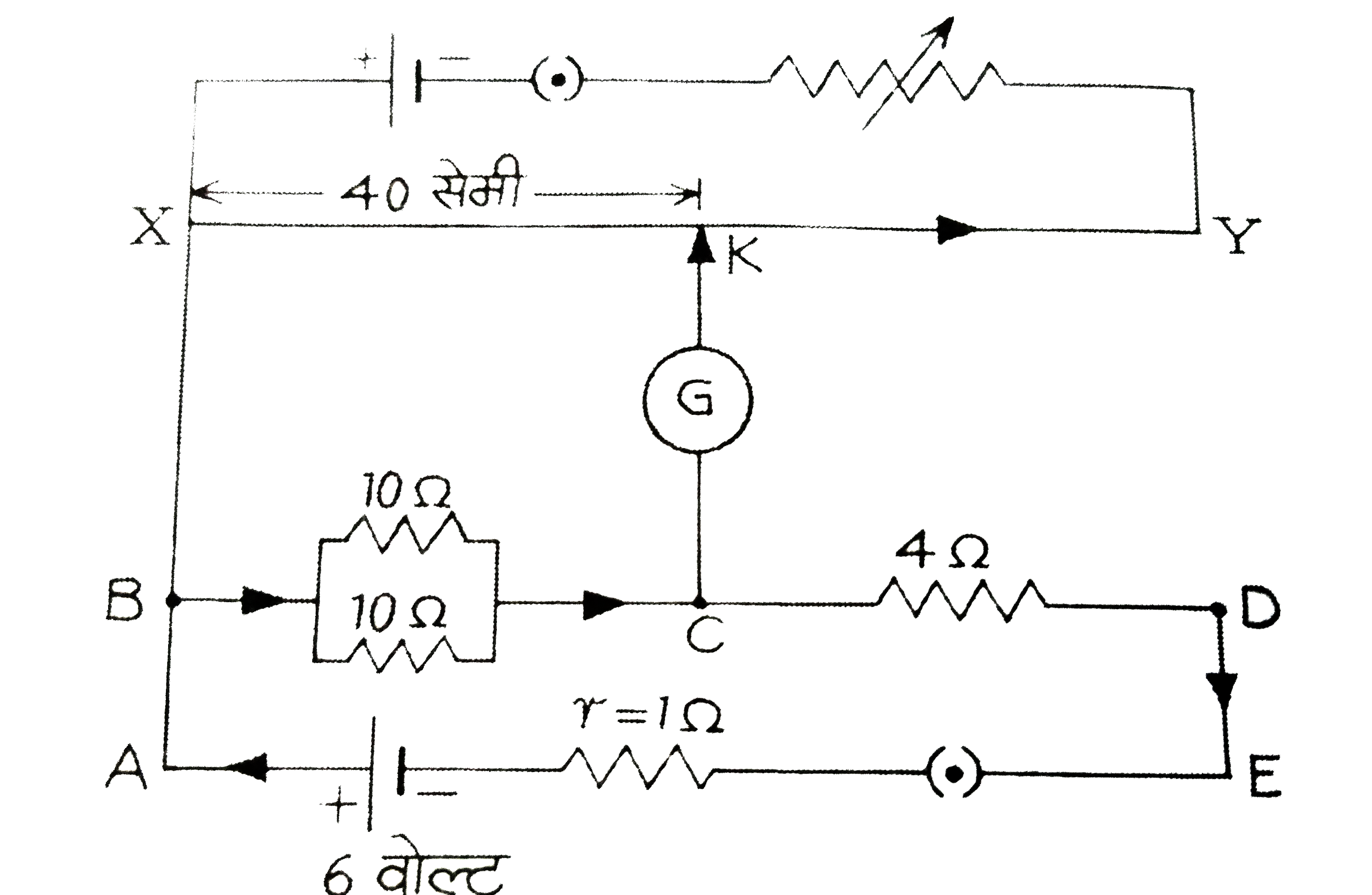
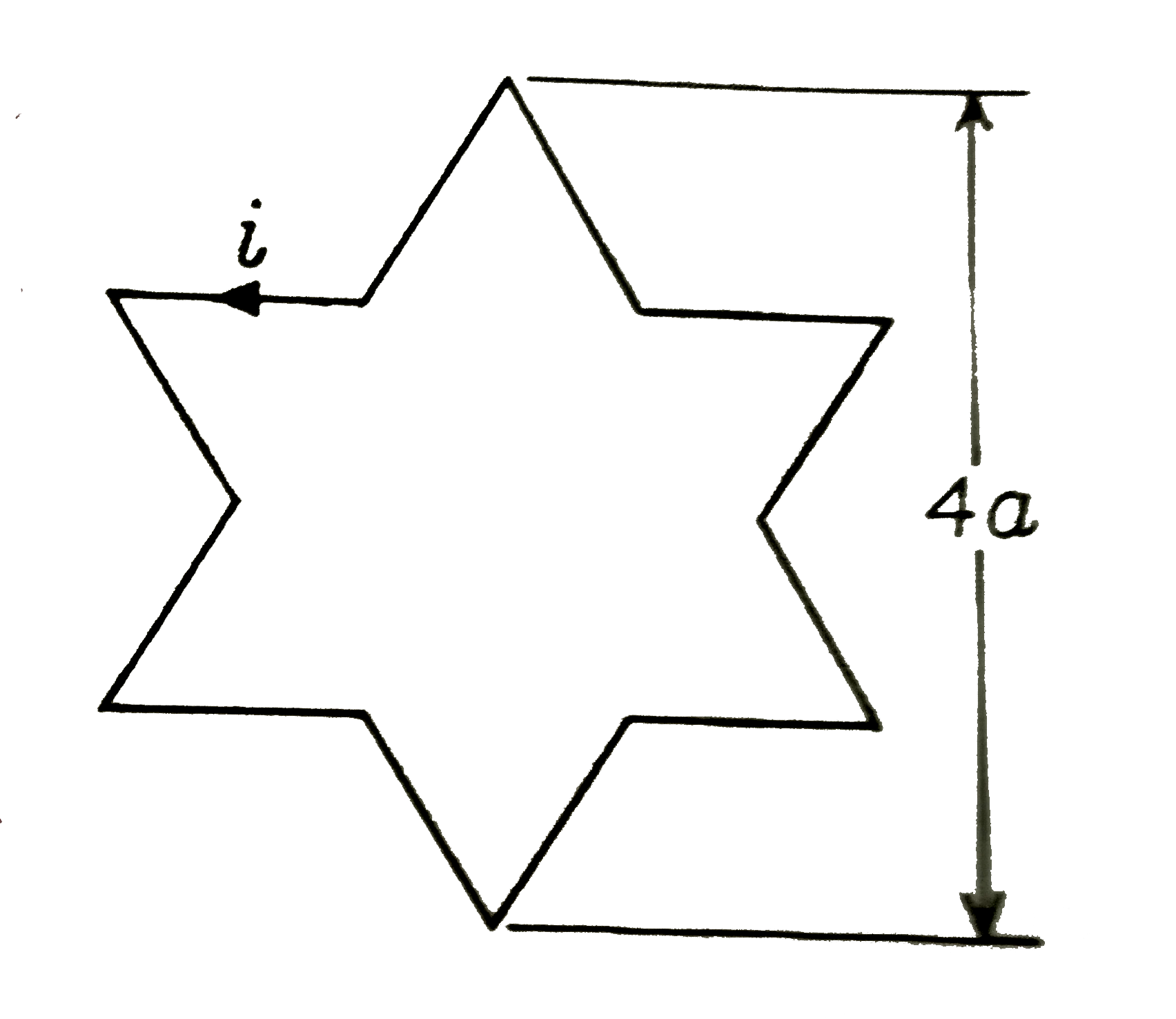
View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
View Solutionकिसी निकाय में दो आवेश qA=2.5×10−7C तथा qB=−2.5×10−7C क्रमश: दो बिंदुओं A:(0,0,−15cm) तथा B:(0,0,+15) पर स्थित है। निकाय का कुल आवेश तथा विद्युत द्विध्रुव आघूर्ण क्या है?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
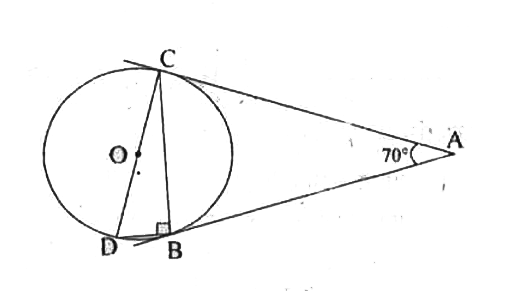
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
View Solutionउस बिंदु का बिन्दुपथ जो इस प्रकार गमन करता है कि बिंदु की दोनों अक्षों से दूरी सदैव समान रहती है ………… होगा ।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionदो विधुतरूधर ताँबे के समरूप आवेशित गोलों A और B में क्रमश: qA और qB आवेश है। उसी साइज का तीसरा अनावेशित गोला C पहले गोले A के संपर्क में रखा जाता है। तथा उसके बाद गोले B के संपर्क में रखा जाता है। अंत में दोनों से दूर कर दिया जाता है। A और B में नए आवेश क्या होंगे ?
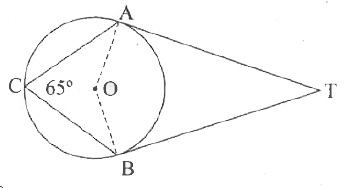
View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
View Solutionसंलगन आकृति में AT और BT दो स्पर्श रेखाएं है तथा वृत्त का केंद्र O है। यदि ∠AOT=55∘ हो ,तो ∠APB का मान क्या होगा ?
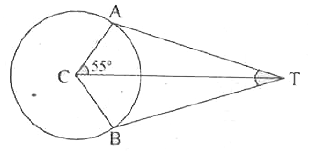
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -

View Solution
