बायो-सेवर्ट के नियम की सहायता से अनंत लम्बाई के धारावाही चालक के कारण r दुरी पर उत्पन्न चुंबकीय क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
Step by step video & image solution for बायो-सेवर्ट के नियम की सहायता से अनंत लम्बाई के धारावाही चालक के कारण r दुरी पर उत्पन्न चुंबकीय क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- गतिमान आवेश तथा चुंबकीय क्षेत्र Book:NOOTAN HINDIChapter:गतिमान आवेश तथा चुंबकीय क्षेत्र Exercise:आंकिक
Explore 54 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र Book:NOOTAN HINDIChapter:गतिमान आवेश तथा चुंबकीय क्षेत्र Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 39 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र Book:NOOTAN HINDIChapter:गतिमान आवेश तथा चुंबकीय क्षेत्र Exercise:लघु उत्तरीय
Explore 9 Videos
- कॉलम का नियम तथा वैद्युत क्षेत्र Book:NOOTAN HINDIChapter:कॉलम का नियम तथा वैद्युत क्षेत्र Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 16 Videos
- चल कुण्डली धारामापी Book:NOOTAN HINDIChapter:चल कुण्डली धारामापी Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 15 Videos
Similar Questions
एक समतल वृताकार कुंडली में 100 फेरे है। तथा उसकी त्रिज्या 3.0 सेमी है। इस कुण्डली में 2.0 ऐम्पियर की धारा प्रवाहित की जाती है । कुण्डली के अक्ष पर स्थित कुण्डली के केंद्र से 4.0 सेमी दुरी पर स्थित बिंदु पर चुंबकीय क्षेत्र की गणना कीजिए।
View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
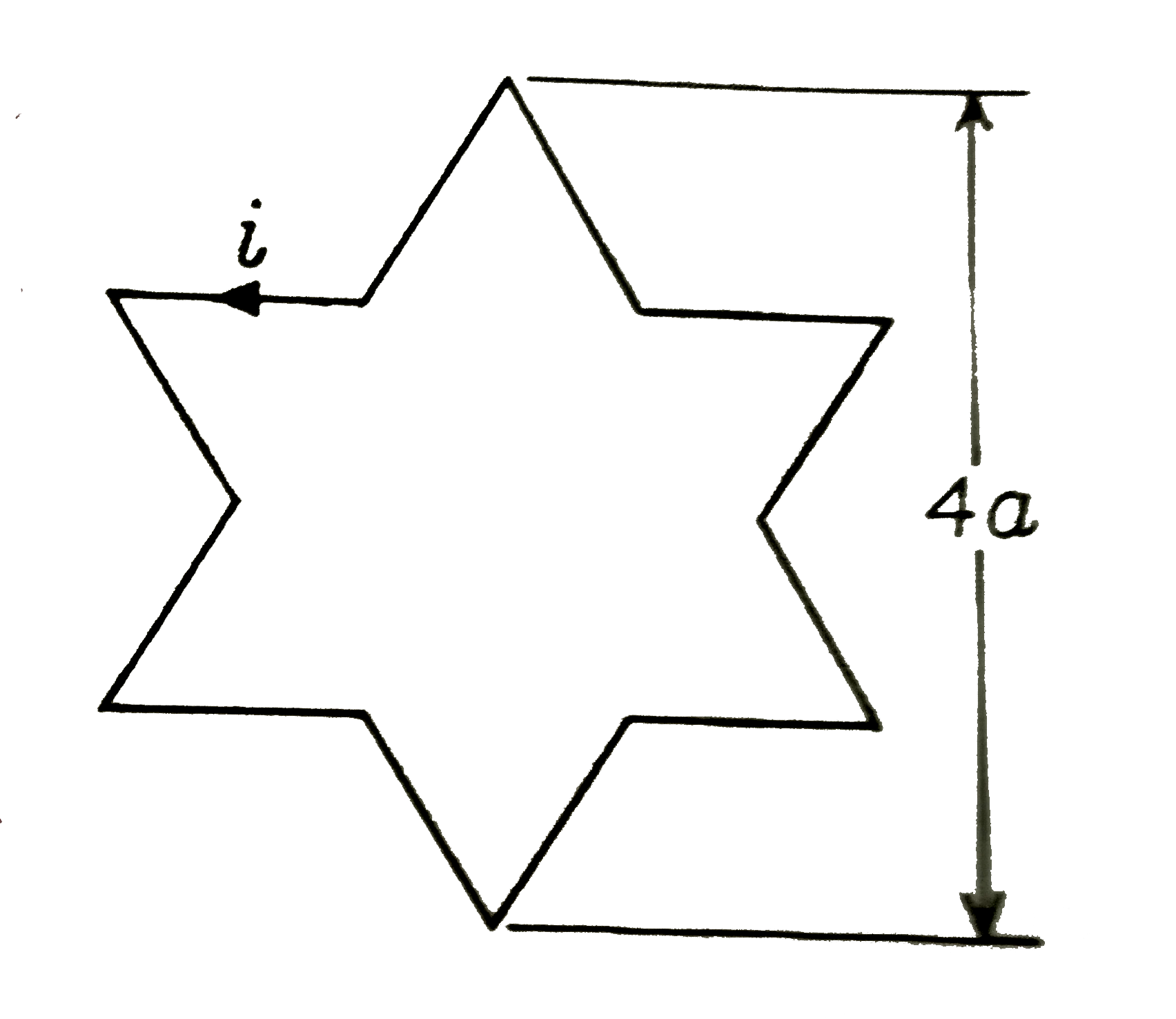
View Solutionधारावाही चालक के कारण उप्तन्न चुम्कीय क्षेत्र की तीव्रता से सम्बन्धित बाय-सेवर्ट नियम की व्यख्या कीजिए । बाय-सेवर्ट नियम के समीकरण की सहायता से निर्वात की चुंबकशीलता का मात्रक एवं विमीय समीकरण निकालिए।
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अंतर होता है। इनमे से एक −e है और दूसरा(e×Δe) है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो Δe कि कोटि होगी: (दिया है हाइड्रोजन का द्रव्यमान mh=1.67×10−27kg)
View Solutionआरेख में दण्ड (छड़) चुम्बको की व्यवस्थाओं के विन्यास दर्शाये गये है। प्रत्येक चुम्बक की द्विध्रुव आघूर्ण →M है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा?

View Solutionकिसी विद्युत धारावाही चालक के कारण चुंबकीय क्षेत्र
View Solutionविद्युत् धारावाही पाश के कारण चुंबकीय क्षेत्र
View SolutionJEE Special |धारावाही चालक के कारण चुंबकीय क्षेत्र | Part 1
View SolutionJEE Special |धारावाही चालक के कारण चुंबकीय क्षेत्र | Part 2
View Solutionधारावाही वलय , पट्टिका के कारण चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionसीधे धारावाही चालक तार के कारण किसी बिन्दु पर चुंबकिय क्षेत्र की तीव्रता
View Solutionअनन्त लम्बाई के ठोस बेलनाकार चालक का चुंबकीय क्षेत्र
View Solutionरेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता पर आधारित प्रश्न
View Solutionधारावाही चालक तार के कारण चुम्बकीय क्षेत्र
View Solution
