एक धारा-लूप का चुम्बकीय आघूर्ण है। लूप की अक्ष पर लूप के केन्द्र से दूरी पर चुम्बकीय क्षेत्र ज्ञात कीजिए।
|
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न15videos
चल कुण्डली धारामापी
- BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - दीर्घ उत्तरीय8videos
चल कुण्डली धारामापी
- BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न39videos
गतिमान आवेश तथा चुंबकीय क्षेत्र
- BOOK - NOOTAN HINDICHAPTER - तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतEXERCISE - वस्तुनिष्ट प्रकार प्रश्न ( एकल उत्तर प्रकार )1videos
तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांत
Similar Questions
आरेख में दण्ड (छड़) चुम्बको की व्यवस्थाओं के विन्यास दर्शाये गये है। प्रत्येक चुम्बक की द्विध्रुव आघूर्ण →M है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा?
 41:18View Solution
41:18View Solutionएकसमान चुम्बकीय क्षेत्र →B में N फेरों, A क्षेत्रफल तथा धारा i वाली कुण्डली पर लगने वाले बल के आघूर्ण का व्यंजक व्युत्पन्न कीजिए जबकि कुण्डली की अक्ष एवं चुम्बकीय क्षेत्र →B के बीच कोण θ है।
53:48View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
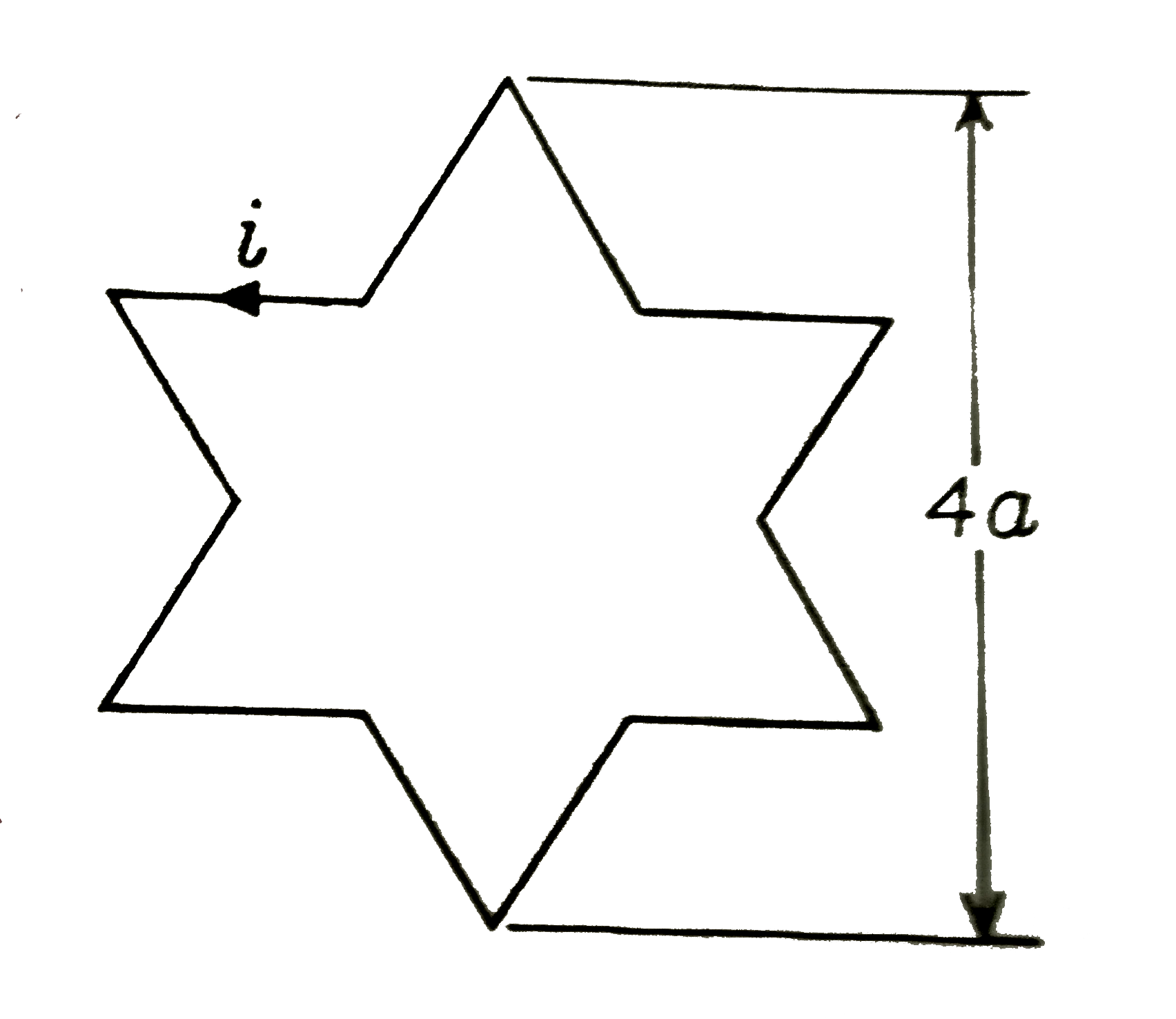 53:43View Solution
53:43View Solutionग्रीष्म ऋतु की गर्म रात्रि में , भू-तल के निकट , वायु का अपवर्तनांक न्यूनतम होता है । और भू-तल से ऊंचाई के साथ बढ़ता जाता है । यदि , कोई प्रकाश - किरणपुँज क्षैतिज दिशा में जा रहा हो तो हाइगेन्स के सिद्धान्त से यह परिणाम प्राप्त होता है कि, चलते हुए प्रकाश किरणपुँज :
01:18:11View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
04:27View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
49:03View Solutionचुम्बकीय द्विध्रुव तथा द्विध्रुव आघूर्ण | परिक्रमण करते इलेक्ट्रान का चुम्बकीय द्विध्रुव आघूर्ण | चुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता
45:31View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
55:10View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। उपरोक्त प्रश्न में अक्ष से दूरी पर चुम्बकीय क्षेत्र जहाँ a lt x lt b है
44:00View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
49:27View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
04:55View SolutionRecap|धारावाही लूप के कारण चुम्ब्कीय क्षेत्र
43:51View SolutionRecap|एकसमान चुम्ब्कीय क्षेत्र में धारावाही लूप पर बल आघूर्ण|Summary
53:51View SolutionRecap|धारा लूप चुम्बकीय द्विध्रुव के रूप में |परिभ्रमण करते इलेक्ट्रॉन का चुम्बकीय द्विध्रुव आघूर्ण |OMR|Summary
48:15View Solutionलूप क्या होता है ?
50:04View Solutionपरिनालिका के कारण चुम्बकीय क्षेत्र #!#आवेशित कण पर चुम्बकीय बल
28:40View Solution

