आलेख द्वारा निम्नलिखित रैखिक प्रोग्रामन समस्या को हल कीजिए :
निम्न व्यवरोधों के अन्तर्गत
x+y≤40
2x+y≤70
x≥0,y≥0
Z=5x+2y का अधिकतम मान ज्ञात कीजिए |
दी गई असमिकाओ को समीकरण में परिवर्तित करने पर ,
x+y=40 …(1)
2x+y=70 …(2)
x=0
y=0
समीकरण (1 ) तथा समीकरण (2 ) की सहायता से एक आरेख खींचते है और एक सुसंगत क्षेत्र प्राप्त करते है |
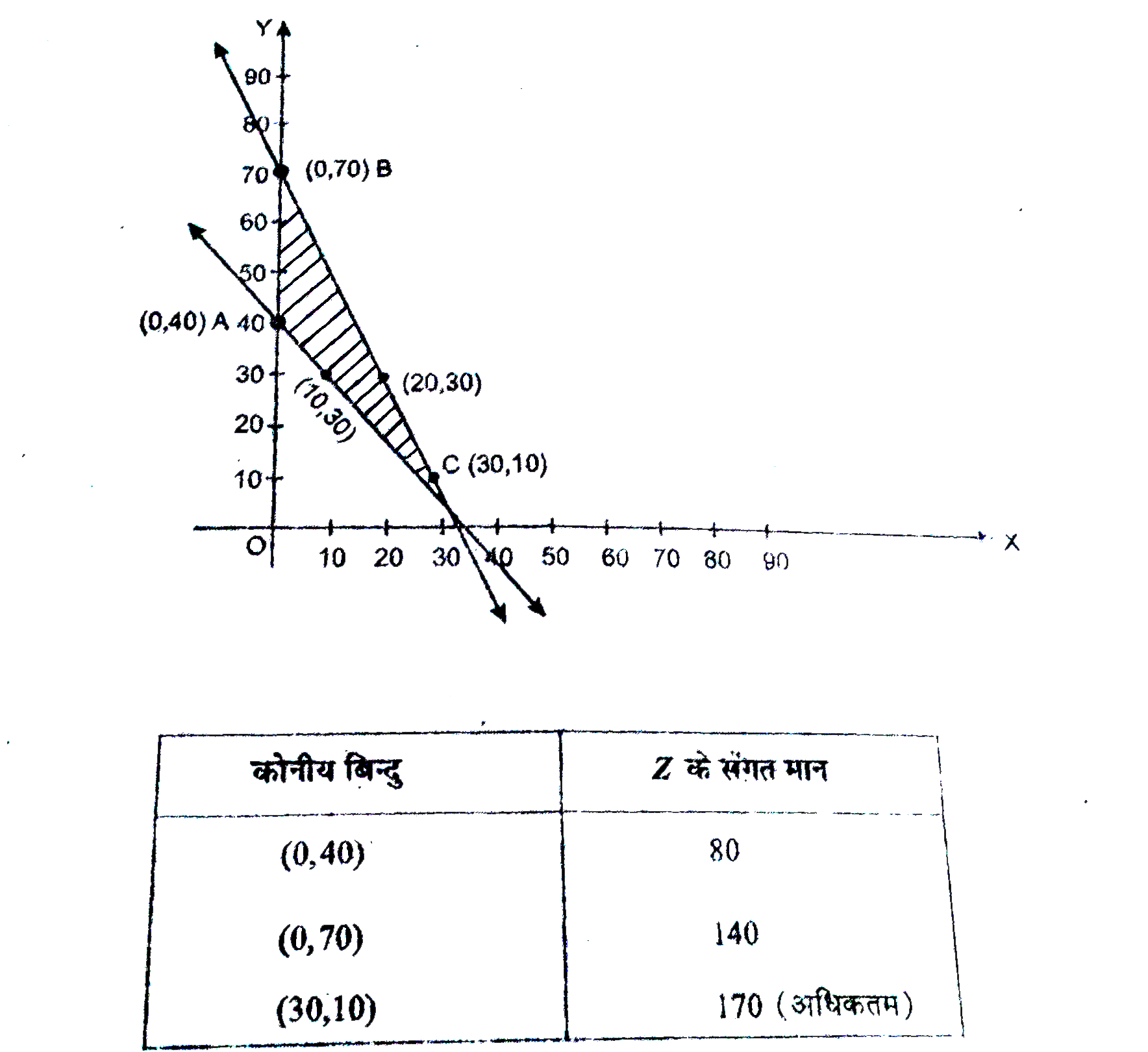
कोनीय बिन्दुओं A , B तथा C के निर्देशांक क्रमशः (0,40) , (0,70) तथा (30,10) है | अब प्रत्येक कोनीय बिन्दु पर का मान ज्ञात करते है |
अतः (30,10) बिन्दु पर का अधिकतम मान 170 है |
Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - रैखिक प्रोग्रामन EXERCISE - उदाहरण1videos
रैखिक प्रोग्रामन
- BOOK - MANOHAR RAYCHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्नावली 12(A)16videos
रैखिक प्रोग्रामन
- BOOK - MANOHAR RAYCHAPTER - प्रायिकता EXERCISE - इंजीनियरिंग परीक्षाओं के प्रश्न4videos
प्रायिकता
- BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न7videos
सततता तथा अवकलनीयता
Similar Questions
एक फल उत्पादक अपने बाग़ में दो प्रकार के खादों तथा ब्राण्डों का उपयोग कर सकता है मिश्रण के प्र्तेक थैले में नाइट्रोजन ,फास्फोरिक अम्ल , पोटॉश और क्लोरीन की मात्रा (किग्र में ) सारणी में दी गयी है | परीक्षण संकेत देते है की बाग़ के काम-से - काम 250 किग्र फास्फोरिक अम्ल ,कम-से-काम 270 किग्र और क्लोरीन के अधिक -से- अधिक 310 किग्र की आवश्यकता है | यदि उत्पादक बाग़ के लिए मिलाई जाने वाली नाइट्रोजन की मात्रा का न्यून्तमीकरण करना चाहता है तथा प्र्त्येक मिश्रण के कितने थैले का उपयोग होना चाहिए ? मिलाई जाने वाली नाइट्रोजन के निम्नतम मात्रा किया है | lt brgt
 03:28View Solution
03:28View Solutionफलन Z=2x+3y का अधिकतम मान ज्ञात कीजिए जबकि प्रतिबन्ध निम्नलिखित है :
x+2y≤10,2x+y≤14,
x≥0,y≥0.02:16View Solutionमाना A तथा B दो ऐसी घटनाएं हैं कि P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14 तथा P(→A)=14 हैं जबकि →A घटना A के पूरक को दर्शाता हैं, तो घटनाएं A तथा B :
02:32View Solutionlimx→0sin(πcos2x)x2 का मान है ।
03:41View Solutionx+2y≤40,2x+y≤40,x≥0,y≥0
04:46View Solutionx+2y≤100,2x+y≤120,x+y≤70,x≥0,y≥0
04:46View Solutionx+2y≤40,2x+y≤40,x≥0,y≥0
04:50View Solutionरैखिक असमिकाओं के निम्नलिखित निकाय को आलेखीय विधि से हल कीजिए:
x−y≤2,x+y≤4,x≥0,y≥005:55View Solutionनिम्न व्यवरोधों के अन्तर्गत Z=3x+2y का न्यूनतमीकरण कीजिए
x+y≥8,3x+5y≤15 तथा x,y≥005:16View Solutionव्यवरोधों 2x+y≤6,x≤2,x≥0,y≥0के अन्तर्गत Z=11x+7y का अधिकतम मान निर्धारित कीजिए |
05:15View Solutionव्यवरोधों x+y≤1,x≥0,y≥0,y≥0के अन्तर्गत Z=3x+4y का अधिकतमीकरण कीजिए |
05:25View Solutionव्यवरोधों x≤3,y≤2,x≥0,y≥0के अन्तर्गत फलन Z=11x+7y का अधिकतमीकरण कीजिए |
07:46View Solutionनिम्नलिखित असमिकाओं के निकाय के हलों का डोमेन ज्ञात कीजिए :
x≥2,x+2y≤2,x−y+1≤0.05:11View Solutionनिम्न असमिका निकायों को आलेखी विधि से हल कीजिए :
x≥0,y>x,x+y≤9.06:18View Solutionनिम्न असमिका निकायों को आलेखी विधि से हल कीजिए :
x≥0,y≥0,x−y≥0,3x−y+3≤0.08:08View Solutionनिम्न समस्या को हल कीजिए :
Z=6x−2y का अधिकतम मान ज्ञात कीजिए जबकि
2x−y≤2,x≤3,x≥0,y≥004:24View Solution

