एक खिलौना कम्पनी A और B दो प्रकार की गुड़ियों का निर्माण करती है। मार्किट परीक्षणों तथा उपलब्ध संसाधनों से संकेत मिलता है कि सम्मिलित उत्पादन स्तर प्रति सप्ताह 1200 गुड़ियो से अधिक नही होना चाहिए और B प्रकार की गुड़ियों की अधिक से अधिक माँग Aप्रकार की गुड़ियों की आधी है। इसके अतिरिक्त A प्रकार की गुड़ियों का उत्पादन स्तर दूसरे प्रकार की गुड़ियों के उत्पादन स्तर के तीन गुने से 600 नग अधिक है। यदि कम्पनी A और B प्रत्येक गुड़िया पर क्रमशः 12 और 16 का लाभ कमाती है, लाभ का अधि कतमीकरण करने के लिए प्रत्येक के कितने नगों का साप्ताहिक उत्पादन करना चाहिए।
माना A प्रकार की x तथा B प्रकार की y गुड़ियों के उत्पादन का लाभ अधिकतम है।
कम्पनी प्रति गुड़िया ₹ 12 लाभ तथा ₹ 16 लाभ होता है।
rArr "लाभ" Z=12x +16y
x + y का उत्पादन स्तर 1,200 से अधिक नहीं हो सकता है।
x+3y≤1,200
प्रकार के गुड़ियाँ का उत्पादन स्तर प्रकार के गुड़ियों के उत्पादन स्तर के तीन गुने से कम है |
⇒x−3y≤600
B प्रकार की गुड़ियाँ की माँग अधिक से अधिक A प्रकार की गुड़ियों से की माँग की आधी है |
y≤x2
अधिकतम Z=12x+16y
अवरोध है x+y≤1200
x−3y≤600,y≤x2,x,y,≥0
रेखा x+y=1200 बिंदुओं A(1200,0) तथा B(0, 1200) से गुजरती है |
x+y≤1200 में (0,0) रखने पर 0≤1200 जो सत्य है |
अतः x+y≤1200 AB पर या AB के नीचे स्थित है | (ii) रेखा x-3y= 600 बिंदुओं C(600,0) तथा D(0,-200) से गुजरती है | x−3y600 ,में (0,0) रखने पर 0≤600 जो सत्य है | अर्थात x−3y≤600, CD पर और CD के ऊपर स्थित है |
(iii) y=x2 बिंदुओं (800,400) और (0,0) से गुजरती है| x=200 ,y=0 रखने पर 0≤2002 जो सत्य है | अतः (200,0) OP इस क्षेत्र में स्थित है |
(iv) x≥0,y अक्ष पर और उसके दायी ओर स्थित है |
(v) y≥0,x अक्ष पर या उसके ऊपर स्थित है |
छायांकित भाग PQCO घिरे हुए को प्रदर्शित करता है | बिंदु P निम्न रेखाओं का प्रतिच्छेदन बिंदु है |
x+y=1200,y=x2 हल करने पर के निर्देशांक(800,400) है |
बिंदु Q निम्न रेखाओं का प्रतिच्छेद बिंदु है |
x+y=1200
x -3y = 600
घटने पर 4y=600,y=150
तथा x=1200-150= 1050
∴ बिंदु Q(600,0) है
बिंदु C(600,0) है |
उद्देश्य फलन है: z= 12x+16 y
P(800,400) पर, z= 9600 +6400 = 16000
Q(1050,150) पर, Z=12×1050+16×150
= 12600 + 2400 = 15000
C(600,0) पर Z=12×600+0
=7200 +0 = 7200
O(0,0) पर Z=0
⇒P (800,400) पर Z अधिकतम है | Z का अधिकतम मान ₹ 16000 है | इसलिए A प्रकार की 800 गुड़ियों तथा B प्रकार की 400 गुड़ियों पर अधिकतम लाभ है तथा उत्पादन करने में अधिकतम लाभ ₹ 16000 है |

Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - रैखिक प्रोग्रामन EXERCISE - उदाहरण1videos
रैखिक प्रोग्रामन
- BOOK - MANOHAR RAYCHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्नावली 12(A)16videos
रैखिक प्रोग्रामन
- BOOK - MANOHAR RAYCHAPTER - प्रायिकता EXERCISE - इंजीनियरिंग परीक्षाओं के प्रश्न4videos
प्रायिकता
- BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न7videos
सततता तथा अवकलनीयता
Similar Questions
एक फल उत्पादक अपने बाग़ में दो प्रकार के खादों तथा ब्राण्डों का उपयोग कर सकता है मिश्रण के प्र्तेक थैले में नाइट्रोजन ,फास्फोरिक अम्ल , पोटॉश और क्लोरीन की मात्रा (किग्र में ) सारणी में दी गयी है | परीक्षण संकेत देते है की बाग़ के काम-से - काम 250 किग्र फास्फोरिक अम्ल ,कम-से-काम 270 किग्र और क्लोरीन के अधिक -से- अधिक 310 किग्र की आवश्यकता है | यदि उत्पादक बाग़ के लिए मिलाई जाने वाली नाइट्रोजन की मात्रा का न्यून्तमीकरण करना चाहता है तथा प्र्त्येक मिश्रण के कितने थैले का उपयोग होना चाहिए ? मिलाई जाने वाली नाइट्रोजन के निम्नतम मात्रा किया है | lt brgt
 03:59View Solution
03:59View Solutionफलन Z=2x+3y का अधिकतम मान ज्ञात कीजिए जबकि प्रतिबन्ध निम्नलिखित है :
x+2y≤10,2x+y≤14,
x≥0,y≥0.08:56View Solutionमाना A तथा B दो ऐसी घटनाएं हैं कि P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14 तथा P(→A)=14 हैं जबकि →A घटना A के पूरक को दर्शाता हैं, तो घटनाएं A तथा B :
08:58View Solutionlimx→0sin(πcos2x)x2 का मान है ।
View Solutionअभिक्रिया 12A→2B के लिए 'A' के विघटन की दर B' के बनने की दर से निम्न प्रकार सम्बंधित है
01:53View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
42:29View Solutionएक निर्माणकर्ता का मानना है की पुरुष और महिला मजदूरों की दक्षता समान होती है| अतएव वह उन्हें एक ही दर से मजदूरी देता है| उसके पास 30 मात्रक (units ) मजदूर और 17 मात्रक पूंजी है| जिसका वह A और B दो प्रकार के माल के उत्पादन में प्रयोग करते है|A के एक मात्रक उत्पादन में 2 मजदूर और 3 मात्रक पूंजी आवश्यकता है, जबकि B के एक मात्रक उत्पादन में 3 मजदूर और 1 मात्रक पूंजी आवश्यक है| A के एक मात्रक का मूल्य रु 100 तथा B के एक मात्रक का मूल्य रु 120 है | वह अपने साधनो का उपयोग किस प्रकार करें ताकि अधिकतम आय हो? क्या आप निर्माणकर्ता के इस दृष्टिकोण (विचार) से सहमत है की पुरुष और महिला मजदूरों की क्षमता समान होती है अतएव उन्हें एक ही दर से मजदूरी देनी चाहिए?
02:03View Solutionदूध से दही का बनना किस प्रकार के परिवर्तन की श्रेणी में आता है?
01:31View Solutionवर्गीकृत आंकड़ों की 'से कम प्रकार' और 'से अधिक प्रकर' की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के 'भुज' से प्राप्त होता है आंकड़ों का----
02:16View Solutionसजीवों को भोजन की आवश्यकता क्यों होती है ?|भोजन की पूर्ती |फसल |फसल उत्पादन की आवश्यकता क्यों ?|फसलों के प्रकार |Summary
02:22View Solution“पाठ से तीनों प्रकार की संज्ञाओं के उदाहरण खोजकर लिखिए।" अभ्यास प्रश्न का उदाहरण है।
02:22View SolutionThe table shows the production of different types of cars (in thousands). यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है | What is the ratio of the total production of cars of type A in 2014 and type C in 2013 taken together to the total production of cars of type B in 2016 and type E in 2015 taken together? 2014 में A प्रकार की कारों और 2013 में C प्रकार की कारों के कु ल उत्पादन का 2016 में B प्रकार की कारों और 2015 में E प्रकार की कारों के कुल उत्पादन के साथ अनुपात ज्ञात करें |
03:43View SolutionThe table shows the production of different types of cars (in thousands). यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है | The total production of type B cars in 2012, 2014 and 2015 taken together is approximately what percent more than the total production of type A cars in 2013 and 2016 taken together? 2012, 2014 और 2015 में B प्रकार की कारों का कुल उत्पादन 2013 एवं 2016 में A प्रकार की कारों के कुल उत्पादन से लगभग कितना प्रतिशत अधिक है ?
01:47View SolutionThe table shows the production of different types of cars (in thousands). यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है | The number of years, in which the production of cars of type B is less than the average production of type D cars over the years is: कितने वर्ष B प्रकार की कारों का उत्पादन इन वर्षों के दौरान D प्रकार की कारों के औसत उत्पादन से कम रहा है ?
01:47View SolutionThe table shows the production of different types of cars (in thousands)
यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में ) दर्शाती है |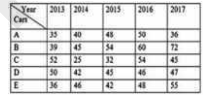 The production of cars of type A in 2015 and of type C in 2013 taken together is approximately what percent of the total production of cars of type D in five years?
The production of cars of type A in 2015 and of type C in 2013 taken together is approximately what percent of the total production of cars of type D in five years?
2015 में A प्रकार की कारों का उत्पादन तथा 2013 में C प्रकार की कारों के उत्पादन को मिला दिया जाए, तो ये पांच वर्षों में D प्रकार की कारों के कुल उत्पादन का लगभग कितना प्रतिशत है ?02:15View SolutionThe table shows the production of different types of cars by a company (in thousands) in 5 years.
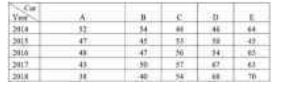 The total production of type B cars in all the five years is what percent more than the total
production of type A, B and D cars in 2017?
The total production of type B cars in all the five years is what percent more than the total
production of type A, B and D cars in 2017?
सभी पांच वर्षों में B प्रकार की कारों का कुल उत्पादन 2017 में A, B और D प्रकार की कारों के कुल उत्पादन से कितना प्रतिशत अधिक है ?02:08View Solution

