पासों के एक जोड़े को तीन बार उछालने पर द्विकों (doubles ) की संख्या का प्रायिकता बंटन ज्ञात कीजिये।
माना X द्विकों की संख्या निरूपित करता है अर्थात (1,1,), (2,3), (3,3), (4,4), (5,5) और (6,6)
स्पष्टयता, X का मान, 0,1,2 या 3 है।
एक द्विक प्राप्त होने की प्रायिकता
एक द्विक प्राप्त न होने की प्रायिकता
अब P(X=0)=P (एक भी द्विक नहीं) =
(एक द्विक और दो द्विक नहीं)
P(X=2)=P (दो द्विक और एक द्विक-नहीं)
.
(तीन द्विक)=
अतः अभ्यस्त प्रायिकता बंटन
सत्यापन : प्रायिकताओं का योग
अतः उपरोक्त बंटन सही है।
Topper's Solved these Questions
- प्रायिकता Book:MANOHAR RAYChapter:प्रायिकता Exercise:प्रश्नावली 13(A)
Explore 27 Videos
- प्रायिकता Book:MANOHAR RAYChapter:प्रायिकता Exercise:प्रश्नावली 13(B)
Explore 22 Videos
- प्रतिलोम त्रिकोणमितीय फलन Book:MANOHAR RAYChapter:प्रतिलोम त्रिकोणमितीय फलन Exercise:प्रश्नावली 2(C)
Explore 17 Videos
- रैखिक प्रोग्रामन Book:MANOHAR RAYChapter:रैखिक प्रोग्रामन Exercise:प्रश्नावाली 12 (C) दीर्घ उत्तरीय प्रश्न
Explore 4 Videos
Similar Questions
यदि P(A)=38,P(B)=58 और P(A∩B)=34, तो P(AB) तथा P(BA) का परिकलन कीजिए |
View Solutionदो स्वतंत्र घटनाओं A तथा B की प्रायिकता क्रमश : P(A)=−0.40 तथा P(B)+0.50 है, तो निम्नलिखित के मान ज्ञात कीजिए -
(i) P(AB)
(ii) P(A, B-नहीं)
(iii) P( A-नहीं, B)
(iv) P(A-नहीं, B-नहीं)
View Solutioncos−1(cos7π6) का मान होगा
View Solutionएक किसान दो प्रकार के चारे P और Q को मिलाता (मिश्रण) है। P प्रकार के चार, जिसका गूल्य Rs 250 प्रति थैले जोकि पोषक तत्व के 3 मात्रक, तत्व B के 2.5 मात्रक और तत्य C के 2 माक रखता है जबकि Q प्रकार का चार जिसका मूल्य Rs 200 प्रति थैला है, पोषक तत्व A का 1.5 मात्रक, तत्व B का 11.25 मात्रक और तत्व C के तीन रखता है। पोषक तत्वों A, B और C की न्यून्तम आतश्यताएँ 18 मात्रक, 45 मात्रक और 24 मात्रक है। प्रत्येक प्रकार के थैले की सांख्या ज्ञात कीजिए ताकि मिश्रण के प्रत्येक थैले का मूल्य न्यूनतम हो ? मिश्रण के प्रत्येक वेले का न्यूनतम मूल्य कथा है?
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - 4 सफलता के लिए
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionदो पासो को एक साथ चार बार फेका जाता है दोनों पासो पर प्राप्त अंको का योग 7 कम से कम दो बार आने की प्रायिकता ज्ञात कीजिए
View Solutionएक पासा 5 बार फेका जाता है यदि विषम संख्या प्राप्त होने को के सफलता माना जाए तो प्रायिकता ज्ञात कीजिए - चार सफलताएं प्राप्त हो
View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
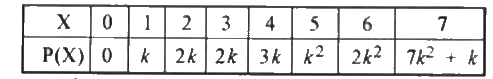 ज्ञात कीजिये-
ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)
View Solutionपासों के एक जोड़े को 7 बार फेंका गया है। यदि 'पासों पर प्राप्त अंकों का योग 7 होना' सफलता मनी जाती तो क्या प्रायिकता है-
(i) कोई साफलता नहीं
(ii) छ: सफ्ल्तएन
(iii) कम से कम छ: सफलताएँ
View Solutionएक व्यक्ति के लक्ष्य भेदन की प्रायिकता 1/4 है। वह कम से कम कितनी बार गोली चलाये कि लक्ष्य को कम से कम एक बार भेदने की प्रायिकता 2/3 से अधिक हो?
View Solutionयदि एक निष्पक्ष सिक्के को 20 बार उछला जाता है और मान लीजिये कि n बार शीर्ष दिखाई देता है, तो n के विषम होने की प्रायिकता का मान ज्ञात कीजिए।
View Solutionयदि एक न्याय्य सिक्के को 10 बार उछला जाता है, ठीक चार पट आने की प्रायिकता ज्ञात कीजिए।
View Solutionएक पासे को 7 बार उछालने पर तथ्यतः दो बार 5 आने कि प्रायिकता ज्ञात कीजिए ।
View Solutionएक व्यक्ति के लक्ष्य भेदन की प्रायिकता 14 है। यह कम - से - कम कितनी बार गोली चलाए की लक्ष्य को कम से कम एक बार भेदने की प्रायिकता 23 से अधिक हो ?
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solution
