यदि (2+a)50 के द्विपद प्रसार का सत्रहवाँ और अठारहवाँ पद समान हो, तो a का मान ज्ञात कीजिए ।
1
2
3
4
The correct Answer is:A
r + 1 वां पद Tr+1 से प्रकट करे, तब
Tr+1=.nCr.xn−r.Ar
17 वे पद के लिए (2+a)50 के द्विपद प्रसार में,
T16+1=.50C16.(2)50−16.(a)16
T17=50!34!16!.(2)34.a16
इसी प्रकार (2+a)50 के द्विपद प्रसार में 18 वां पद
T17+1=.50C17.(2)50−17.(a)17
T18=50!33!.17!.(2)33.a17
प्रश्नानुसार दोनों पद समान हैं, तब
T18−T17
50!33!.17!.(2)33.a17=50!34!.16!.(2)34.a16
a17a16=50!34!.16!×33!.17!50!.(2)34(2)33
a17−16=33!×17×16!34×33!×16!×(2)34−33
a=1734×2
a = 1.
Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - द्विपद प्रमेयEXERCISE - प्रश्नावली 8(A)18videos
द्विपद प्रमेय
- BOOK - MANOHAR RAYCHAPTER - द्विपद प्रमेयEXERCISE - प्रश्नावली 8(B)22videos
द्विपद प्रमेय
- BOOK - MANOHAR RAYCHAPTER - त्रिविमीय ज्यामिति का परिचय EXERCISE - प्रश्नावली 12(D)13videos
त्रिविमीय ज्यामिति का परिचय
- BOOK - MANOHAR RAYCHAPTER - प्रायिकता EXERCISE - प्रश्नावली 16(F)18videos
प्रायिकता
Similar Questions
(x+a)26 के प्रसार में कुल पदों की संख्या ज्ञात कीजिए ।
02:53View Solutionगुणांक ज्ञात करो -
(A) (x3−1x3)12 के प्रसार में x12 का |
(B) (2x3−13x3)10 के प्रसार में x5 का |
(C) (x+3)8 के प्रसार में x5 का |
(D) (x3−1x4)10 के विस्तार में x9 का |
(E) (x2+ax) के विस्तार में x18 का |
(F) (x−1x2)2 के प्रसार में 1x का |05:31View Solutionx - अक्ष पर स्थित किसी बिंदु के निर्देशांक है
02:29View Solution52 ताशों की गड्डी में से 3 ताश खींचे जाते हैं। प्रायिकता ज्ञात कीजिए कि तीनों ताश बादशाह होंगे।
02:59View Solution→a और →b असंरेख है |यदि सदिश →α=(x−2)→a+→b और →β=(3+2x)→a−2→b संरेख सदिश हो तो x का मान ज्ञात कीजिए|
02:58View Solutionयदि 3+5r+7r2+……..∞=449 हो ,तो r का मान ज्ञात कीजिए ।
01:40View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
01:44View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
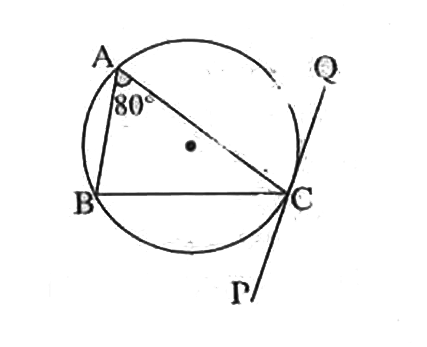 View Solution
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=(2x−1)2+304:18View Solutionनिम्नलिखित फलनों के अधिकतम था निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
|sin4x+3|04:46View Solutionनिम्नलिखित फलनों के अधिकतम था निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
sin2x+502:33View SolutionZn की एक छड़ के विलयम में डूबी हुई है यदि E_(zn^(+2)//(zn))^(0) = -0.76 V हो और ताप 298 K हो तो Znइलेक्ट्रोड का विभव ज्ञात कीजिए
03:00View Solutionयदि (1+xlog2x)5 के द्विपद प्रसार में तीसरा पद 2560 के बराबर है, तो x का एक सम्भव मान है
03:00View Solution(1) किसी A.P. के प्रथम 10 पदों का योगफल ज्ञात कीजिए यदि T1=−14 और T5=20.
(ii) किसी A.P. का तीसरा पद 14 और 8वाँ पद 34 है।Sn और S30 ज्ञात कीजिए।03:00View Solutionयदि f:R→R,f(x)=x2−5x+4 तो fof का मान ज्ञात कीजिए।
02:13View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
05:33View Solution

