एक गेंद जिसका द्रव्यमान 1 ग्राम है तथा जिस पर 10−8 कूलॉम आवेश है, एक बिंदु से दूसरे बिंदु की ओर चलती है। यदि पहले बिंदु का विभव 600 वोल्ट हो तथा दूसरे बिंदु का विभव शून्य हो तथा दूसरे बिंदु पर गेंद का वेग 20 सेमी/सेकंड हो, तो पहले बिंदु पर गेंद का वेग क्या होगा ?
माना पहले बिंदु पर गेंद का वेग v1 तथा दूसरे बिंदु पर वेग v2 है। इन बिंदुओ पर विभव क्रमशः V1 व V2 है।
प्रश्नानुसार, m = 1 ग्राम =10−3 किग्रा, q=10−8 कूलॉम, V1=600 वोल्ट, V2=0,
v2=20 सेमी/सेकंड =20×10−2 मीटर/सेकंड, v1=?
गतिज ऊर्जा में वृद्धि = किया गया कार्य
12mv21−12mv22=q(V1−V2)
अथवा 12×10−3[v21−(20×10−2 मीटर/ Second2]
=10−8 कूलॉम ×600 वोल्ट =6×10−6 जूल
अथवा v21−400×10−4=12×10−3
अथवा v21=4×10−2+1.2×10−2
=5.2×10−2m2Second2
thereoev1=√5.2×10−2=2.28×10−1 मीटर/सेकंड
=(2.28×10−1)×102 सेमी/सेकंड
=22.8 सेमी/सेकंड ।
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - वैधुत विभव EXERCISE - प्रश्नावली23videos
वैधुत विभव
- BOOK - NOOTAN HINDICHAPTER - वैधुत विभव EXERCISE - अतिलघु उत्तरीय29videos
वैधुत विभव
- BOOK - NOOTAN HINDICHAPTER - वैधुत फ्लेक्स तथा गौस की प्रमेय EXERCISE - वस्तुनिष्ठ प्रकार प्रशन23videos
वैधुत फ्लेक्स तथा गौस की प्रमेय
- BOOK - NOOTAN HINDICHAPTER - व्यतिकरण EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न23videos
व्यतिकरण
Similar Questions
वैद्युत विभव का मात्रक है -
03:05View Solutionवैधुत विभव की परिभाषा बताइए तथा इसकी विमा लिखिए
03:29View SolutionL मीटर भुजा का वर्गाकार शेरेस्ट कागज के टेल में है एक एकसमान विधुत क्षेत्र ˆE वाल्ट/कॉलम भी कागज के तेल में वर्गाकार शेरेस्ट के निचे के आधे भाग में सीमित है SI मात्रक में षेरेस्ट से सम्भंदित विधुत फ्लेक्स है
 03:01View Solution
03:01View Solutiony1=asin(ωt–kt) तथा y2=acos(ωt–kx) से व्यक्त दो प्रगामी तरंगे अध्यारोपित होती है। x पर परिणामी तरंग की आयाम होगा:
02:52View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
04:45View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
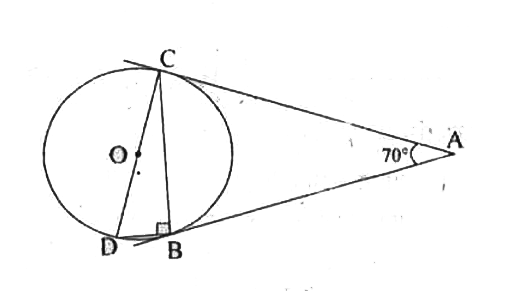
04:21View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
 03:38View Solution
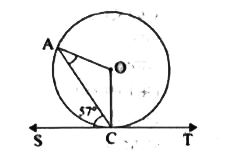
03:38View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
 04:33View Solution
04:33View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
06:02View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
03:44View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
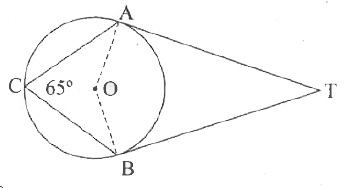
03:59View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
 03:53View Solution
03:53View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -
 05:40View Solution
05:40View Solutionमाना O(0,0) तथा A(0,1) दो निश्चित बिंदु है, तो ऐसे बिंदु P जिनके लिए ΔAOP का परिमाप 4 हो, का बिन्दुपथ है
01:23View Solutionएक बिंदु P,2x−3y+4=0 पर गति करता है । यदि Q(1,4) तथा R(3,-2) निश्चित बिंदु है, तो ΔPQR के केन्द्रक का बिन्दुपथ (locus) एक रेखा है
01:50View Solutionबिंदु (3,4,5) से समतल x+y+z=9 पर डाले गए लम्ब का पाद बिंदु होगा
01:06:54View Solution

