2 किग्रा द्रव्यमान का एक गुटका क्षैतिज से 30° के कोण पर झुके हुए एक नत समतल पर रखा हैं | गुटके और तल के मध्य घर्षण गुणांक हैं |
( i ) तल पर नीचे की ओर अत्वरित गति के लिए गुटके पर कितना बल लगाना होगा ?
( ii ) तल पर ऊपर की ओर अत्वरित गति के लिए गुटके पर कितना बल लगाना होगा ?
(iii) यदि गुटका दोनों ही स्थितियों में एकसमान चाल से गति करता हैं तो गुटके पर लगी शक्तियों का अनुपात ज्ञात कीजिये |
(i) जब गुटका नीचे की ओर चलता है तब गुटके पर लगने वाले बल है: इसका भार mg उर्ध्वाधरत: नीचे की ओर, अभिलम्ब प्रतिक्रिया-बल R, गतिज घर्षण-बल गति के विपरीत दिशा में (ऊपर को), गुटके पर के अनुदिश नीचे की ओर लगाया गया बल F
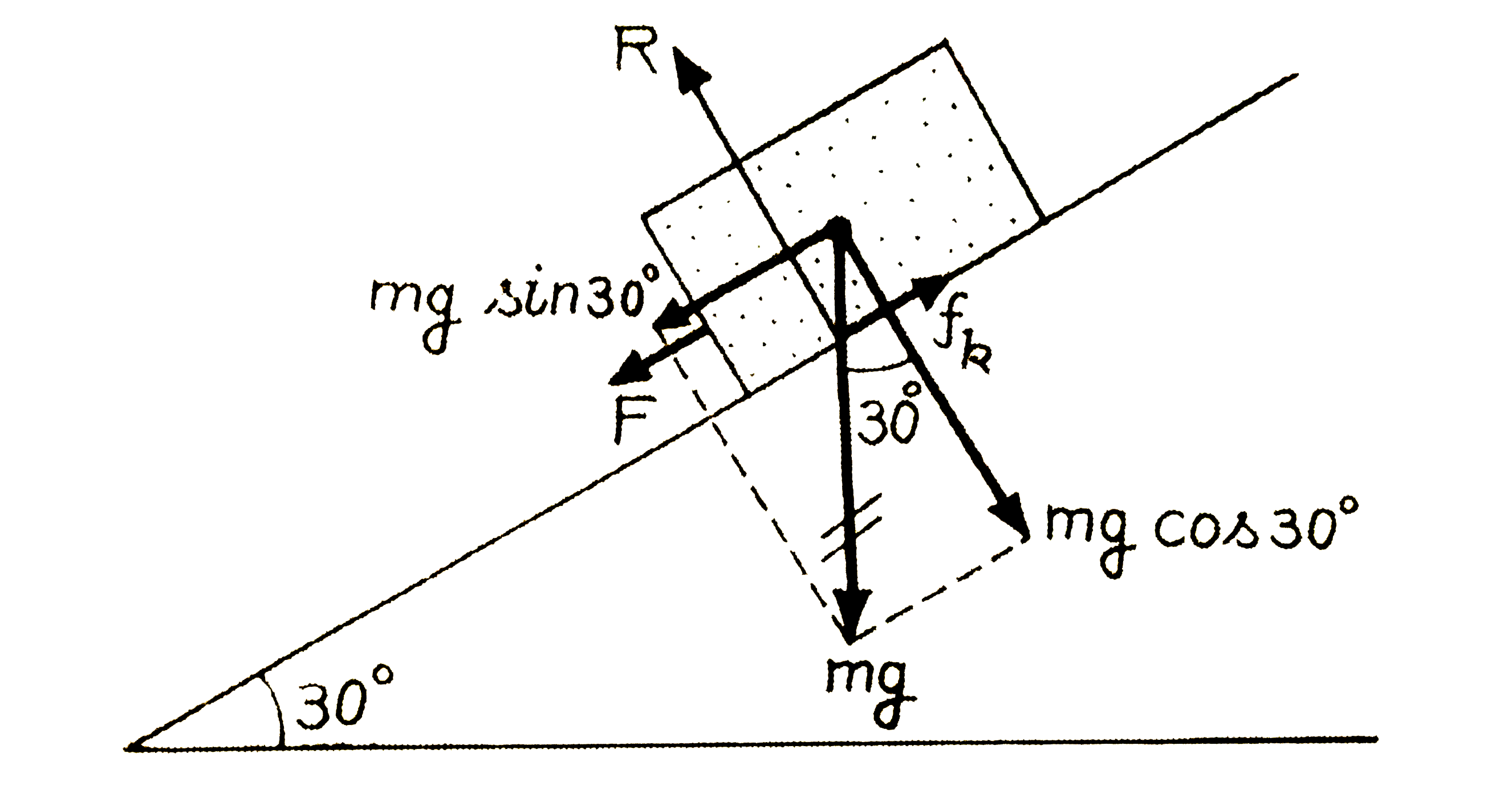
भार mg के दो घटको में वियोजित कर सकते है: तल के समांतर घटक तथा तल के लंबवत घटक गुटके पर तल के समांतर (नीचे को) लगने वाला नेट बल है। बिना त्वरण गति के लिये यह शून्य होगा:
....(i)
चित्रानुसार (चूँकि तल के लम्बवत कोई गति नहीं है) तथा घर्षण-बल
अत: समीकरण (i) से
अथवा
दिये गये मान रखने पर
F = 2 किग्रा न्यूटन/किग्रा
= 9.8 न्यूटन न्यूटन।
(ii) ऊपर की ओर बिना त्वरण गति के लिये गुटके पर बल F संलग्न चित्र में प्रदर्शित है। अब घर्षण -बल नीचे को दिष्ट होगा।
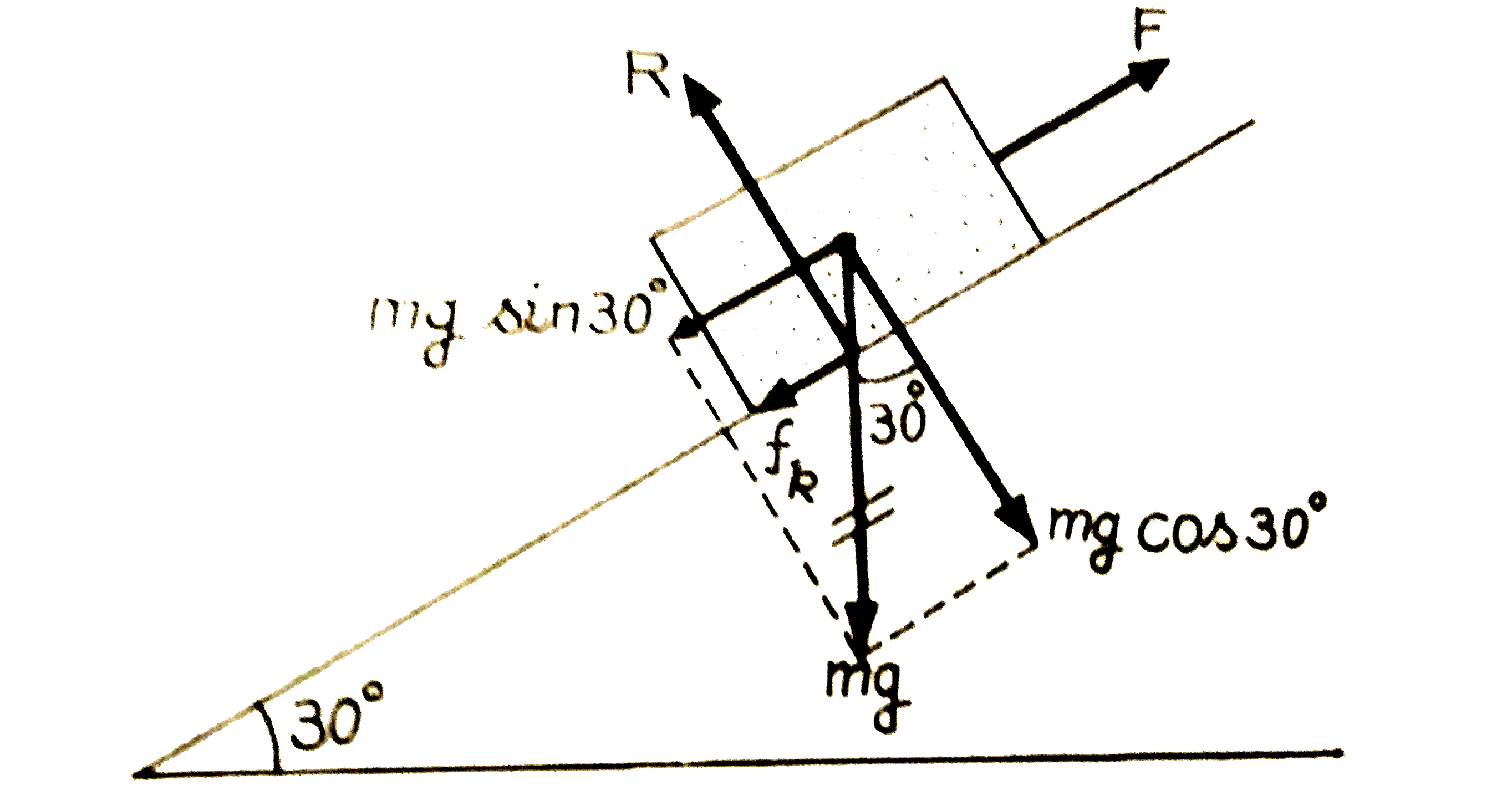
पुन: गुटके पर तल के समांतर (ऊपर को) नेट बल शून्य होगा:
अनुच्छेद (i) की भाँति
ltbr) न्यूटन।
Topper's Solved these Questions
- घर्षण BOOK - NOOTAN HINDICHAPTER - घर्षण EXERCISE - वस्तुनिष्ठ प्रश्न
11 Videos
- घर्षण BOOK - NOOTAN HINDICHAPTER - घर्षण EXERCISE - अतिलघु उत्तरीय
20 Videos
- कार्य, शक्ति एवं ऊर्जा BOOK - NOOTAN HINDICHAPTER - कार्य, शक्ति एवं ऊर्जा EXERCISE - अतिरिक्त प्रश्न
7 Videos
- तरंग गति BOOK - NOOTAN HINDICHAPTER - तरंग गति EXERCISE - एन सी ई आर टी प्रश्न (अतिरिक्त प्रश्न)
6 Videos
Similar Questions
सम्पर्क में रखे दो तलो के बीच महत्तम स्थैतिक घर्षण है। वे तल है:
View Solutionसीमांत घर्षण से आप क्या समझते है?
View Solution0.012kg द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है । गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए ।
View Solutionचित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ काट का क्षेत्रफल a है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए की गई जब गोली को थोड़ा दबाकर मुक्त छोड़ा देते है, तो वह सरल आवर्त गति करती है। दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यजंक ज्ञात कीजिए [चित्र देखिए]।
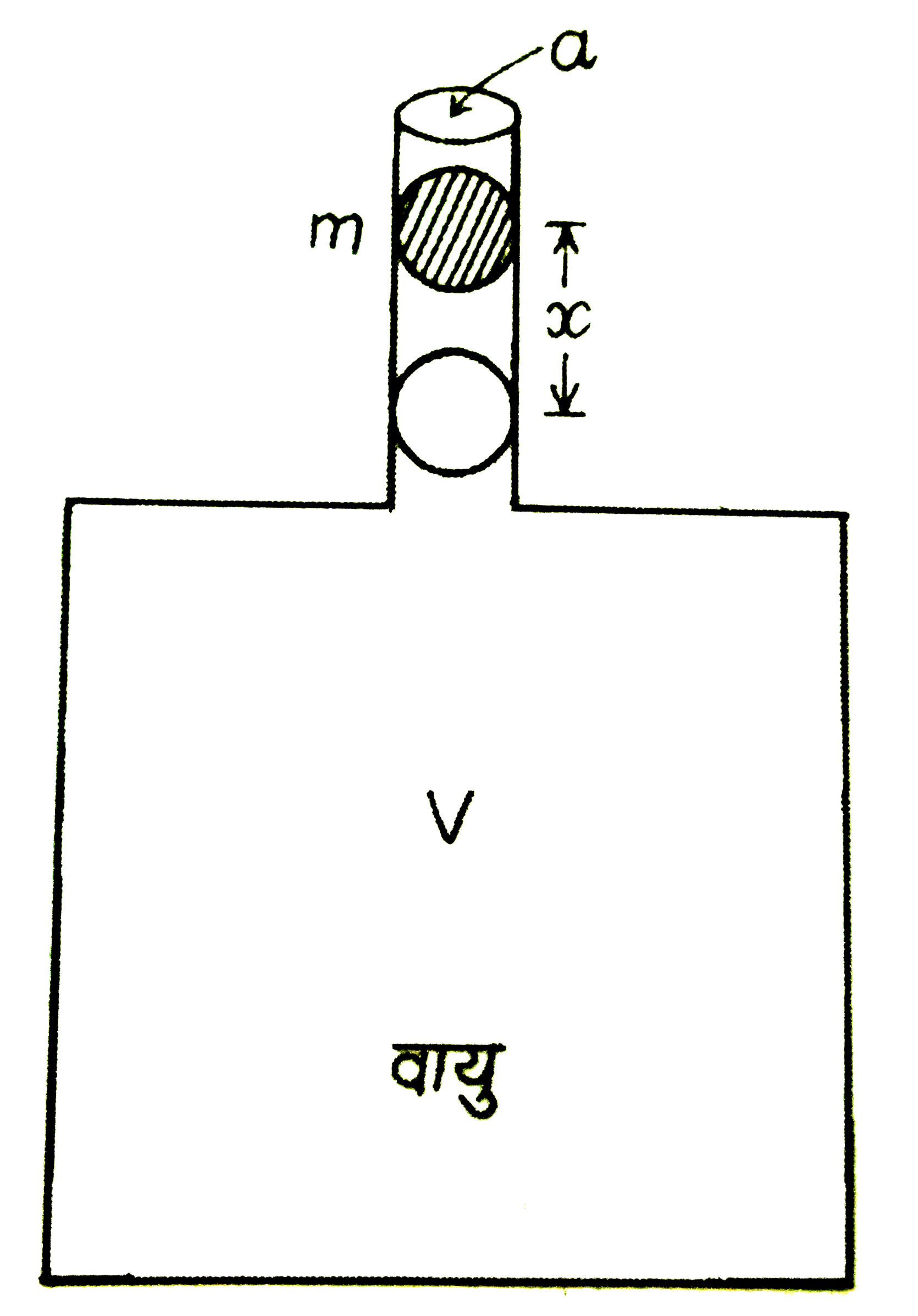
View Solutionआनत तल पर वस्तु की गति
View Solutionआनत घर्षण वाले तल पर वस्तु की गति -1
View Solutionआनत घर्षण वाले तल पर वस्तु की गति -2
View Solutionघर्षण कोण | समतल सतह पर वस्तु की गति | आनत तल पर वस्तु की गति
View Solutionघर्षण रहित नत तल पर रखे गुटके की गति
View Solutionघर्षण रहित नत तल पर रखे गुटकों की गति
View Solutionनत तल पर घर्षण
View Solutionबल तथा गति के नियम पर प्रश्न
View Solutionनत तल पर लौटनी गति #!#महत्वपूर्ण उधारण
View Solutionएक कोण पर झुके हुए तल पर ऊँचाई से प्रक्षेप्य
View Solutionदो अनन्त लम्बाई के समान्तर तार जिन पर रेखीय आवेश घनत्व क्रमश: λ1, औरλ2 , हैं R मीटर की दूरी पर रखे हैं, उनमें से किसी एक की एकांक लम्बाई पर बल होगा
View Solutionआनत तल पर गति
View Solution
