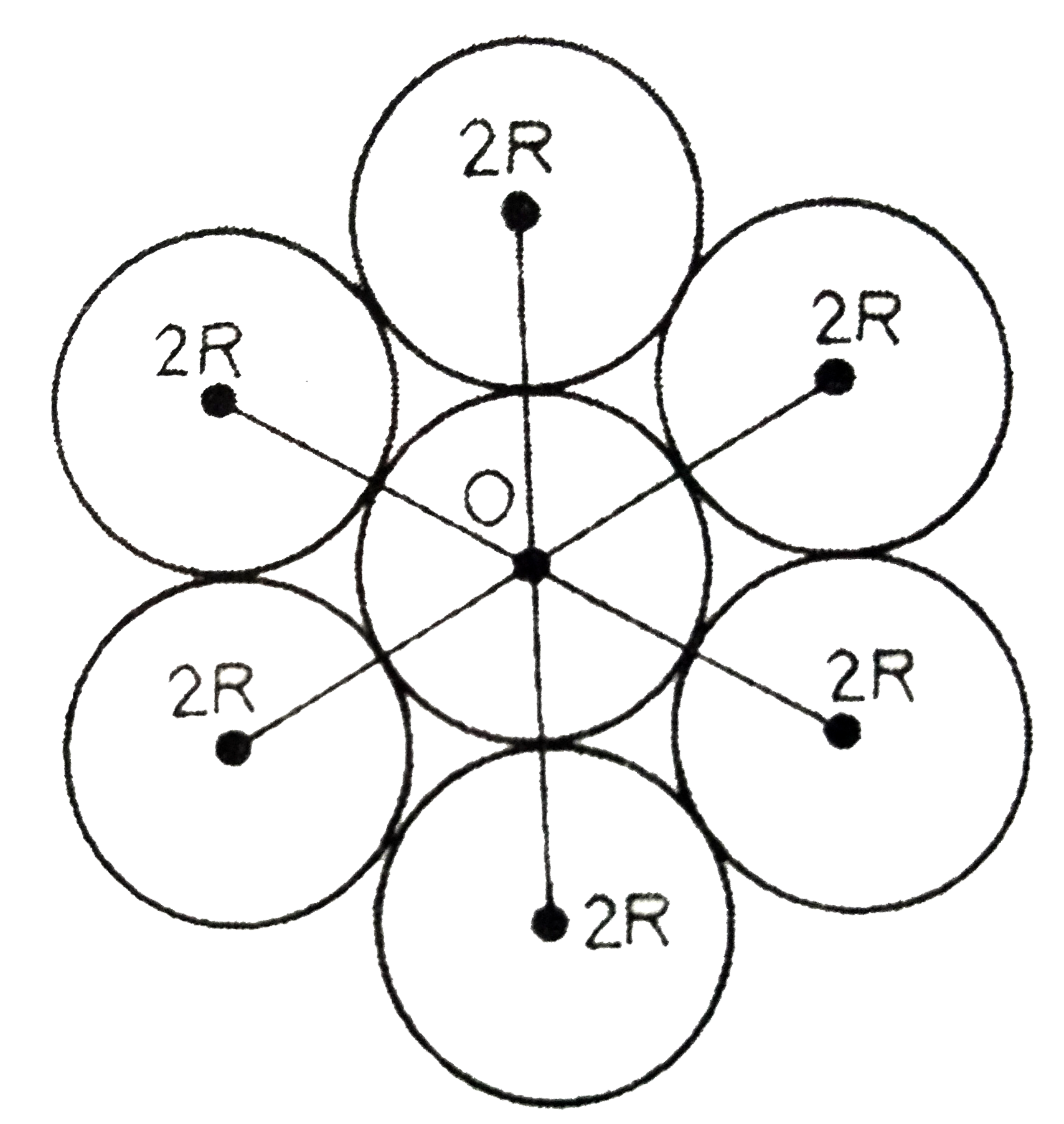
चित्रानुसार सात एक जेकसी वृत्ताकार समतल डिस्कों, जिनमें प्रत्येक का द्रव्यमान M तथा त्रिज्या R है को सममित रूप से जोड़ा जाता है। समतल के लम्बवत तथा P से गुजरने वाली अक्ष के सापेक्ष इस संयोजन का जड़त्व आघूर्ण है:
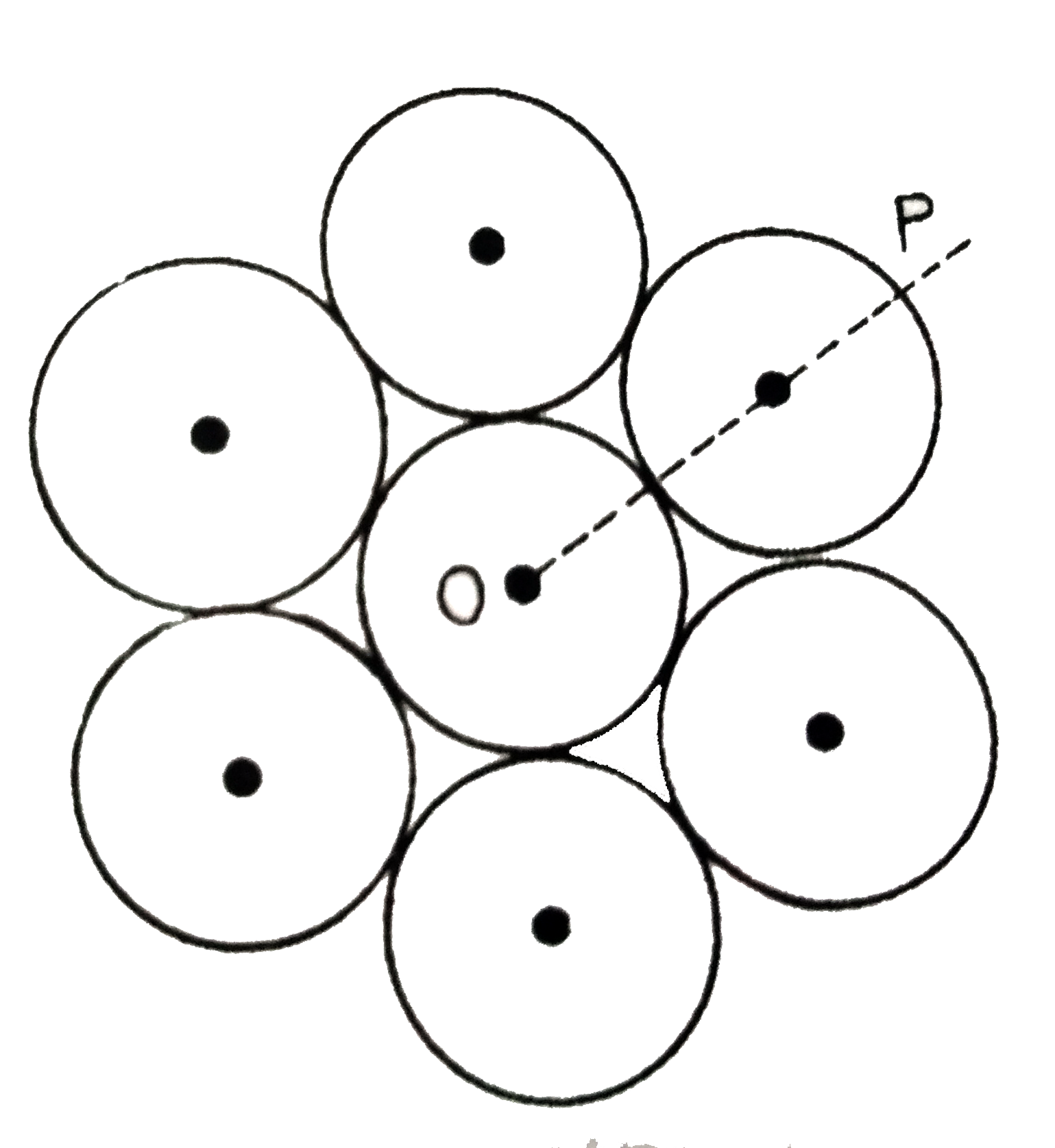
552MR2
732MR2
1812MR2
192MR2
IO=Icm+md2
=7MR22+[6M×(2R)2]
=55MR22
IP=IO+md2
=55MR22+7M(3R)2
=1812MR2
Topper's Solved these Questions
- दृढ़ पिण्डों की घूर्णन गति BOOK - NOOTAN HINDICHAPTER - दृढ़ पिण्डों की घूर्णन गति EXERCISE - एन. सी. ई. आर. टी. प्रश्न
21 Videos
- दृढ़ पिण्डों की घूर्णन गति BOOK - NOOTAN HINDICHAPTER - दृढ़ पिण्डों की घूर्णन गति EXERCISE - एन. सी. ई. आर. टी. अतिरिक्त प्रश्न
11 Videos
- दृढ़ पिण्डों की घूर्णन गति BOOK - NOOTAN HINDICHAPTER - दृढ़ पिण्डों की घूर्णन गति EXERCISE - प्रश्नावली (आंकिक)
26 Videos
- तीन डोरियों के कम्पन : स्वरमापी BOOK - NOOTAN HINDICHAPTER - तीन डोरियों के कम्पन : स्वरमापी EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
11 Videos
- दोलन अथवा कम्पन BOOK - NOOTAN HINDICHAPTER - दोलन अथवा कम्पन EXERCISE - प्रश्नावली (दीर्घ उत्तरीय )
9 Videos
Similar Questions
एक समान द्रव्यमान घनत्व के निम्नलिखित पिण्डों में प्रत्येक के द्रव्यमान-केंद्र की अवस्थिति लिखिएः
a. गोला b. सिलिण्डर c.छल्ला तथा d घन
View Solutionजैसा चित्र में दिखाया गया है एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगा कर जोड़ा गया है। इन्हें ठीक बचल में 0.5m लम्बी रस्सी है। सीढ़ी BA के अनुदिश B से 1.2m की दूरी पर स्थित बिंदु F से 40kg का एक भार लटकाया गया है। यह मानते हुए कि फर्श घर्षण रहित है और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए। (g=9.8m/s2 लीजिए)

View Solutionएक पहिया जो विरामावस्था में है 3.0radian/second2 के कोणीय त्वरण के अंतर्गत 2.0 सेकण्ड तक घूमता हैं इस समयान्तराल में पहिया कितना कोणीय वेग अर्जित कर लेगा तथा उसमें कितना विस्थापन होगा?
View Solutionहुक के नियम का पालन करने वाली डोरी का विस्तार x है। इस विस्तारित डोरी में ध्वनि की चाल v है। यदि विस्तार बढ़ाकर 1.5 x कर दिया जाये, तो डोरी में ध्वनि की चाल होगी :
View Solutionमुक्त दोलनों से आप क्या समझते हैं? उदाहरण देकर समझाइए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionउस समतल का समीकरण ज्ञात कीजिए, जो अक्षों से समान अन्तःखण्ड काटता है तथा बिंदु (2, 3, 4) से होकर जाता है |
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View SolutionY - अक्ष के समीकरण का सममित रूप …………. है।
View SolutionZ- अक्ष के समीकरण का सममित रूप …………….. है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
View Solution
