एक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है। इससे R/2 त्रिज्या का एक गोलीय भाग, आरेख गये अनुसार काट लिया जाता है। r=∞ (अन्नत) पर गुरुत्वीय विभव के मान V को शून्य (V=0) मानते हुए, इस प्रकार बने कोटर (कैविटी) के केन्द्र पर, गुरुत्वीय विभव का मान होगा : (G = गुरुत्वीय स्थिरांक है)

−GM2R
−GMR
−2GM3R
−2GMR
The correct Answer is:B
सम्पूर्ण ठोस गोले के कारण दूरी पर विभव
V=−GM(3R2−r22R3)
r=R2 पर, V1=−GM⎡⎢
⎢⎣3R2−(R24)2R3⎤⎥
⎥⎦=−118GMR

हटाये गये गोले के कारण कैविटी के केन्द्र P पर विभव
V2=−32×G(−M/8)R/2=38GMR
द्रव्यमान M/8 से पहले ऋण चिन्ह इस कारण लिया गया है क्योकि इसे हटाया गया है। अतः शेष भाग के कारण बिन्दु P पर नैट विभव
V=V1+V2=−118GMR+38GMR=−GMR
Topper's Solved these Questions
Similar Questions
किसी ग्रहो से सूर्य की औसत दूरी, पृथ्वी से सूर्य की औसत दूरी की तुलना में 9 गुनी है। ग्रह का परिक्रमण-काल ज्ञात कीजिए।
View Solutionएक कण का विस्थापन x=0.2(cos2πt2−sin2πt2) मीटर है कण की गति -
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionयदि किसी गोले का समीकरण x2+y2+z2+2ux+2vy+2wz+d=0 है, तो गोले के केन्द्र का निर्देशांक तथा त्रिज्या क्या होगी?
View Solutionगुरुत्वीय त्वरण का मान ज्ञात करना
View Solutionगुरुत्वीय त्वरण के मान का प्रयोग प्रश्नों में | भाग 1
View SolutionIf the value of gravitational acceleration on the earth plane 10 मीटर/ Second ^ 2 है तो इसका मान प्रथ्वी के केन्द्र पर क्या होगा ( यदि प्रथ्वी को R त्रिज्या एंव एकसमान घनत्व का गोला मान लिया जाये)
View Solution300 पर एक अभिक्रिया के लिए साम्य स्थिरांक 10 है| DeltaG^(ө) का मान क्या होगा ? R=8.314 JK^(-1) "mol"^(-1)
View Solutionगुरुत्वीय विभव
View Solutionगुरुत्वीय विभव
View SolutionA copper wire of radius 0.5 mm and length 4223 m is melted and converted into a sphere of radius R cm. What is the value of R?
त्रिज्या 0.5 mm और लंबाई 4223 मी वाले एक ताम्बे के तार को पिघलाकर त्रिज्या R सेमी वाले एक गोले का रूप दिया जाता है |R का मान क्या है ?
View Solutionगुरुत्वीय स्थितिज उर्जा #!#गुरुत्वीय विभव
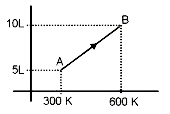
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
View Solutionएक एकपरमाण्विक वास्तविक गैस का एक मोल समीकरण p (V — b) = RT को संतुष्ट करता है जहाँ b एक स्थिरांक है। गैस के लिए अंतरापरमाणुक विभव V(r) और अंतरापरमाणुक दूरी r का संबंध निम्नानुसार दर्शाया जाता है
View Solution
