यदि किसी कृत्रिम उपग्रह का पृथ्वी के ठीक ऊपर चक्कर लगाने का परिक्रमण - काल T है तथा पृथ्वी का घनत्व ρ है, तो सिद्ध कीजिए कि ρT2 सार्वत्रिक नियतांक है | इस नियतांक का मान भी बताइए | (G=6.67×10−11 मीटर 3/ किग्रा - सेकण्ड 2)
यदि किसी उपग्रह का पृथ्वी के चारो ओर का परिक्रमण - काल T है, तब
T2=4π2(Re+h)3/GMe
जहाँ h उपग्रह की पृथ्वी - तल से ऊँचाई है |
∴Me=4π2(Re+h)3GT2
उपग्रह, पृथ्वी के ठीक ऊपर चक्कर लगा रहा है, अतः h उपेक्षणीय है |
∴Me=4π2R3eGT2
परन्तु Me=43πR3eρ, जहाँ ρ पृथ्वी का घनत्व है | इस प्रकार 4π3R3eρ=4π2R3eGT2 अथवा ρT2=3π/G
जो कि सार्वत्रिक नियतांक है | इसका मान ज्ञात करने के लिये
ρT2=3πG=3×3.146.67×10−11 मीटर 3/(किग्रा - सेकण्ड2)
=1.41×1011 किग्रा - सेकण्ड 2 / मीटर 3 |
Topper's Solved these Questions
- उपग्रहों की गति : पलायन वेग BOOK - NOOTAN HINDICHAPTER - उपग्रहों की गति : पलायन वेग EXERCISE - प्रश्नावली ( वस्तुनिष्ठ प्रश्न )
27 Videos
- उपग्रहों की गति : पलायन वेग BOOK - NOOTAN HINDICHAPTER - उपग्रहों की गति : पलायन वेग EXERCISE - प्रश्नावली ( अतिलघु उत्तरीय )
19 Videos
- आदर्श गैस का व्यव्हार तथा अणुगति सिद्धान्तBOOK - NOOTAN HINDICHAPTER - आदर्श गैस का व्यव्हार तथा अणुगति सिद्धान्तEXERCISE - एन. सी. ई. आर. टी. प्रश्न
14 Videos
- उष्मागतिकी BOOK - NOOTAN HINDICHAPTER - उष्मागतिकी EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
15 Videos
Similar Questions
एक उपग्रह पृथ्वी ( त्रिज्या Re ) के अति समीप वृत्तीय कक्षा में परिक्रमण कर रहा है | इसका कक्षीय वेग है :
View Solutionएक ग्रह सूर्य के परितः v मी / से की चल से T सेकण्ड में एक पूरा चक्कर लगता है | दिखाइए कि इस ग्रह का सूर्य की ओर दिष्ट त्वरण का मान 2πvT होता है |
View Solutionऑकसीजन के अणुओं के आयतन और NTP पर इनके द्वारा घेरे गए कुल आयतन का अनुपात ज्ञात कीजिए। ऑक्सीजन के एक अणु का व्यास 3Å लीजिए।
View Solutionएक निश्चित द्रव्यमान की गैस अवस्था A से B तक तीन पथों 1,2 व 3 के द्वारा प्रसारित की गयी है । यदि इन पथों के अनुदिश गैस द्वारा किये गये कार्य क्रमशः W1,W2 तथा W3 है , तब :
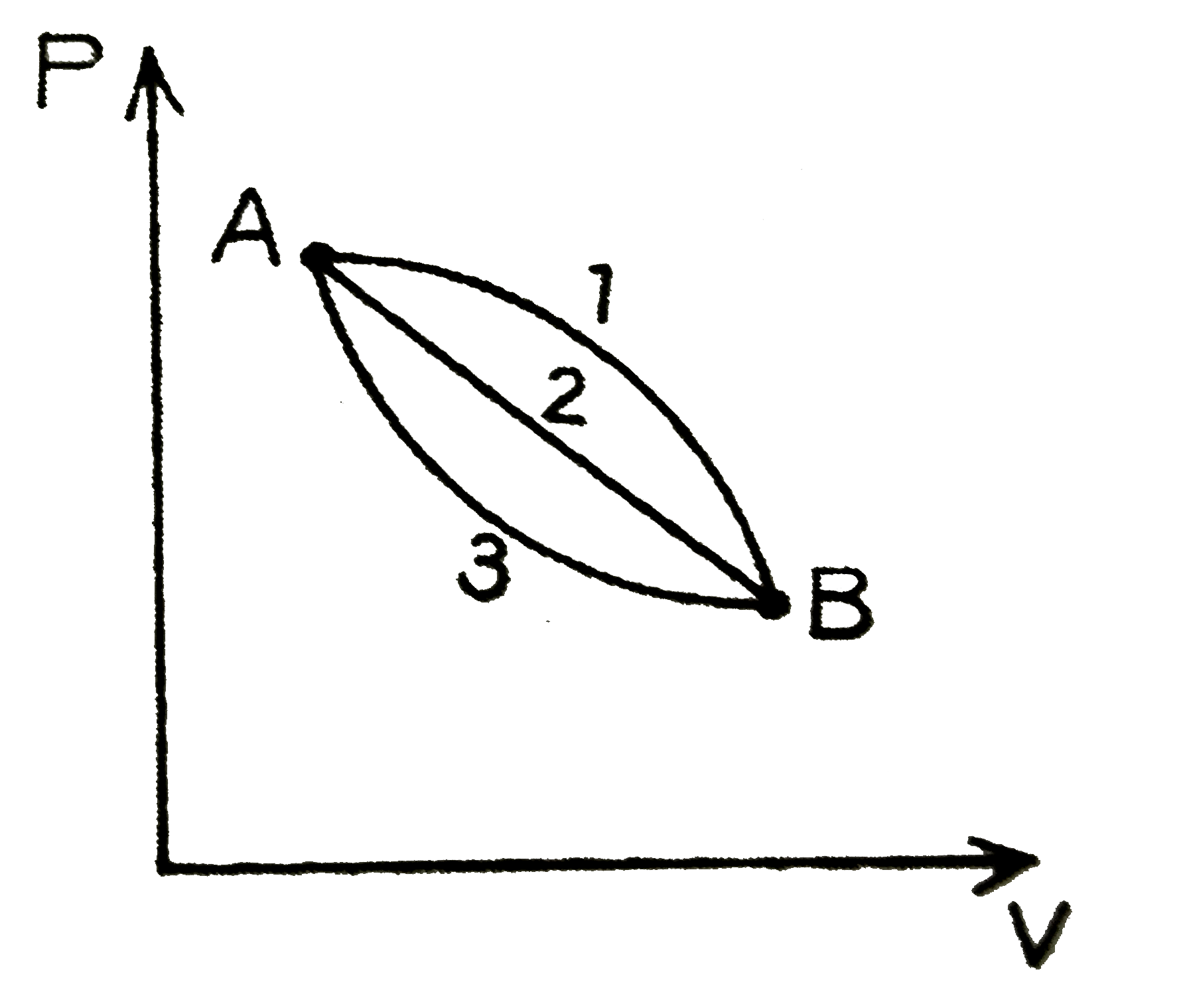
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
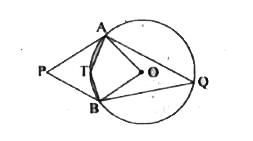
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionयदि z = x + iy हो, तो |z| का मान …………. है ।
View Solutionएक बहुविकल्पीय प्रश्न का उत्तर देने में विद्यार्थी या तो प्रश्न का उत्तर जानता है या जानता लगाता है | मान ले कि उसके उत्तर जान ने कि प्रायिकता 35 है तथा अनुमान लगाने कि प्रायिकता 25 है | मान ले कि छात्र के प्रश्न का उत्तर अनुमान लगाने पर सही उत्तर देने कि प्रायिकता 13 है , तो इसकी क्या प्रायिकता है कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है ?
View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
View Solutionयदि फलन f (x) आवर्त का सतत फलन है , तो समाकलन I=∫a+Taf(x)dx का मान है
View Solutionयदि sinθ=12 तथा θ एक अधिक कोण है , तो cotθ का मान होगा
View Solutionपृथ्वी और चन्द्रमा का कुल द्रव्यमान 6.04×1024 किग्रा है। यदि चन्द्रमा का द्रव्यमान 7.34×1022 किग्रा है तो पृथ्वी का द्रव्यमान ज्ञात कीजिए।
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solutionगुरुत्वाकर्षण|उपग्रह का परिक्रमण काल #!#उपग्रह की कुल ऊर्जा
View SolutionIf ‘$’ stands for addition, ‘@’ stands for subtraction, ‘#’ stands for multiplication and ‘&’ stands for division, then what is the value of यदि $? का अर्थ जोड़ है, ‘@’ का अर्थ घटाव है, ‘#’ का अर्थ गुना है और '&' का अर्थ विभाजन है, तो निम्नलिखित का मान क्या होगा ? 12 # 8 $ 36 & 3 @ 6?
View Solution
