विभिन्न त्रिज्याओं वाले साबुन के घोल के दो बुलबुले मिलकर एक हो जाते है । यदि नये बुलबुले में भरी वायु के आयतन में परिवर्तन V हो तथा कुल पृष्ठ - क्षेत्रफल में परिवर्तन S हो , तो दर्शाइए कि 3PV+4ST=0, जहाँ T साबुन के घोल का पृष्ठ - तनाव है ।
माना कि बुलबुलों की त्रिज्याएँ R1 वR2 तथा उन्हें मिलाने के बाद बने बड़े बुलबुले की त्रिज्या R है । प्रत्येक दशा में बुलबुलों के बाहर वायुमंडलीय दाब P है । यदि मिलाने से पहले बुलबुलों के भीतर दाब p1 व p2 तथा बाद में बड़े बुलबुले के भीतर दाब p हो , तब
p1=P+4TR1,p2=P+4TR2तथा p=P+4TR.
यदि बुलबुलों के संगत आयतन V1,V2 व V' हो , तब V1=43πR31,V2=43πR32तथा V'=43πR3.
यदि ताप नियत है , तब बॉयल के नियम से
p1V1+p2V2=pV'
अथवा (P+4TR1)(43πR31)+(P+4TR2)(43πR32)=(P+4TR)(43πR3)
अथवा P(43πR31+43πR32−43πR3)+4T3(4πR21+4πR22−4πR2)=0
पहले ब्रेकिट के भीतर की राशि बुलबुले के आयतन में परिवर्तन V है तथा दूसरे ब्रेकिट के भीतर की राशि पृष्ठ - क्षेत्रफल में परिवर्तन S है । अतः
PV+4T3S=0
अथवा 3PV+4ST=0.
यही दर्शाना था ।
Topper's Solved these Questions
- पृष्ठ - तनाव BOOK - NOOTAN HINDICHAPTER - पृष्ठ - तनाव EXERCISE - प्रश्नावली वस्तुनिष्ठ प्रश्न
23 Videos
- पृष्ठ - तनाव BOOK - NOOTAN HINDICHAPTER - पृष्ठ - तनाव EXERCISE - अतिलघु उत्तरीय
29 Videos
- द्रव्यमान-केन्द्र या संहति-केन्द्र BOOK - NOOTAN HINDICHAPTER - द्रव्यमान-केन्द्र या संहति-केन्द्र EXERCISE - प्रश्नावाली (EXERCISES) (वस्तुनिष्ठ प्रकार प्रश्न (OBJECTIVE TYPE QUESTIONS))
7 Videos
- प्रगामी आवर्त तरंगेंBOOK - NOOTAN HINDICHAPTER - प्रगामी आवर्त तरंगेंEXERCISE - वस्तुनिष्ठ प्रकार प्रशन
7 Videos
Similar Questions
द्रव का पृष्ठ - तनाव :
View Solutionकिस गुणधर्म के कारण द्रव का मुक्त पृष्ठ अपने क्षेत्रफल को न्यूनतम रखने का प्रयास करता है ?
View Solutionकिसी एकसमान ठोस शंकु के द्रव्यमान केन्द्र की उसके शीर्ष से दूरी z0 है। यदि शंक के आधार की त्रिज्या R तथा शंकु की ऊँचाई h हो तो z0 का मान निम्नांकित में से किसके बराबर होगा?
View Solutionनिम्नलिखित में से कोण-सी समीकरण सरल आवर्त प्रगामी तरंग को व्यक्त करती है ?
View SolutionSTP, पर 280 मिली CH4 और 140 मिली H2 के मिश्रण को पूर्णतया जलाया गया। यह मानते हुए कि सम्पूर्ण भाप , जल में संघनित हो जाती है , बनने वाले जल के भार तथा ऑक्सीजन के आवश्यक आयतन की गणना कीजिए ।
View Solutionयदि A और B किसी परीक्षण के प्रतिदर्श समष्टि S कि दो घटनाएँ हो , तो P(SA)=………
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionवृत के क्षेत्रफल में परिवर्तन कि दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए जबकि r = 3 सेमी. तथा r = 4 सेमी. है
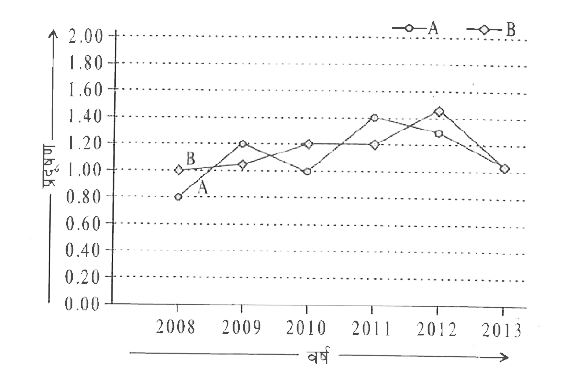
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
यदि B वर्ष 2010 तथा 2011 में कुल प्रदूषण 2.4 इकाई हो तो वर्ष 2008 व 2009 में प्रदूषण कितना मापा गया ?
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
यदि B वर्ष 2010 तथा 2011 में कुल प्रदूषण 2.4 इकाई हो तो वर्ष 2008 व 2009 में प्रदूषण कितना मापा गया ?

View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionदो अंको की एक संख्या में इकाई स्थान का अंक दहाई स्थान के अंक से 3 अधिक है यदि दोनों अंकों का जोड़ 11 हो तो संख्या निकालिए।
View Solutionदोहरान |प्रकाश संश्लेषण की प्रक्रिया में पौधे के विभिन्न भागों के कार्य |प्रकाश संश्लेषण के महत्वपूर्ण बिन्दु |यदि प्रकाश संश्लेषण नहीं हो तो क्या होगा?|प्रकाश संश्लेषण में भोजन किस रूप में बनता है |क्रियाकलाप |शैवाल में पोषण |सारांश
View Solutionक्या परिवर्तन करने के अन्य तरीके हो सकते है
View Solutionक्या परिवर्तन करने के अन्य तरीके भी हो सकते है
View Solution'जो अच्छे कुल में उतपन्न हुआ हो' इस शब्द समूह के लिए एक शब्द क्या है ?
View Solution
