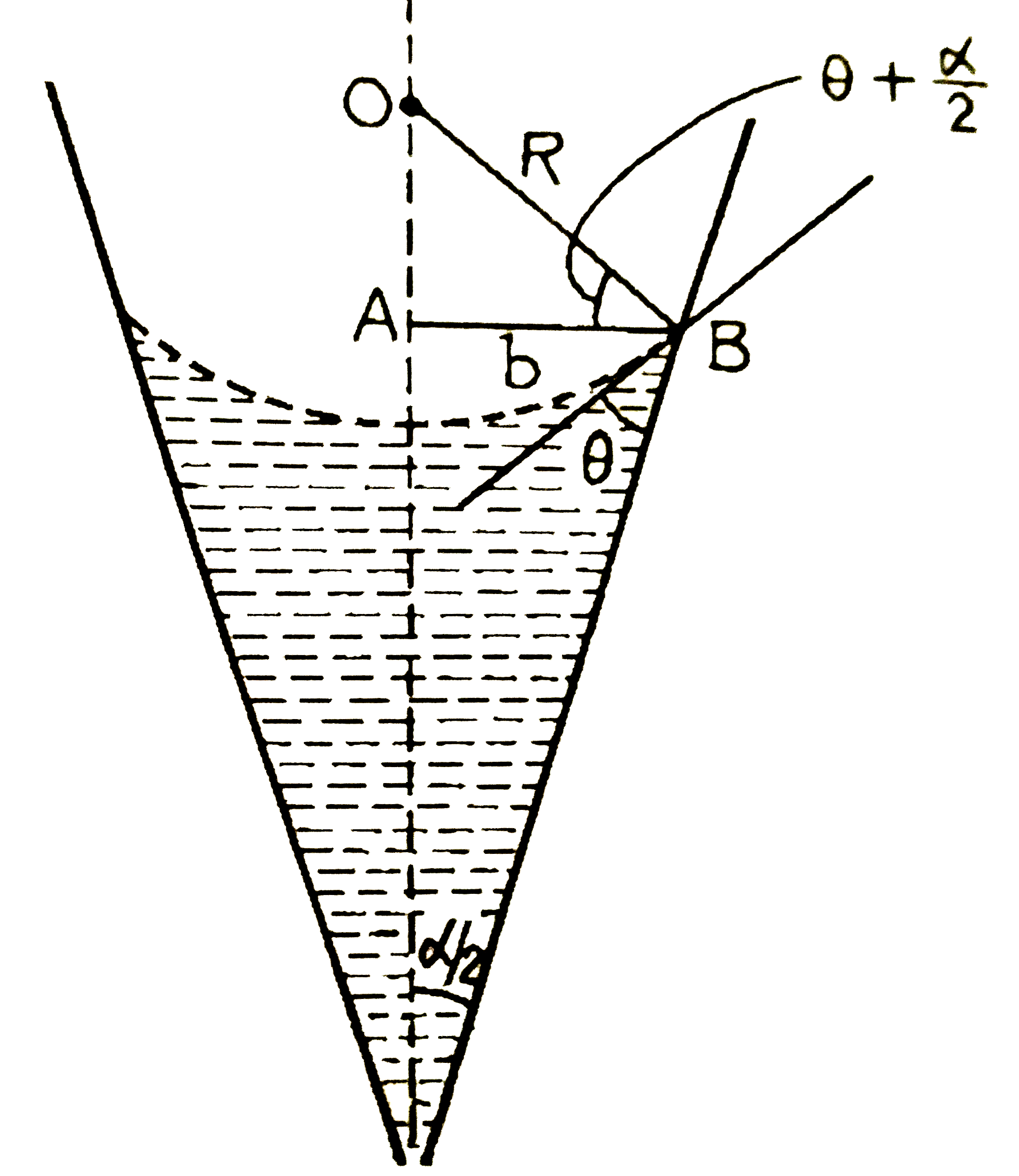
छिन्न शंकु ( truncated cone ) की आकृति वाली काँच की एक केशनली , जिसका शीर्ष कोणα है , के दो अंत सिरों के अनुप्रस्थ - काट की त्रिज्याएँ भिन्न है । केशनली को जल में ऊर्ध्वतः डुबाने पर केशनली में जल h ऊँचाई तक चढ़ जाता है , जहाँ इसकी अनुप्रस्थ - काट की त्रिज्या b है यदि जल का पृष्ठ - तनाव ( surface tension ) T , घनत्व ρ तथा काँच के साथ इसका स्पर्श कोण θ हो , तब h का मान है ( g गरुत्वीय त्वरण है ) :

2Tbρgcos(θ−α)
2Tbρgcos(θ+α)
2Tbρgcos(θ−α/2)
2Tbρgcos(θ+α/2)
The correct Answer is:D
यदि h ऊँचाई पर नवचन्द्रक ( meniscus ) की त्रिज्या R है । तब cos(θ+α2)=bR.
h ऊँचाई के जल स्तम्भ का दाब
p=2Tr
∴hρg=2TR
∴h=2TRρg
=2Tbρgcos(θ+α2).
Topper's Solved these Questions
- पृष्ठ - तनाव BOOK - NOOTAN HINDICHAPTER - पृष्ठ - तनाव EXERCISE - एनo सीo ईo आरo टीo प्रश्न
20 Videos
- पृष्ठ - तनाव BOOK - NOOTAN HINDICHAPTER - पृष्ठ - तनाव EXERCISE - अतिरिक्त प्रश्न
10 Videos
- पृष्ठ - तनाव BOOK - NOOTAN HINDICHAPTER - पृष्ठ - तनाव EXERCISE - आंकिक
36 Videos
- द्रव्यमान-केन्द्र या संहति-केन्द्र BOOK - NOOTAN HINDICHAPTER - द्रव्यमान-केन्द्र या संहति-केन्द्र EXERCISE - प्रश्नावाली (EXERCISES) (वस्तुनिष्ठ प्रकार प्रश्न (OBJECTIVE TYPE QUESTIONS))
7 Videos
- प्रगामी आवर्त तरंगेंBOOK - NOOTAN HINDICHAPTER - प्रगामी आवर्त तरंगेंEXERCISE - वस्तुनिष्ठ प्रकार प्रशन
7 Videos
Similar Questions
स्पष्ट कीजिए क्यों
(a) मस्तिष्क की अपेक्षा मानव का पैरो पर रक्त चाप अधिक होता है ।
(b) 6 km ऊँचाई पर वायुमंडलीय दाब समुद्र तल पर वायुमंडलीय दाब का लगभग आधा हो जाता है , यद्यपि वायुमंडल का विस्तार 100 km से भी अधिक ऊँचाई तक है ।
(c ) यद्यपि दाब , प्रति एकांक क्षेत्रफल पर लगने वाला बल होता है तथापि द्रव स्थैतिक दाब एक अदिश राशि है ।
View Solution1.0m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागो में बाँटा गया है । विभाजक दीवार में नीचे 20cm2 क्षेत्रफल का कब्जेदार दरवाजा है । टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है । दोनों भाग 4.0m ऊँचाई तक भरे गए है । दरवाजे को बंद रखने के आवश्यक बल परिकलित कीजिए ।
View Solutionदो सीधे 10 सेमी लम्बाई वाले समांतर तारों के बीच जो 05 सेमी दूर है , जल की के फिल्म बनाई जाती है , यदि तारों के बीच की दूरी 1 मिमी बढ़ायी जाये , तो कितना कार्य करना पड़ेगा ? जल का पृष्ठ - तनाव =0.072 न्यूटन /मीटर ।
View Solutionकिसी एकसमान ठोस शंकु के द्रव्यमान केन्द्र की उसके शीर्ष से दूरी z0 है। यदि शंक के आधार की त्रिज्या R तथा शंकु की ऊँचाई h हो तो z0 का मान निम्नांकित में से किसके बराबर होगा?
View Solutionनिम्नलिखित में से कोण-सी समीकरण सरल आवर्त प्रगामी तरंग को व्यक्त करती है ?
View Solutionसम्पर्क कोण #!#केशनली
View Solutionएक लाल ठोस जल में अविलेय है। हालांकि, जल में कुछ KI को मिलाने पर यह विलेय हो जाता है। एक परखनली में लाल ठोस को गर्म करने पर कुछ बैंगनी रंग के धूम मुक्त होते हैं और परखनली के ठंडे भागों पर एक धातु की बूंदें दिखाई देती हैं। लाल ठोस है -
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionजल में क्षारीय मृदा धातुओं के सल्फेट की विलेयता वर्ग में नीचे जाने पर घटती है क्योंकि:
View Solutionजब एक आयोडाइड लवण में क्लोरीन जल के आधिक्य को मिलाया जाता है तो आयोडीन की ऑक्सीकरण अवस्था में निम्न परिवर्तन होता है:
View Solution277 K पर जल के वियोजन की मात्रा 1xx10^(-7)% है जल के आयनिक गुणनफल का मान है
View Solutionजब एक फ्लोराइड को काँच की नली में सांद्र H_(2)SO_(4) के साथ गर्म किया जाता है और यदि जल की एक बूंद को कांच की नली के मुख पर रखा जाता है, तो निम्नलिखित में से किसका श्वेत निक्षेप निर्मित होता है:
View SolutionCIF_4^(+) में केंद्रीय रूप के चारों ओर की आकृति है:
View Solutionनिम्नलिखित यौगिक के जल अपघटित उत्पादों में से एक, काँच पात्र की सिलिका के साथ अभिक्रिया नहीं करता है?
View Solutionनिम्नलिखित में से किस लवण के जल-अपघटन की मात्रा लवण के विलयन की सांद्रता पर निर्भर नहीं करती है?
View Solutionएक साइक्लोहेक्सेनोन, अम्ल उत्प्रेरक मात्रा की उपस्थिति में डाइमेथिलएमीन के साथ अभिक्रिया पर एक यौगिक का निर्माण करता है, यदि अभिक्रिया के दौरान जल का लगातार निष्कासन किया जाता है, तब निर्मित यौगिक को सामान्यतः जाना जाता है
View Solution
