एक एकसमान बेलन जिसकी लम्बाई L , द्रव्यमान M तथा परिच्छेद क्षेत्रफल A है एक द्रव्यमानहीन स्प्रिंग द्वारा एक स्थिर बिंदु से ऊर्ध्वाधर लटका है यह संतुलन स्थिति में घनत्व p के द्रव में आधा डूबा है जब बेलन को थोड़ा नीचे खींच कर छोड़ दिए जाता है तो वह छोटे आयाम के साथ ऊर्ध्वाधर दोलन करने लगता है यदि स्प्रिंग का बल-नियतांक k हो , तो बेलन की आवृति है
12π(k−ApgM)12
12π(k+ApgM)12
12π(k+pgL2M)12
12π(k+ApgApg)12
The correct Answer is:B
लम्बाई L का बेलन घनत्व p के द्रव में आधा डूबा है अतः बेलन पर उत्क्षेप बल =A(L/2)pg . यदि बेलन कि संतुलन स्थिति में स्प्रिंग में विस्तार l हो तब
klMg−A(L/2)pg (i)
जब बेलन को अल्प दूरी y ( माना ) से नीचे को विस्थापित किया जाता है , तब स्प्रिंग में उत्पन्न प्रत्यास्थ प्र्त्यानं बल k(l+y) ही तथा बेलन पर परिणामी बल
F=−k(l+y)+[Mg−A(L2+y)pg]
समीकरण (i) प्रयुक्त करने पर
F=−Mg+A(L/2)pg−ky+Mg−A(L2+y)pg
=−(K+Apg)y
बेलन में उत्पन्न त्वरण
α=FM=−(k+ApgM)y=−ω2y
जहाँ ω=√k+ApgM स्पष्ट है कि बेलन की गति सरल आवर्त है जिसकी आवृत्ति है :
n=ω2π=12π√k+ApgM
Topper's Solved these Questions
- सरल आवर्त गति BOOK - NOOTAN HINDICHAPTER - सरल आवर्त गति EXERCISE - आंकिक
45 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
- सार्वत्रिक गुरुत्वाकर्षण BOOK - NOOTAN HINDICHAPTER - सार्वत्रिक गुरुत्वाकर्षण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए
15 Videos
Similar Questions
सरल आवर्त गति करते हुए एक कण का विस्थापन-समय सम्बन्ध समीकरण y=0.50sin(500rt+0.5) द्वारा प्रदर्शित है, जहाँ दूरी सेमी में तथा समय सेकण्ड में है। कण का आयाम, कोणीय आवृत्ति, आवृत्ति तथा प्रारम्भिक कला ज्ञात कीजिये ।
View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View Solutionसूर्य के चारो ओर दीर्घवृत्तीय कक्षा में गतिमान ग्रह की स्थितियों A, B तथा C पर गतिज ऊर्जाएं क्रमश: KA,KB और KCहै। AC दीर्घ अक्ष है तथा सूर्य की स्थिति S पर SB चित्रानुसार दीर्घ अक्ष AC पर लम्ब है। तब :
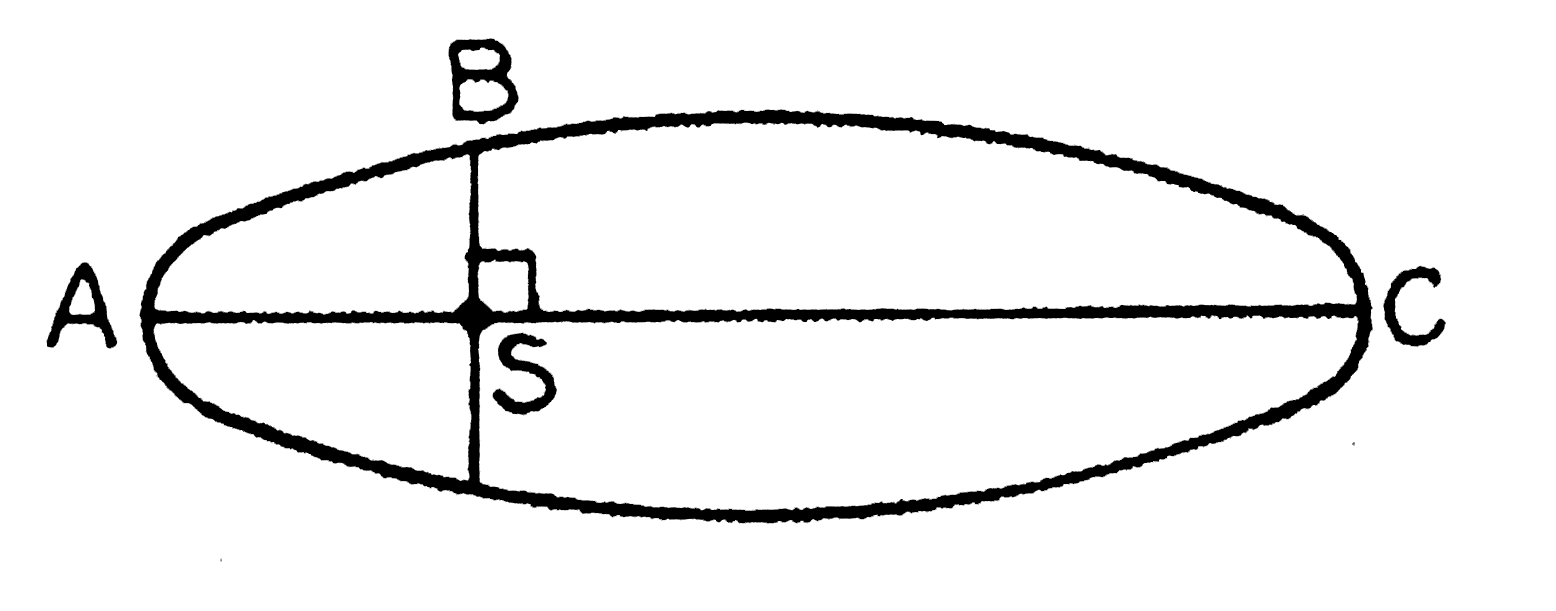
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionताश के 52 पत्तो की एक सुनिश्चित गड्डी में से एक पत्ता यदृच्छया निकाला जाता है | यदि
E : निकाला गया पत्ता हुकुम का है |
F : निकाला गया पत्ता इक्का है , तो E तथा F घटनाएँ है -
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View SolutionA cylinder of radius 4.5 cm and height 12 cm just fits in another cylinder completely with their axis perpendicular. What is the radius (in cm) of second cylinder? एक बेलन जिसकी त्रिज्या 4.5 से.मी. तथा ऊँचाई 12 से.मी. है, को एक अन्य बेलन में उनके अक्षों के लम्बवत् पूरी तरह से सम्माहित किया गया है। दूसरे बेलन की त्रिज्या (से.मी. में) क्या है?
View SolutionA ribbon of equal width and length l is wrapped around the curved surface of a right circular cylinder to cover it completely. If the base circumference of this cylinder is c, then how many times the ribbon was wrapped around the cylinder ?
एक समान चौड़ाई वाले किसी रिबन, जिसकी लम्बाई 1 है, को एक लम्ब वृत्तीय बेलन (सिलिंडर) के वक्र पृष्ठ (कवर्ड सरफेस ) पर पूर्ण रूप से कवर करने के लिए लपेटा जाता है |यदि बेलन (सिलिंडर) के आधार की परिधि c है, तो बेलन (सिलिंडर ) पर रिबन से कितनी बार लपेटा गया :
View Solutionधातु आयन का एक विलयन जब KI के साथ उपचारित किया जाता है, तो यह एक लाल अवक्षेप देता है जो KI के आधिक्य में विलेय होकर एक रंगहीन विलयन देता है। इसके अलावा, धातु आयन का विलयन, कोबाल्ट (II) थायोसायनेट के विलयन के साथ उपचारित करने पर एक गहरा नीला क्रिस्टलीय अवक्षेप देता है। धातु आयन है
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solution
