एक समबाहु त्रिभुज में, सिद्ध कीजिए कि केन्द्रक और परिवृत्त का केन्द्र (परिकेन्द्र) सम्पाती होते हैं |
दिया है : एक समबाहु त्रिभुज, ABC जिसमें D, E और F क्रमश : BC, CA और AB के मध्य बिन्दु हैं |
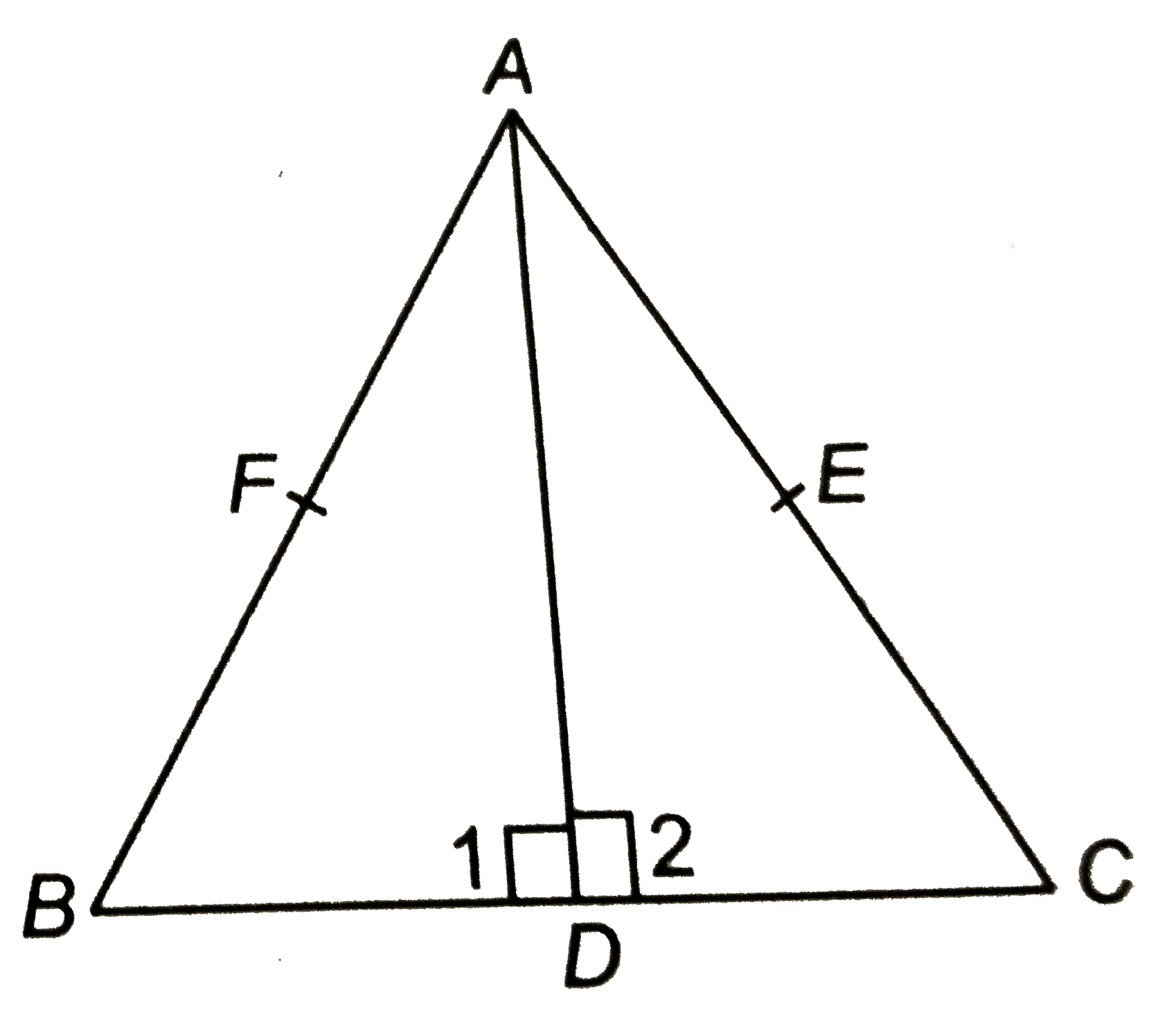
सिद्ध करना है : केन्द्रक और परिकेन्द्र सम्पाती हैं |
रचना : माध्यिका AD खींचते हैं |
उपपत्ति :
परन्तु
और
का लम्ब समद्विभाजक है |
इसका अर्थ है कि समबाहु त्रिभुज की माध्यिका और लम्ब समद्विभाजक समान हैं |
माध्यिकाओं का प्रतिच्छेद बिन्दु = लम्ब समद्विभाजकों का प्रतिच्छेद बिन्दु
केन्द्रक = परिकेन्द्र
अर्थात एक समबाहु त्रिभुज के केन्द्रक और परिकेन्द्र हैं |
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10A21videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10B19videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन5videos
रेखाएं और कोण
- BOOK - NOOTAN HINDICHAPTER - संख्या पद्धतिEXERCISE - विविध प्रश्नावली (लघु उत्तरीय प्रश्न)10videos
संख्या पद्धति
Similar Questions
एक वृत्त में 10 सेमी लम्बी जीवा केन्द्र से 12 सेमी कि दूरी पर है | इसी वृत्त के केन्द्र से 5 सेमी की दूरी पर स्थित जीवा की लम्बाई क्या होगी ?
03:54View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि ∠ACB=25∘, तो ∠AOB ज्ञात कीजिए |
 06:12View Solution
06:12View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC04:36View Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
03:33View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
05:57View Solutionदिखाइए कि किसी त्रिभुज में भुजाओं के लम्ब अर्धक संगामी होते हैं |
05:13View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
06:40View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
04:32View Solutionउस त्रिभुज के परिकेन्द्र और परिवृत्त की त्रिज्या ज्ञात कीजिए जिसके शीर्ष क्रमश :(4,6),(0,4) और (6,2) है ।
06:21View Solutionबिंदुओं (0,0),(0,8) और (4,6) से बने त्रिभुज का केन्द्रक और परिकेन्द्र ज्ञात कीजिए ।
03:33View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
34:41View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
26:36View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
02:36View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)01:11View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
01:11View Solutionज्या का नियम और कोज्या का नियम क्या होते हैं?
43:44View Solution

