सिद्ध कीजिए कि चक्रीय समान्तर चतुर्भुज आयत होता है |
दिया है : एक वृत्त के अन्दर समान्तर चतुर्भुज ABCD
सिद्ध करना है : ABCD एक आयत है |
उपपत्ति : ABCD एक समान्तर चतुर्भुज है |
∴ ∠A=∠C …(1)
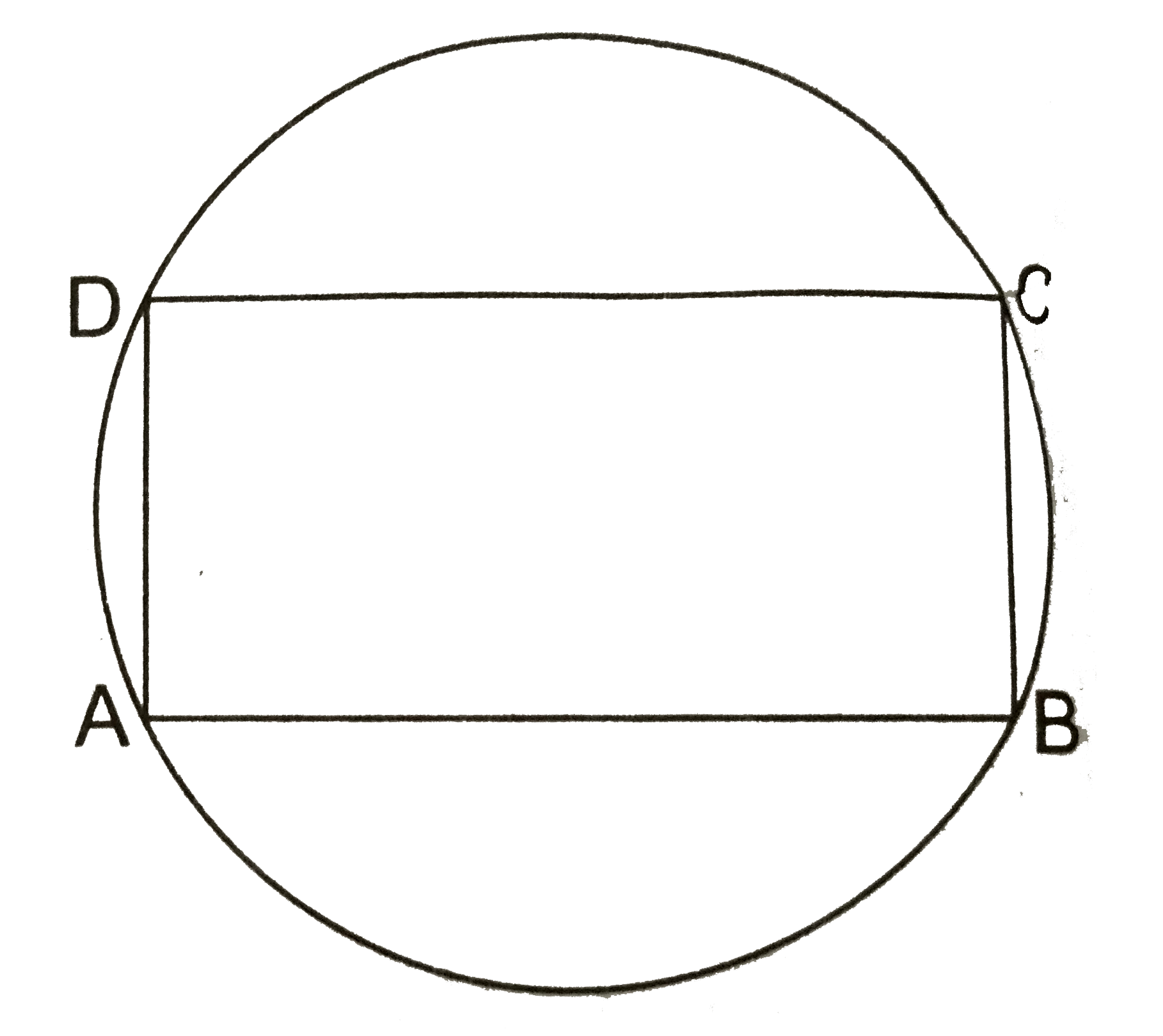
ABCD एक चक्रीय चतुर्भुज है |
∴ ∠A+∠C=180∘
⇒ ∠A+∠A=180∘
⇒ 2∠A=180∘
⇒ ∠A=90∘
∴ समान्तर चतुर्भुज का एक कोण समकोण है |
⇒ ABCD एक आयत है |
Topper's Solved these Questions
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.6 ऐच्छिक)
10 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - विविध प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
10 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 10.4)
6 Videos
- रेखाएं और कोण BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन
5 Videos
- संख्या पद्धतिBOOK - NOOTAN HINDICHAPTER - संख्या पद्धतिEXERCISE - विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
10 Videos
Similar Questions
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों की केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण अंतरित करती है |
View Solutionयदि r त्रिज्या के वृत्त का केन्द्र O है तथा O से r/2 दुरी पर जीवा AB है तो ∠BAO ज्ञात कीजिए |
View Solution5 सेमि और 3 सेमि त्रिज्या वाले दो वृत्त, दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सेमी है | उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए |
View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionयदि p मूलबिंदु से रेखा xa+yb=1 पर लम्ब कि लम्बाई है तथा a2,p2,b2 समान्तर श्रेढी में है , तब सिद्ध कीजिए कि a4+b4=0
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय संख्याएँ है-
32√5
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=[→a.→d][→a→b→c]
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=(→a.→d)[→a→b→c]
View Solution