दीर्घवृत्त x2a2+y2b2=1 का क्षेत्रफल ज्ञात कीजिये |
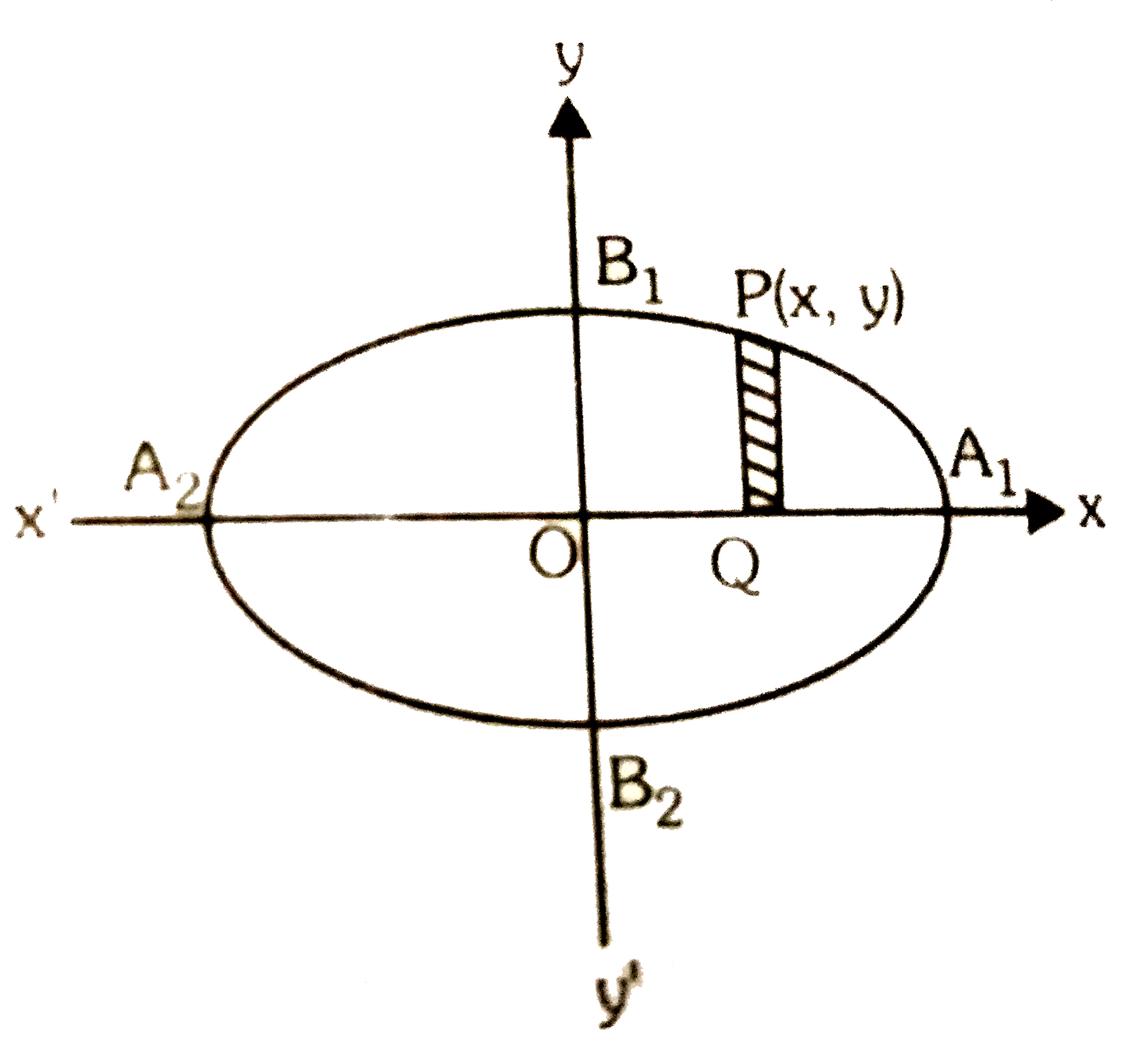
माना दीर्घवृत्त x - अक्ष तथा y - अक्ष को क्रमशः A1,A2 और B1,B2 पर काटता है | वक्र दोनों अक्षो के परितः सममित है | अतः इसके एक चतुर्थांश का क्षेत्रफल ज्ञात करके उसे चार से गुणा करने पर दीर्घवृत्त का क्षेत्रफल ज्ञात हो जाएगा |
माना वक्र पर स्थित बिंदु P(x,y) पर हमने एक प्रारम्भिक पट्टी PQ ली जिसकी लम्बाई y तथा चौड़ाई δx है | अतः प्रारम्भिक पट्टी का क्षेत्रफल = y⋅δx | हम पुरे चतुर्थांश को इसी प्रकार की प्रारम्भिक पट्टियों में विभाजित करके उनके क्षेत्रफलों का योग करें तब हमे वक्र के प्रथम चतुर्थांश में स्थित क्षेत्र का क्षेत्रफल प्राप्त होगा जिसे चार से गुणा करने पर पुरे दीर्घवृत्त का क्षेत्रफल ज्ञात हो जाएगा | स्पष्ट है कि समाकलन सीमायें '0 से a' होंगी | अतः
∵x2a2+y2b2=1
⇒y2b2=1−x2a2
⇒y=ba√a2−x2
अतः A=4∫a0ydx=4ba∫a0√(a2−x2)dx
माना x=asinθ⇒dx=acosθ/dθ
तथा √a2−x2=acosθ
सीमायें x=0 पर θ=0 तथा x=a पर θ=π/2
अतः नयी समाकलन सीमायें '0 से π/2 ' होंगी|
∴A=4ba⋅a2∫π/20cos2θdθ
=2ab∫π/20(1+cos2θ)dθ
=2ab[θ+sin2θ2]π/20
=2ab[(π/2+sinπ2)−(0+sin02]
=πab वर्ग इकाई
Topper's Solved these Questions
- समाकलन के सरल अनुप्रयोग BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन के सरल अनुप्रयोग EXERCISE - अभ्यास प्रश्न 17.1
12 Videos
- समाकलन के सरल अनुप्रयोग BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन के सरल अनुप्रयोग EXERCISE - अभ्यास प्रश्न 17.2
9 Videos
- समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
24 Videos
- समाकलन क्रमशः BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन क्रमशः EXERCISE - स्वमूल्यांकन परीक्षण
20 Videos
Similar Questions
y=ex,x=0 से x=a तक
View Solutionपरवलय y2=4ax तथा रेखा y=2x द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
View Solutionमान ज्ञात कीजिए -∫(4e3x+1)dx
View Solution1x2−9
View Solutionवक्र y=logx,x−अक्ष,x=1/2तथाx=3/2 से घिरे भाग का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्रो y=√5−x2तथा y = | x - 1 | से सीमाबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
View Solutionदीर्घवृत्त x2a2+y2b2=1 की किसी स्पर्शी तथा अक्षो से बने त्रिभुज का न्यूनतम क्षेत्रफल होगा :
View Solutionपरवलय y=4−x2 तथा x -अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionदीर्घवृत्त x24+y29=1 से घिरे क्षेत्र का क्षेत्रफल 6π2 वर्ग मात्रक है।
View Solutionरेखा x+y+z+1=0,4x+y−2z+2=0 का सममित रूप ज्ञात कीजिये।
View Solutionवृत्त x2+y2=a2 तथा वक्र y=|x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionप्रथम चतुर्थांश में रेखाओं x = a, y = a तथा x2+y2=a2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्र y=2√x तथा x=0,x=1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutiony = |x|, x= - 3, x = 1 व x-अक्ष से परिबध्द क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्रों y2=2x तथा x2+y2=8 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवृत्त x2+y2=16 तथा परवलय x2=6y से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solution