Doubtnut Promotions Sticky

समाकलन के प्रयोग से क्षेत्र
{(x,y):x2+y2≤2ax,y2>ax,x,y≥0}
का क्षेत्रफल ज्ञात कीजिये |

Text Solution
Verified by Experts

दिया गया क्षेत्र -
{(x,y):x2+y2≤2ax,y2>ax,x,y≥0}
अब x2+y2≤2ax
⇒x2+y2−2ax≤0
⇒x2−2ax+a2+y2≤a2
⇒(x−a)2+y2≤a2
यह केंद्र (a,0) तथा त्रिज्या a के वृत्त की समीकरण को निरूपित करता है |
y2≥ax
यह शीर्ष (vertex ) (0 , 0 ) तथा अक्ष x - अक्ष के परवलय की समीकरण को निरूपित करता है |
अब, गोले (x−a)2+y2=a2 तथा परवलय y2=ax का प्रतिच्छेदन बिंदु है -
(x−a)2+ax=a2
⇒x2+a2−2ax+ax=a2
⇒x2−ax=0
⇒x(x−a)=0
⇒x=0,a
जब, x =0 , y2=0⇒y=0
जब, x = a, y2=a2⇒y=±a
अतः प्रतिच्छेदन बिंदु O(0,0),A(a,a) तथा B(a,−a) है | दिए गए वक्र (curve ) का आलेख निम्न है -
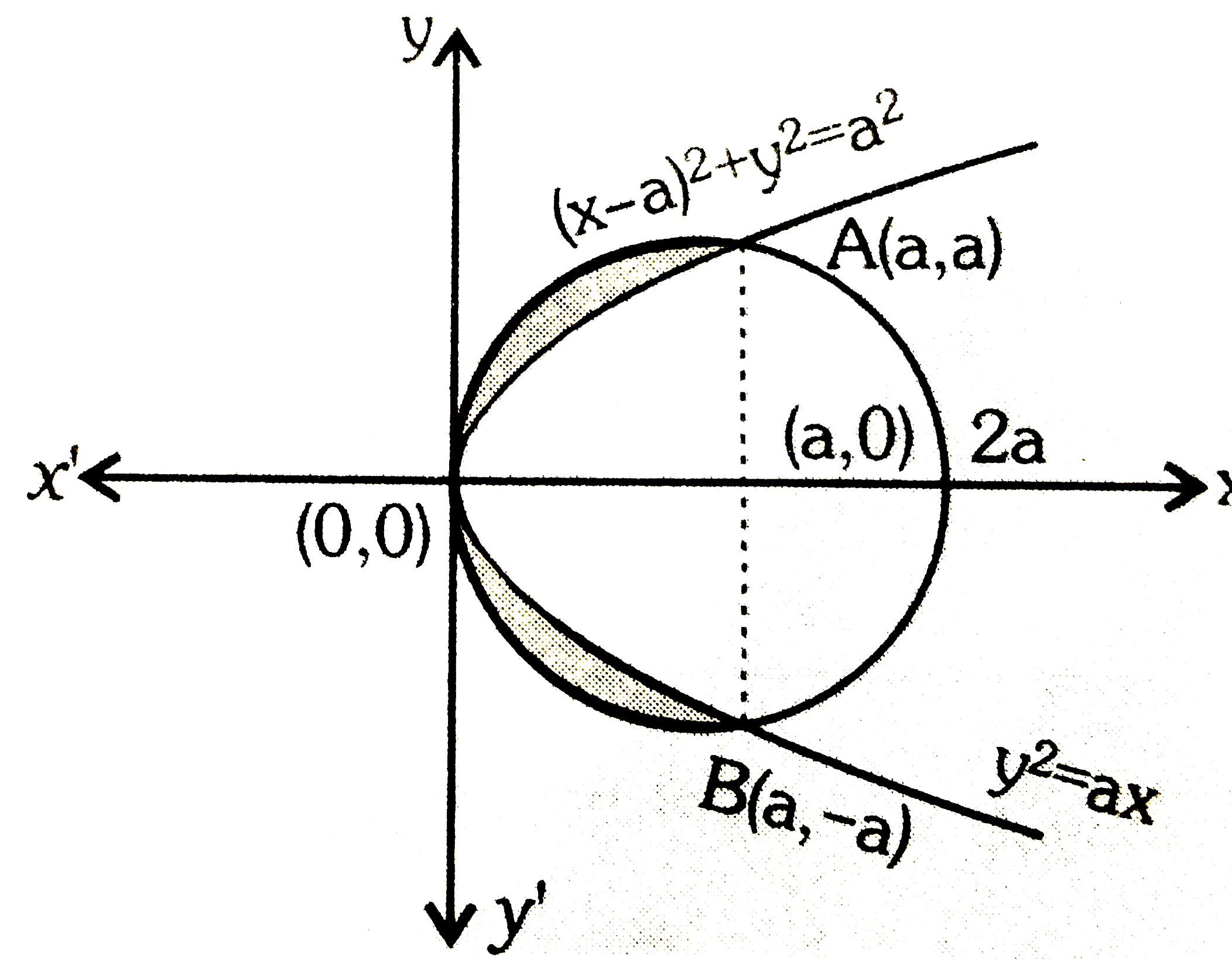
ocr_image
अभीष्ट क्षेत्रफल -
=∫a0y (वृत्त ) dx - ∫a0y ( परवलय ) dx
=∫a0√a2−(x−a)2dx−∫a0√axdx
=[x−a2√a2−(x−a)2+a22sin−1(x−aa)]−0a−[√ax3/23/2]a0
=[0+a22sin−1(0)−{0+a22sin−1(1)}]−23√a[a3/2−0]
=[0−{−a22×π2}]−23a2[∵sin−1(−θ)=−sin−1θ]
=a2π4−23a2=a2[π4−23] वर्ग इकाई

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12MATHSINTEGRALS

Topper's Solved these Questions

Similar Questions