यदि →a तथा →b दो सदिश है, तो सिद्ध कीजिये कि
(i) ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣ (ii) ∣∣→a−→b∣∣≥|→a|−∣∣→b∣∣
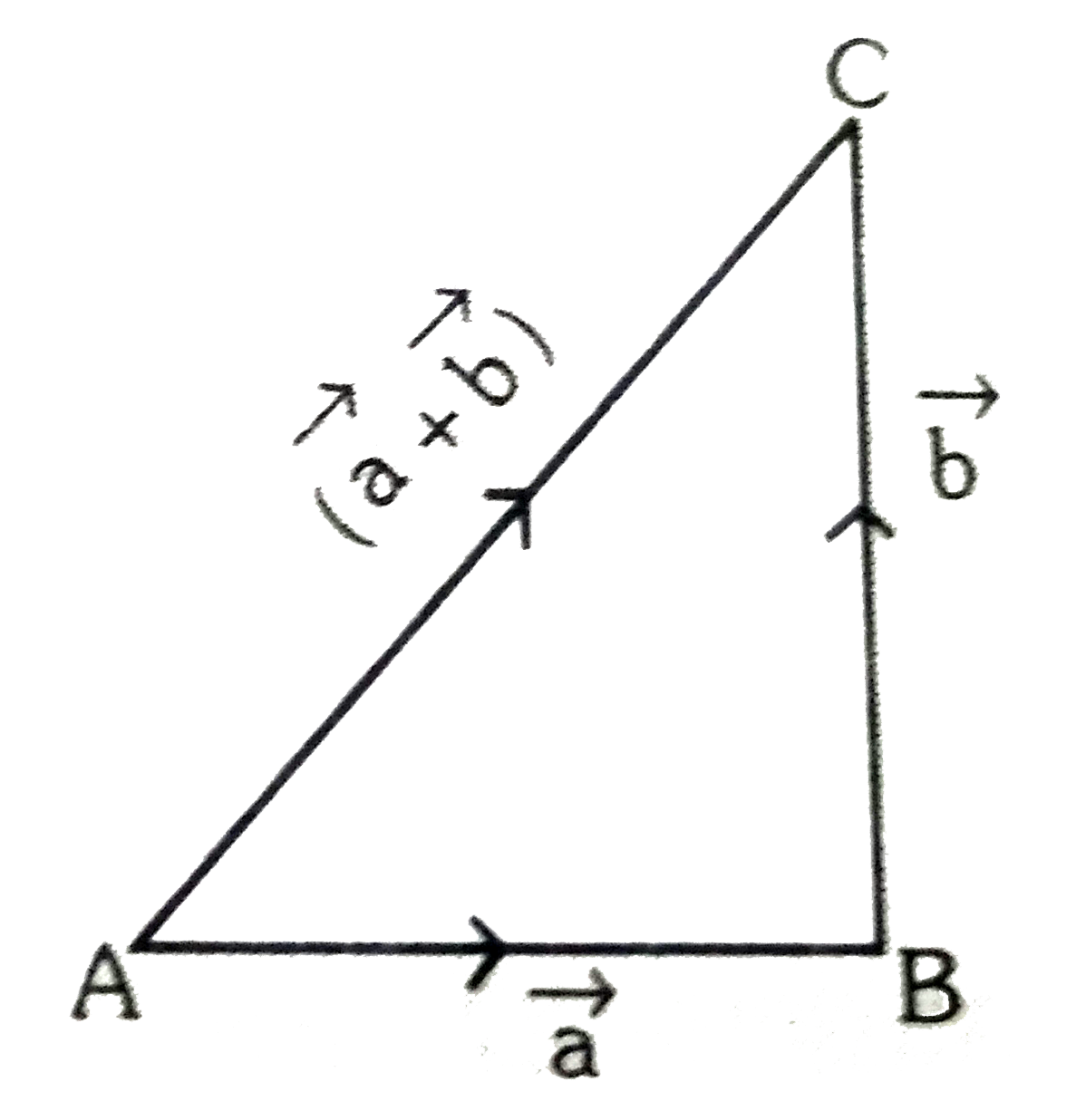
(i) माना −−→AB=→a,−−→BC=→b
∴−−→AC=−−→AB+−−→BC
=→a+→b
हम जानते है कि Δ की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
∴−−→AB+−−→BC>−−→AC
या |→a|+∣∣→b∣∣>∣∣→a+→b∣∣
∣∣→a+→b∣∣<|→a|+∣∣→b∣∣ ...(1)
यदि बिन्दु A, B, C सरेख है, तब

−−→AB=→a,−−→BC=→b
−−→AC=−−→AB+−−→BC
⇒∣∣∣−−→AC∣∣∣=∣∣∣−−→AB∣∣∣+∣∣∣−−→BC∣∣∣
∣∣→a+→b∣∣=|→a|+∣∣→b∣∣ ...(2)
∴ समीकरण (1) व (2) से
∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
(ii) |→a|=∣∣→a−→b+→b∣∣≤∣∣→a−→b∣∣+∣∣→b∣∣
|→a|−∣∣→b∣∣≤∣∣→a−→b∣∣
या ∣∣→a−→b∣∣≥|→a|−∣∣→b∣∣

Topper's Solved these Questions
- सदिश बीजगणित BOOK - BALAJI PUBLICATIONCHAPTER - सदिश बीजगणित EXERCISE - अभ्यास प्रश्न 19.1
12 Videos
- सदिश बीजगणित BOOK - BALAJI PUBLICATIONCHAPTER - सदिश बीजगणित EXERCISE - अभ्यास प्रश्न 19.2
19 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
- सदिश राशियों का गुणनफल BOOK - BALAJI PUBLICATIONCHAPTER - सदिश राशियों का गुणनफल EXERCISE - बहुविकल्पीय उत्तरीय प्रश्न
25 Videos
Similar Questions
ABCD एक चतुर्भुज है, तो सिद्ध कीजिये की −−→BA+−−→BC+−−→CD+−−→DA=2−−→BA
View Solutionएक आयत ABCD की दो आसन्न भुजाओं AB तथा BC की लम्बाईयाँ क्रमशः 8 तथा 6 मीटर है। बिन्दु A पर रखे एक पिण्ड पर AB, AC तथा AD के अनुदिश क्रमशः 3,5,4 न्यूटन के बल लगे है। परिणामी बल का परिमाण तथा दिशा ज्ञात करो।
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View Solutionयदि सदिश 2ˆi+ˆj+ˆk तथाˆi−ˆj+λ लम्बवत है , तब λ=
View SolutionIf →a,→b are two vectors, then write the truth value of the following statements: →a=−→b|→a|=∣∣→b∣∣ |→a|=∣∣→b∣∣→a=±→b |→a|=∣∣→b∣∣→a=→b
View Solutionif | vec a | = | vec b | then find [(vec a + vec b) * (vec a-vec b)]
View SolutionIf |vec(a)+vec(b)|ge|vec(a)-vec(b)| then angle between vec(a) and vec(b) may be
View SolutionEstablish the following vector in equalities:
(i) ∣∣→a−→b∣∣≤|→a|+∣∣→b∣∣
(ii) ∣∣→a−→b∣∣≥|→a|−∣∣→b∣∣
What does the equality sign apply ?
View Solutionकिस दशा में (i) →A+→B=→A−→B
(ii) ∣∣→A+→B∣∣=∣∣→A−→B∣∣
View Solutionयदि →a,→b,→c मात्रक सदिश इस प्रकार हैं कि →a+→b+→c=0तो→a⋅→b+→b⋅→c+→c⋅→a का मान ज्ञात कीजिए ।
View Solutionयदि →A=→i+→j+→k,→C=→j−→k तो →B निकाले ताकि →A×→B=→C और →A.→B=3.
View SolutionObserve the following list
List-IList-IIA.[→a→b→c]1.|→a|∣∣→b∣∣cos(→a.→b)B.(→c×→a)×→b2.(→a.→c)→b−(→a.→b)→cC.→a×(→b×→c)3.→a.→b×→cD.→a.→b4.|→a|∣∣→b∣∣5.(→b−→c)→a−(→a.→b)→c
Then the correct match for List-I from list II is
View Solutionयदि →a,→b,→c समतलीय हो , तो [→a→b→c]=………. होगा।
View Solutionसदिश →a,→b तथा →a×(→b×→a)………… है।
View SolutionFor the vectors →a and →b show that
(i) ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣ (ii) ∣∣|→a|−∣∣→b∣∣∣∣≤∣∣→a−→b∣∣
View Solution
