यदि समकोणीय षष्टफलक की कोर a,b,c है, तो सिद्ध कीजिए की षष्टफलक के विकर्णों के बीच का कोण cos−1(±a2±b2±c2a2+b2c2) है।
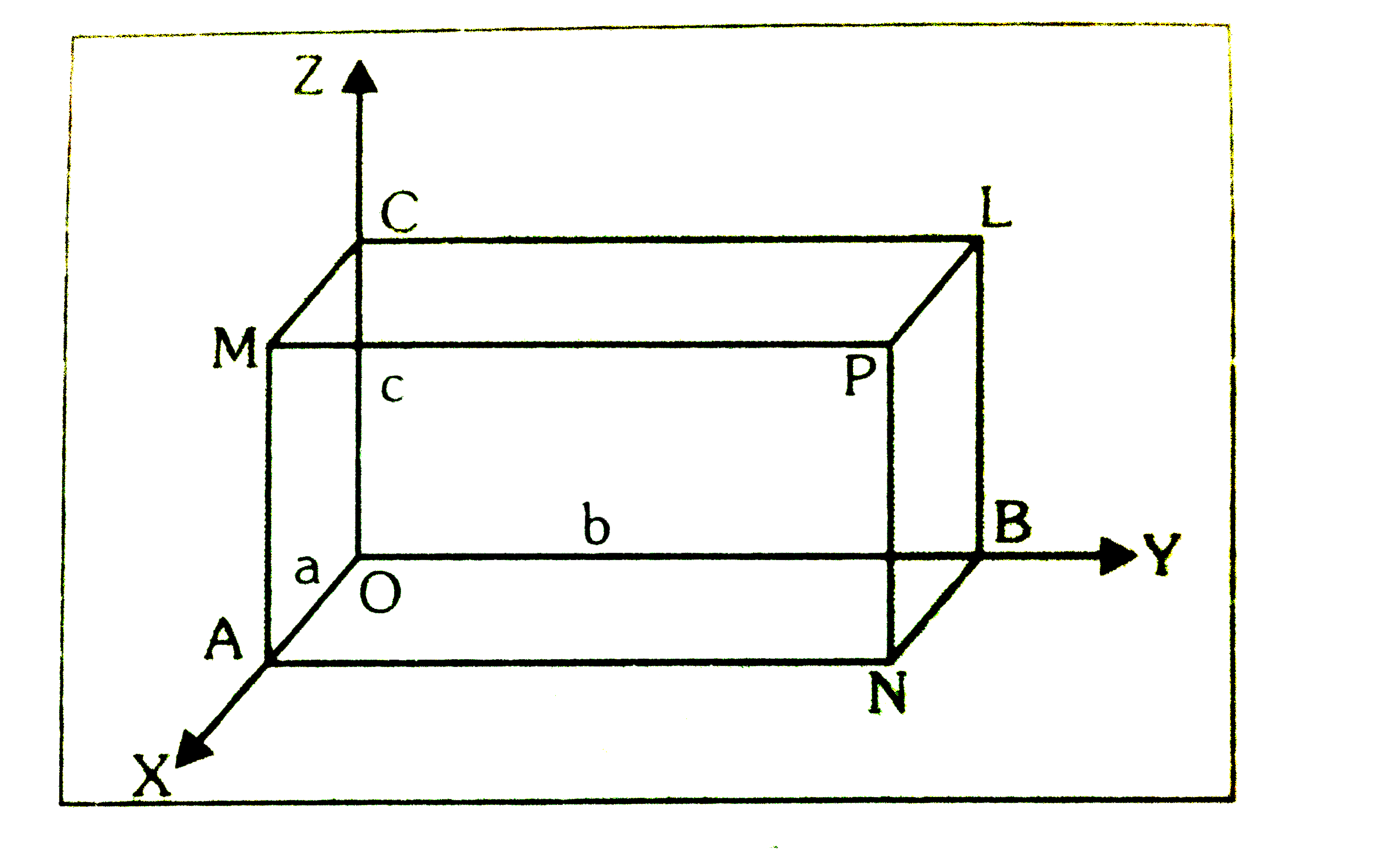
निम्न चित्र के अनुसार OA=a,OB=b तथा OC=c इसलिए शीर्षो के निर्देशांक निम्न है।
O(0,0,0),A(a,0,0),B(0,b,0),
C(0,0,c),P(a,b,c),L(0,b,c)
M(a,0,c) तथा N(a,b,0)
विकर्ण OP,AL,BM तथा CN के दिक् अनुपात क्रमशः (a,b,c),(−a,b,c),(a,−b,c) तथा (a,b−c) है।
विकर्ण OP,AL,BM तथा CN की दिक् कोज्याएं
(a√a2+b2+c2,b√a2+b2+c2,c√a2+b2+c2)
(a√a2+b2+c2,b√a2+b2+c2,c√a2+b2+c2)
(a√a2+b2+c2,−b√a2+b2+c2,c√a2+b2+c2)
(a√a2+b2+c2,b√a2+b2+c2,−c√a2+b2+c2)
माना OP अतः AL, के बीच का कोण θ1 है तो
cosθ1==(−a2+b2+c2)(a2+b2+c2)
⇒θ1=cos−1(−a2+b2+c2a2+b2+cc)
अब माना θ2OP तथा BM, के बिक का कोण है तब
θ1=cos−1(a2−b2+c2a2+b2+cc)
इसी पक्रार अन्य विकणों के बीच का कोण भी हम प्राप्त कर सकते है।
इसलिए षष्टफलक के विकर्णों के बीच का कोण cos−1(±a2±b2±c2a2+b2+cc) होगा ।
Topper's Solved these Questions
- त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल EXERCISE - अभ्यास प्रश्न 22.1
16 Videos
- त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल EXERCISE - अभ्यास प्रश्न 22.2
21 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
- द्विआधारी संक्रियाएँ BOOK - BALAJI PUBLICATIONCHAPTER - द्विआधारी संक्रियाएँ EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
Similar Questions
निम्नलिखित सदिशों की दिक् कोज्याये ज्ञात कीजिए-
(i) 2ˆi+2ˆj−ˆk
(ii)6ˆi−2ˆj−3ˆk
View Solutionउस रेखा का समीकाण ज्ञात कीजिए जो बिन्दु (1,2,3) से होकर जाती है तथा रेखा −x−21=y+37=2z−63 के समान्तर है ।
View Solutionx sin x का समाकलन कीजिए-
View Solutionसिद्ध कीजिए की a∗b=a+2b द्वारा प्रदर्शित ⋅:R×R→R क्रमविनिमेय नहीं है|
View SolutionIf the edges of a rectangular parallelepiped are a,b, c, prove that the angles between the four diagonals are given by cos−1(±a2±b2±c2a2+b2+c2).
View Solutionयदि A , B और C त्रिभुज ABC के अंतः कोण हों, तो दिखाइए कि
sin(B+C2)=cos(A2)
View Solutionत्रिभुज ABC में कोण C समकोण है । यदि बिंदु A और B निर्देशांक क्रमशः (−3,4) और (3,−4)हो , तो सिद्ध कीजिये की ΔABC के परिवृत्त का समीकरण x2+y2=25 होगा ।
View Solutionयदि ¯a+¯b+¯c=¯0 तथा सदिशों ¯b और ¯c के बीच का कोण θ हो, तो सिद्ध कीजिए कि
cosθ=|¯a|2−∣∣¯b∣∣2−|¯c|22∣∣¯b∣∣|¯c|.
View Solutionसिद्ध कीजिए की (1−4x)1/2 के प्रसार में xr का गुणांक
⌊2r⌊r⌊r है|
View Solutionयदि a, b, c समान्तर श्रेढ़ी में हो, तो सिद्ध कीजिए की
a2(b+c)+b2(c+a)+c2(a+b)=29(a+b+c)3.
View Solutionसिद्ध कीजिए की रेखाओं xa+yb=1 और xa−yb=1 के बीच का कोण 2tan−1ba है।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि अतिपरवलय x2a2−y2b2=1 की उत्केन्द्रता e तथा अन्तःस्पर्शियों के बीच का कोण α हो, तो secα2=
View Solutionरेखा x−2a=y−2b=z−2c तथा समतल ax+by+cz+6=0 के बीच का कोण है -
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solution
