दर्शाइए कि n, n + 2 या n + 4 में से केवल एक ही 3 से विभाजित होता है । यहाँ n एक पूर्णांक है ।
हम जानते हैं की कोई भी धनात्मक पूर्णांक 3q, 3q + 1 या 3q + 2 के रूप का होता है । (q एक पूर्णांक है) इनमे से केवल एक ही स्थिति होगी ।
स्थिति I. यदि n = 3q तब यह 3 से विभाजित है ।
अब n=3q ⇒ n+2=3q+2
⇒ n+2 को 3 से विभाजित करने पर शेषफल 2 प्राप्त होता है । अत: n + 2, 3 से विभाजित नहीं है ।
तथा n=3q ⇒ n+4=3q+4=3(q+1)+1
⇒ (n+4) को 3 से विभाजित करने पर शेषफल 1 प्राप्त होता है, अत: से विभाजित नहीं है अत: n + 4, 3 से विभाजित नहीं है, इस स्थिति में n, 3 से विभाजित है परन्तु n + 2 तथा n + 4 नहीं ।
स्थिति II. यदि n = 3q + 1
∵n=3q+1 को 3 से विभाजित करने पर शेषफल 1 प्राप्त होता है । अत: n, 3 से विभाजित नहीं है ।
अब n=3q+1 ⇒ n+2=3q+1+2=3(q+1) ⇒ n+2,3 से विभाजित है |
तथा n=3q+1 ⇒n+4=(3q+1)+4=3q+5=3(q+1)+2
⇒(n+4) को 3 से विभाजित करने पर शेषफल 2 प्राप्त होता है । अत: (n + 4), 3 से विभाजित नहीं है अत: (n + 2), 3 से विभाजित है, परन्तु n तथा (n + 4) नहीं ।
स्थिति III. यदि n = 3q + 2
∵n=3q+2 को 3 से विभाजित करने पर शेषफल 2 प्राप्त होता है । इसलिए n, 3 से विभाजित नहीं है ।
तथा n=3q+2 ⇒ n+2=(3q+2)+2=3(q+1)+1
⇒(n+2) को 3 से विभाजित करने पर शेषफल, 1 प्राप्त होता है ।
⇒(n+2),3 से विभाजित नहीं है ।
तब n=3q+2 ⇒ n+4=(3q+2)+4=3(q+2) ⇒ (n+4),3 से विभाजित है ।
∴ इस स्थिति में (n + 4), 3 से विभाजित है परन्तु n तथा n + 2 नहीं |
Topper's Solved these Questions
- वास्तविक संख्याऐंBOOK - BALAJI PUBLICATIONCHAPTER - वास्तविक संख्याऐंEXERCISE - विविध उदाहरण
9 Videos
- वास्तविक संख्याऐंBOOK - BALAJI PUBLICATIONCHAPTER - वास्तविक संख्याऐंEXERCISE - अतिलघु उत्तरीय प्रश्न
24 Videos
- रचनाऐBOOK - BALAJI PUBLICATIONCHAPTER - रचनाऐEXERCISE - स्वमूल्यांकन परिक्षण
2 Videos
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
Similar Questions
पूर्णांक a व 3 के लिए, अद्वितीय पूर्णांक q व r का अस्तित्व इस प्रकार है की a = 3q + r, तब r के संभावित मान ज्ञात कीजिए ।
View Solution1152 व 1664 को पूर्णतया विभाजित करने वाली सबसे बड़ी संख्या ज्ञात कीजिए ।
View Solution5.6 सेमी का रेखाखण्ड खींचकर उसे 5:8 के अनुपात में अन्तः विभक्त कीजिए
View Solutionदिये गये चित्र में TAB, O केंद्र वाले वृत्त की छेदक रेखा है तथा वृत्त के बिन्दु P पर TP एक स्पर्शी है। यदि TP = 5.6 सेमी तथा TA = 2.8 सेमी हो तब जीवा AB की माप ज्ञात कीजिए ।
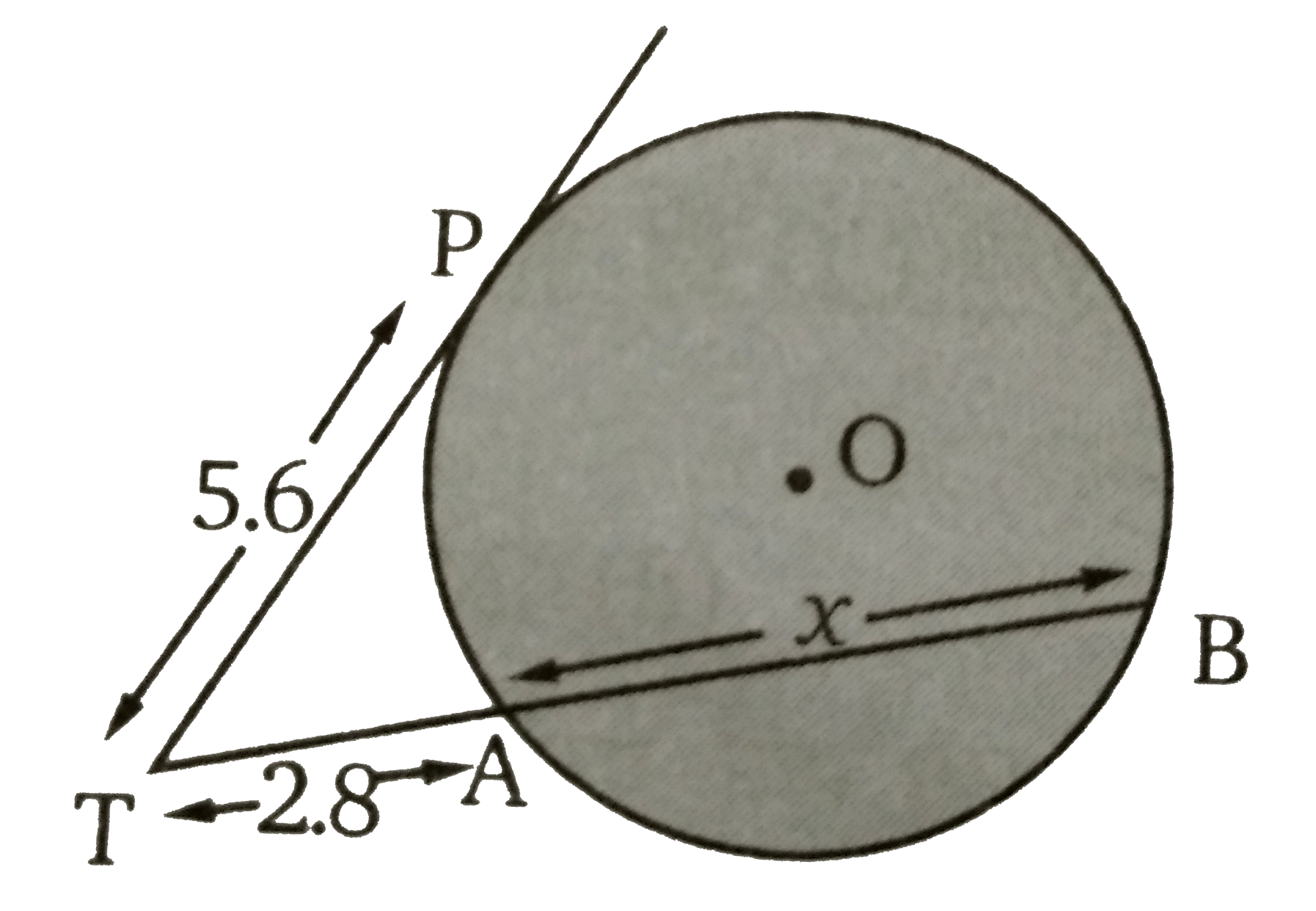
View Solutionयदि n एक धनात्मक पूर्णांक हो, तो निम्न में से कौन-सा संबंध असत्य है -
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionबताएं कि एक प्रतिदर्श समष्टि का विभाजन एक है या एक से अधिक?
View Solutionनिम्न कथन पर विचार कीजिये ''P(n)=n2−n+41 एक अभाज्य संख्या है'' तो इनमे से कौन-सा एक सत्य है?
View Solutionसदिश →a,→b,→c एक ही समतल में हैं। निम्न में से कौन-सा असत्य है?
View Solutionयदि cot x-tan x = 2 है, तो व्यापक हल है (यहाँ, n एक पूर्णांक है)
View Solutionदिखाइए कि अनुक्रम जिसका n वाँ पद 2n2+n+1 है, एक A.P. नहीं है।
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View SolutionN solid metallic spherical balls are melted and recast into a cylindrical rod whose radius is 3 times that of a spherical ball and height is 4 times the radius of a spherical ball. The value of N is :
N ठोस धात्विक गोलाकार गेंदों को पिघलाकर एक बेलनाकार छड़ बनाया जाता है जिसकी त्रिज्या एक गोलाकार गेंद की त्रिज्या से तिगुनी है और ऊंचाई एक गोलाकार गेंद की त्रिज्या से चोगुनी है |N का मान है :
View SolutionSOCl_2+HOHto[X]+[Y] निम्नलिखित में से कौन सा कथन गलत है/हैं? (I) उत्पादों में से एक गैस है जिसमें sp3d संकरण होता है। (II) दोनों उत्पाद प्रबल अम्ल होते हैं। (III) उत्पादों में से एक में Ppi-dpi बंध होता है। (IV) उत्पाद में से एक NH_3 के साथ अभिक्रिया करने पर श्वेत धूम देता है।
View Solutionहाइड्रोजन परमाणुओं में n = 4 से n = 2 संक्रमण के संगत विकिरण एक निश्चित धातु (कार्य फलन = 2.0 eV) पर गिरती है। फोटोइलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा होगी:
View Solutionएक परमाणु के बोर मॉडल में, जब एक इलेक्ट्रॉन n = 1 से n = 3 में कूदता है, तो कितनी ऊर्जा अवशोषित होगी?
View Solution
