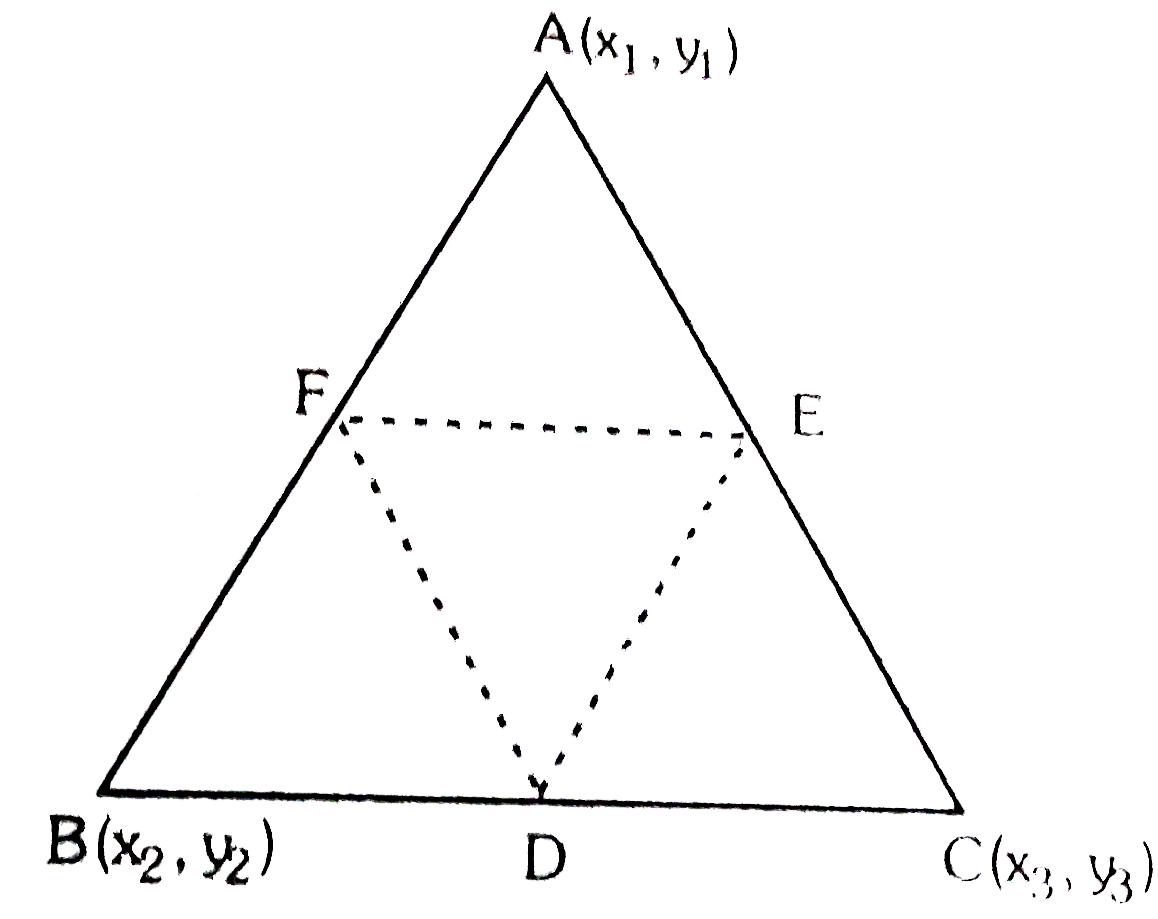
सिद्ध कीजिए कि किसी त्रिभुज का केन्द्रक वही है जो उसकी भुजाओं के मध्य बिंदुओं को मिलाने से बने त्रिभुज का होता है |
माना के शीर्ष तथा है | इसके केन्द्रक के निर्देशांक
प्रश्नानुसार, माना D,E,F क्रमशः भुजाओं BC,CA तथा AB के मध्य बिन्दु है |
तब,
अब का केन्द्रक
स्पष्टतः व एक ही बिन्दु को व्यक्त करते है |
Topper's Solved these Questions
- समकोणीय कार्तीय निर्देशांक निकाय BOOK - BALAJI PUBLICATIONCHAPTER - समकोणीय कार्तीय निर्देशांक निकाय EXERCISE - अभ्यास प्रश्न 13.1
22 Videos
- समकोणीय कार्तीय निर्देशांक निकाय BOOK - BALAJI PUBLICATIONCHAPTER - समकोणीय कार्तीय निर्देशांक निकाय EXERCISE - NCERT प्रारूप प्रश्न
4 Videos
- शंकु परिच्छेदः वृतBOOK - BALAJI PUBLICATIONCHAPTER - शंकु परिच्छेदः वृतEXERCISE - स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )
3 Videos
- समुच्चय BOOK - BALAJI PUBLICATIONCHAPTER - समुच्चय EXERCISE - विवेचनात्मक सोच वाले प्रश्न
5 Videos
Similar Questions
एक आयत के तीन शीर्ष (0,0)(2,0) तथा (0,3) है | सिद्ध कीजिए चौथे शीर्ष के निर्देशांक (2,3) होंगे |
View Solutionकार्तीय तल में एक चतुर्भुज जिसके शीर्ष (−4,5),(0,7),(5,−5) और (−4,−2) है | इसका क्षेत्रफल भी ज्ञात कीजिए |
View Solutionसिद्ध कीजिए की तीन वृतों x2+y2−4x−6y−12=0, x2+y2+2x+4y−10=0 तथा x2+y2−10x−16y−1=0 के केंद्र संरेखाय हैं।
View Solutionदो परिमित समुच्चों m में n है, प्रथम समुच्चय के उपसमुच्चायों की कुल संख्या, द्वितीय समुच्चय के उपसमुच्चयों से 56 अधिक है, m व n के मान ज्ञात कीजिए।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionत्रिभुज का गुरुत्व केंद्र होता है।
View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
View Solutionबिंदुओं (0,0),(0,8) और (4,6) से बने त्रिभुज का केन्द्रक और परिकेन्द्र ज्ञात कीजिए ।
View Solutionबिंदुओं (−3,−1),(−1,3) और (6,2) से बने त्रिभुज के परिकेन्द्र के निर्देशांक ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solution
