R त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवत्ति से घूर्णन कर रहा हैं । यह दर्शाइए कि इस तार में डाली कोई मणिका ω≤√g/R के लिए अपने निम्नतम बिंदु पर रहती हैं । ω=√2g/R के लिए , केंद्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता हैं ( घर्षण को उपेक्षणीय मानिए )
माना किसी क्षण मणिका स्थिति P में इस प्रकार है कि मणिका को तार के केंद्र से मिलाने वाला स्थिति सदिश ऊर्ध्वाधर से θ कोण बनाता हैं । यदि लम्बवत् प्रतिक्रिया N हैं , तब बिंदु P पर कार्यरत् विभिन्न बल ,
(i) मणिका का भार mg ( ऊर्ध्वाधर नीचे की ओर )
(ii) वृत्तीय तार की लम्बवत् प्रतिक्रिया केंद्र की ओर कार्य करती हैं । इसे क्षैतिज घटक Ncosθ में वियोजित किया जा सकता हैं ।
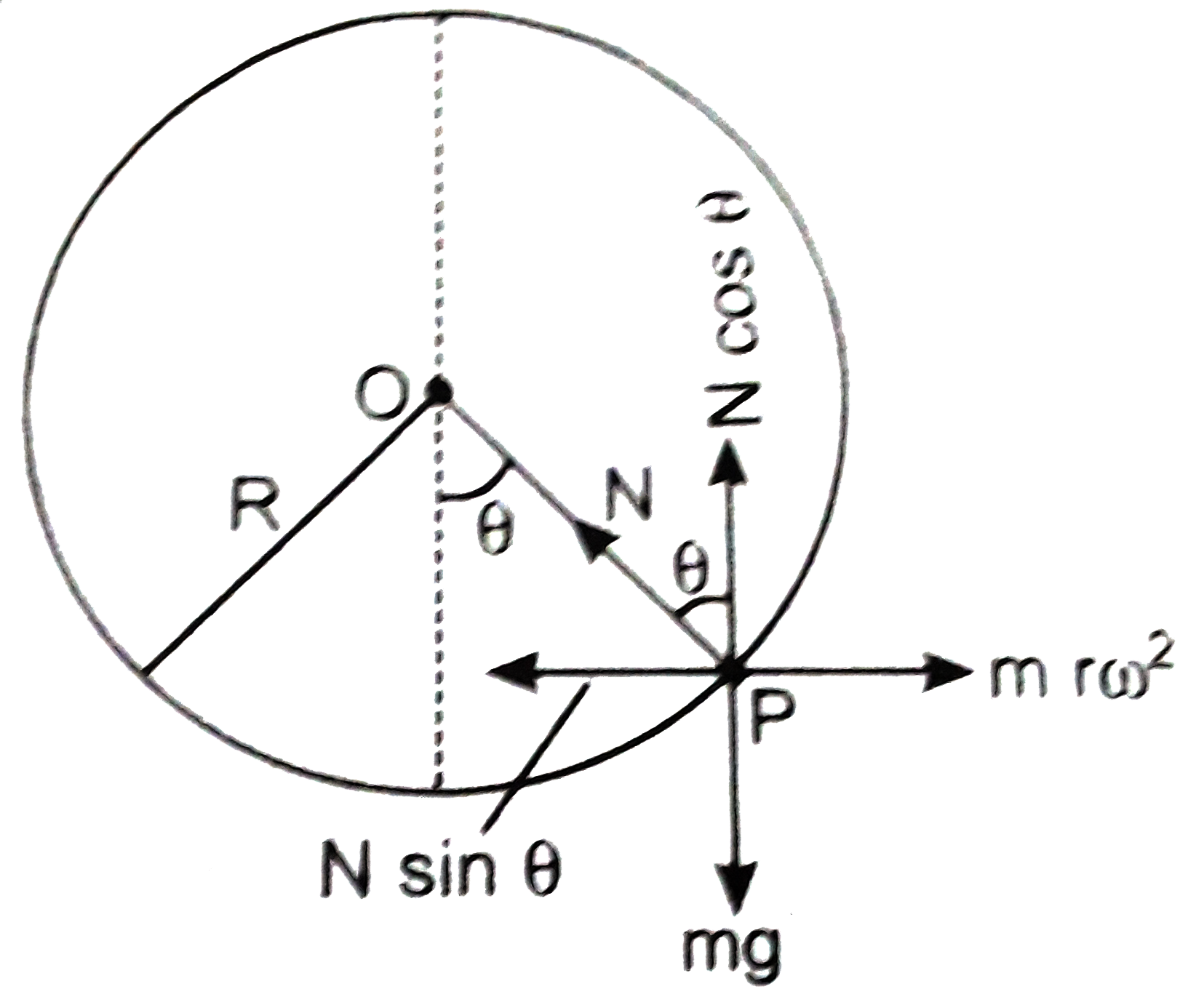
संतुलन की स्थिति में , mg=Ncosθ ..(i)
तथा mrω2=Nsinθ ...(ii)
परंतु क्षैतिज वृत्त की त्रिज्या r=Rsinθ
m(Rsinθ)ω2=Nsinθ
या mRω2 ..(iii)
N का मान समीकरण (iii) से समीकरण (i) में रखने पर , mg=mRω2cosθ या cosθ=gRω2 ..(iv)
परंतु cosθ≤1, अतः मणिका अपने निम्नतम बिंदु पर रहेगी ।
gRω2≤1 या ω≤√gR
तब ω=√2gR
समीकरण (iv) से , cosθ=gR×2g/R=12=cos60∘
या θ=60∘
Topper's Solved these Questions
- वृत्तीय गति की गतिकी BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तीय गति की गतिकी EXERCISE - आँकिक प्रश्न (आत्म - निरीक्षणात्मक )
8 Videos
- विस्पंद BOOK - BALAJI PUBLICATIONCHAPTER - विस्पंद EXERCISE - बहुविकल्पीय प्रश्न
15 Videos
- सदिश विश्लेषण BOOK - BALAJI PUBLICATIONCHAPTER - सदिश विश्लेषण EXERCISE - बहुकल्पीय प्रश्न
37 Videos
Similar Questions
0.1 किग्रा द्रव्यमान का एक पिण्ड 1 मीटर व्यास के वृत्ताकार मार्ग पर 31.4 सेकण्ड में 10 चक्कर की दर से घूम रहा हैं । पिण्ड पर लगने वाले अभिकेंद्र बल की गणना कीजिए ।
View Solution380 तथा 384 हर्ट्ज आवृत्ति के दो स्वरित्र 4 विस्पंद प्रति सेकण्ड उत्पन्न करते हैं। ध्वनि की अधिकतम तीव्रता के कितने समय बाद न्यूनतम तीव्रता सुनी जायेगी?
View Solutionनिम्न में कौन सी अदिश राशि है ?
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए निम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे। उपर्युक्त अवतरण किस एकांकी से लिया गया है और उसके लेखक कौन हैं ?
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे। किरोड़ीमल को किससे क्षमा माँगने के लिए कहा गया है ?
View Solutionसूरदास' के पद के आधार पर लिखिए कि गोपियों ने किन उदाहरणों के माध्यम से उद्धव को उलाहने दिए हैं।
View Solutionउत्साह' कविता में कवि बादल को गरजने के लिए क्यों कहता है? बादल से कवि की अन्य अपेक्षाएँ क्या हैं?
View Solutionअपने बैंक के प्रबंधक को पत्र लिखकर अपने आधार कार्ड को बैंक खाते से जोड़ने का अनुरोध कीजिए।
View Solutionनिर्देश : नीचे दिए गए गद्यांश को ध्यानपूर्वक पदिए और उस पर आधारित प्रश्नों के उत्तर दीजिए। बच्चे और खिलौने का सम्बन्ध सदैव से ही रहा है। हम यह भी कह सकते हैं कि खिलौनों के बिना हम बच्चों की दुनिया की कल्पना भी नहीं कर सकते। चाहे हम बच्चों को खिलौने खरीदकर दें या न दें, बच्चे अपने लिए किसी-न-किसी चीज़ (चाहे वे टूटे-फूटे डिब्बे हों या इसी तरह की अन्य सामग्री) को खिलौने की शक्ल दे ही देते हैं। बच्चों को एकदम छुटपन से ही मुँह से या खिलौनों से अजीबों-गरीब आवाजें निकालकर हम बहलाते हैं और बच्चे बहल भी जाते हैं। यही बच्चे जैसे-जैसे बड़े होते हैं, खुद भी चीज़ों को जोड़-तोड़कर खिलौने बनाने में अपनी रचनात्मक ऊर्जा का खूब इस्तेमाल करते हैं। इसलिए भी यह जरूरी हो जाता है कि बच्चों की इस रचनात्मक ऊर्जा को उभारने के लिए उन्हें भरपूर मौके दिए जाएँ। पहले हम गौर करें कि बच्चे अपने रोजमर्रा के जीवन में । कौन-कौन-सी चीजें बनाते हैं? इसके लिए अगर हम अपने अतीत में गोता लगाएँ और अपने बचपन की दुनिया में झाँकें, तो तरह-तरह के खिलौनों का खजाना हमारी स्मृति में से निकलकर आता है-ढेर सारी माचिस की खाली डिब्बियों को बिल्कुल सरल तरीके से जोड़कर बनती रेलगाड़ी, कागज़ से बनाई जाने वाली ढेरों चीजें जैसे नाव, हवाई जहाज, तितली, नाग आदि क्या-क्या नहीं बनाते थे, इन सब से। निम्नलिखित में से कौन-सी चीज़ बच्चे के लिए दूरबीन बन सकती है?
View Solutionनिर्देश : नीचे दिए गए गद्यांश को ध्यानपूर्वक पदिए और उस पर आधारित प्रश्नों के उत्तर दीजिए।
बच्चे और खिलौने का सम्बन्ध सदैव से ही रहा है। हम यह भी कह सकते हैं कि खिलौनों के बिना हम बच्चों की दुनिया की कल्पना भी नहीं कर सकते। चाहे हम बच्चों को खिलौने खरीदकर दें या न दें, बच्चे अपने लिए किसी-न-किसी चीज़ (चाहे वे टूटे-फूटे डिब्बे हों या इसी तरह की अन्य सामग्री) को खिलौने की शक्ल दे ही देते हैं।
बच्चों को एकदम छुटपन से ही मुँह से या खिलौनों से अजीबों-गरीब आवाजें निकालकर हम बहलाते हैं और बच्चे बहल भी जाते हैं। यही बच्चे जैसे-जैसे बड़े होते हैं, खुद भी चीज़ों को जोड़-तोड़कर खिलौने बनाने में अपनी रचनात्मक ऊर्जा का खूब इस्तेमाल करते हैं। इसलिए भी यह जरूरी हो जाता है कि बच्चों की इस रचनात्मक ऊर्जा को उभारने के लिए उन्हें भरपूर मौके दिए जाएँ।
पहले हम गौर करें कि बच्चे अपने रोजमर्रा के जीवन में । कौन-कौन-सी चीजें बनाते हैं? इसके लिए अगर हम अपने अतीत में गोता लगाएँ और अपने बचपन की दुनिया में झाँकें, तो तरह-तरह के खिलौनों का खजाना हमारी स्मृति में से निकलकर आता है-ढेर सारी माचिस की खाली डिब्बियों को बिल्कुल सरल तरीके से जोड़कर बनती रेलगाड़ी, कागज़ से बनाई जाने वाली ढेरों चीजें जैसे नाव, हवाई जहाज, तितली, नाग आदि क्या-क्या नहीं बनाते थे, इन सब से।
बच्चों की रचनात्मक ऊर्जा को उभारने के लिए
View SolutionM, N, P, R, T, W, F and H are sitting around a circle at the centre, P is third to the left of M and second to the right of T. N is second to the right of P. R is second to the right of W who is second to the right of M. F is not an immediate neighbour of P. Who is to the immediate right of P?
M, N, P, R, T, W, F और H केंद्र में एक वृत्त के चारों ओर बैठे हैं,P, M के बाएं से तीसरे और T के दायें से दूसरे स्थान पर हैं| N, Pके दाईंओर दूसरा है। R, W के दायें से दूसरे नंबर पर है, जो M के दायें से दूसरे नंबर पर है, P का तत्काल पड़ोसी नहीं है। P के तत्काल दाएं को कौन है?
View Solutionनिम्नलिखित में से कौन सी रेखाएँ, एक ऊष्माक्षेपी अभिक्रिया के लिए, साम्यावस्था स्थिरांक K की तापमान पर निर्भरता को सही ढंग से प्रदर्शित करती हैं?
View Solutionनिम्न में से कुछ विधियाँ हैं जो आमतौर पर धातुओं के उनके अयस्कों से निष्कर्षण के लिए उपयोग होती हैं। सोडियम के निष्कर्षण के लिए आमतौर पर निम्न में से कौनसी विधि उपयोग में लायी जाती है?
View Solutionप्रोपेनॉल को प्रोपेन में परिवर्तित करने के लिए उपयोग किया जाने वाला अभिकर्मक है(हैं):
View Solutionप्रोपेनॉल को प्रोपेन में परिवर्तित करने के लिए उपयोग किया जाने वाला अभिकर्मक है(हैं):
View Solutionइस गद्य को ध्यान से पढ़े और नीचे दीए गए प्रश्न का उत्तर देः
हम परोपकार कई प्रकार से कर सकते हैं। हम धन के बल पर दुसरों का हीत कर सकते हैं। भूखे को रोटी खिला सकते हैं नंते का दन ढकने के लिए वस्त्र दै सकते हैं ।धर्मशालाएं बनवा सकतै हैं गरीबों के उपचार के औषधालय बनवा सकते हैं । यदि हम प्रभु की कृपा से धन से वंचित हैं, तो तनःमन से भी दुसरों की भलाई कर सकते ही अशिक्षिततों को शिक्षा दे सकते हैं । वास्तव में देखा जाए तो यही सच्चा दान है । इससे मानव अपने और परिवार के लिए कुछ सुखःशान्ति प्राप्त कर सकते हैं इससे प्राप्त धन से बच्चो का पेट पल सकता है इसके अतिरिक्त शारीरीक शक्ति द्वारा भी परकोप किया जा सकता है। भूलैःभटके को राह दीखला सकते हैं प्यासे को पानी पिला सकते हैं अबलओ की रक्षा कर सकते हैं ।
प्नश्नः धन के बल पर हम क्या कर सकते है ?
View Solution
