चित्र में कुछ एकविमीय स्थितिज ऊर्जा-फलानो के उदहारण दिये गये हैं। कण की कुल ऊर्जा कोटि-अक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए,यदि कोई है तो, जिनमे दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता है। इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हो।
किसी वस्तु की कुल ऊर्जा, उस वस्तु की गतिज ऊर्जा तथा स्थिति ऊर्जा के योग के बराबर होती है। अतः
E=KE+PE
⇒KE=E−PE
किसी वस्तु की गतिज ऊर्जा त्रणात्मक नहीं हो सकती है तथा किसी भी वस्तु की स्थितिज ऊर्जा से अधिक नहीं हो सकती है अर्थात कण ऐसे क्षेत्र में प्रवेश नहीं कर सकता है, जहाँ इसकी गतिज ऊर्जा त्रणात्मक या स्थितिज ऊर्जा कुल ऊर्जा से अधिक होगी। यदि कण की कुल ऊर्जा न्यूनतम होगी यदि गतिज ऊर्जा शून्य है।
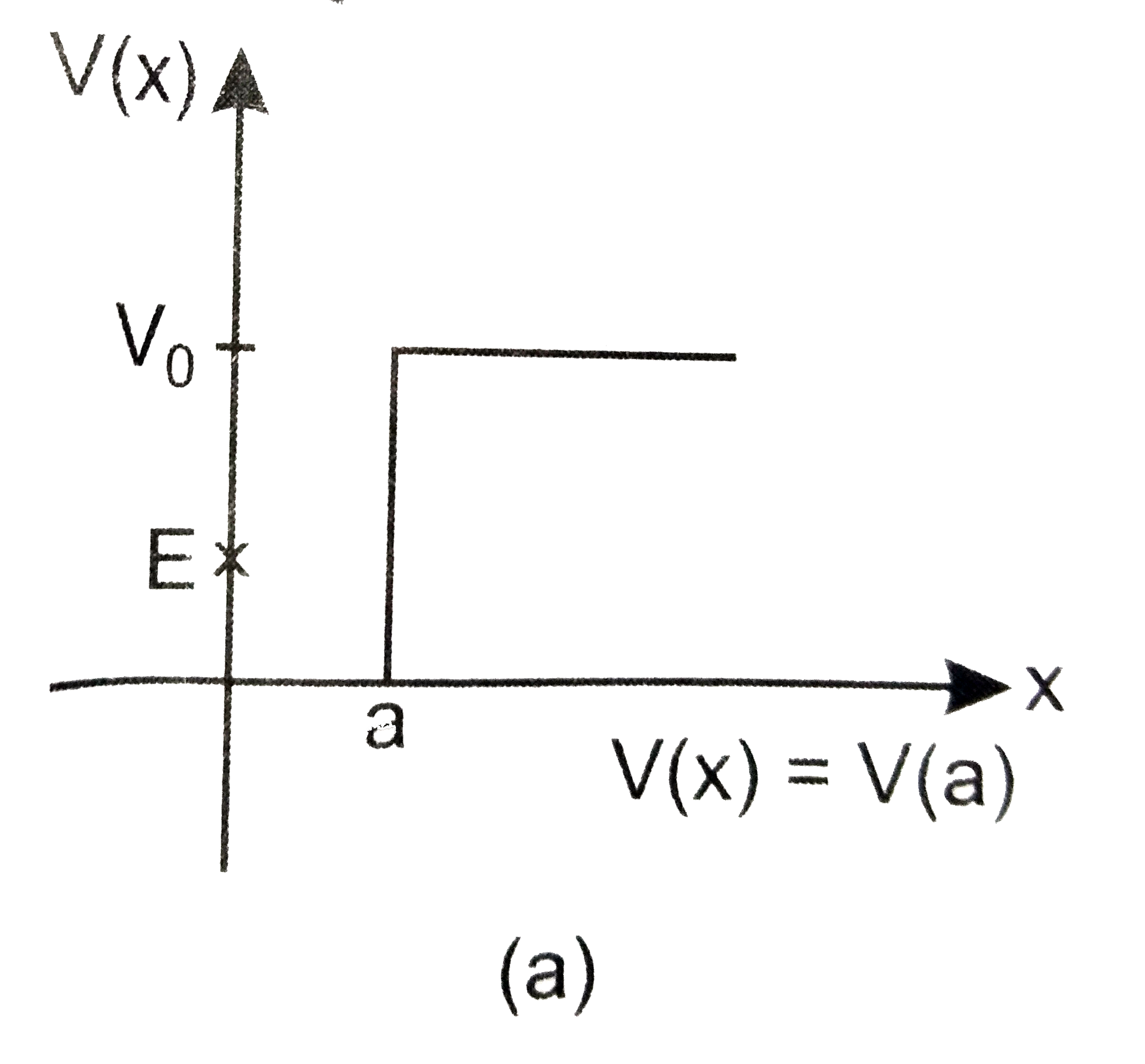
(i) क्षेत्र x=0 से x=a तक स्थितिज ऊर्जा शून्य है इसलिए गतिज ऊर्जा धनात्मक होगी। अतः कण इस क्षेत्र में पाया जा सकता है। इस स्थिति में कण की न्यूनतम कुल ऊर्जा शून्य है (ली गई गतिज ऊर्जा शून्य है)।
क्षेत्र (x>a) में, स्थतिज ऊर्जा, कुल ऊर्जा से अधिक है इसलिए इस क्षेत्र में गतिज ऊर्जा त्रणात्मक है। अतः कण इस क्षेत्र (x>a) में नहीं पाया जा सकता है।
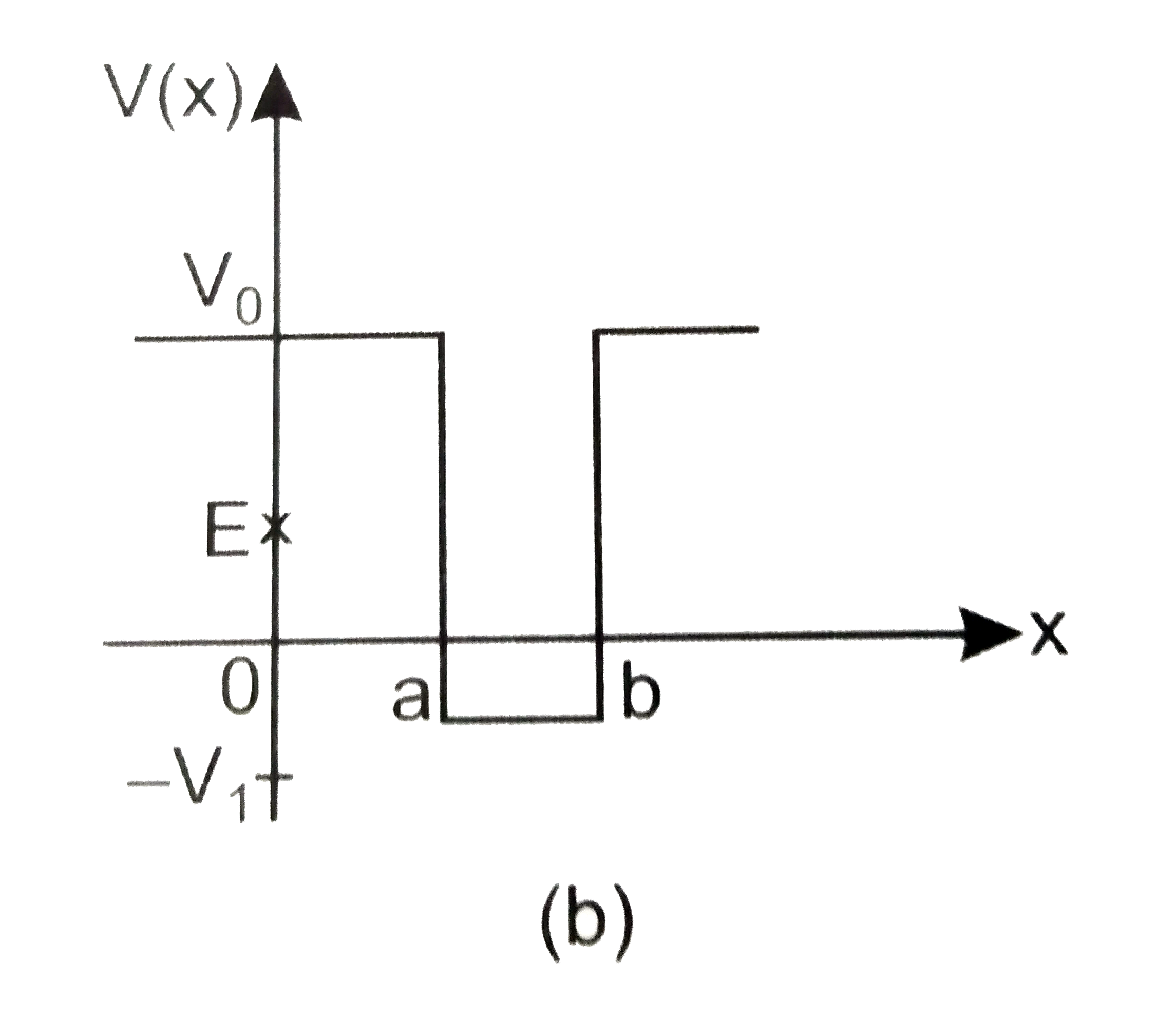
(ii) क्षेत्र (x<a तथा x>b) में हम देख सकते है, की स्थतिज ऊर्जा कुल ऊर्जा E से अधिक है, इसलिए गतिज ऊर्जा त्रणात्मक होगी (∵KE=E−PE) अतः कण इस क्षेत्र में नहीं पाया जा सकता है क्षेत्र (x<a) तथा (x>b) में हम देख सकते है की स्थितिज ऊर्जा त्रणात्मक है इसलिए गतिज ऊर्जा धनात्मक है। (∵ गतिज ऊर्जा = कुल ऊर्जा - स्थितिज ऊर्जा) अतः कण इस क्षेत्र में नहीं पाया जाता है।
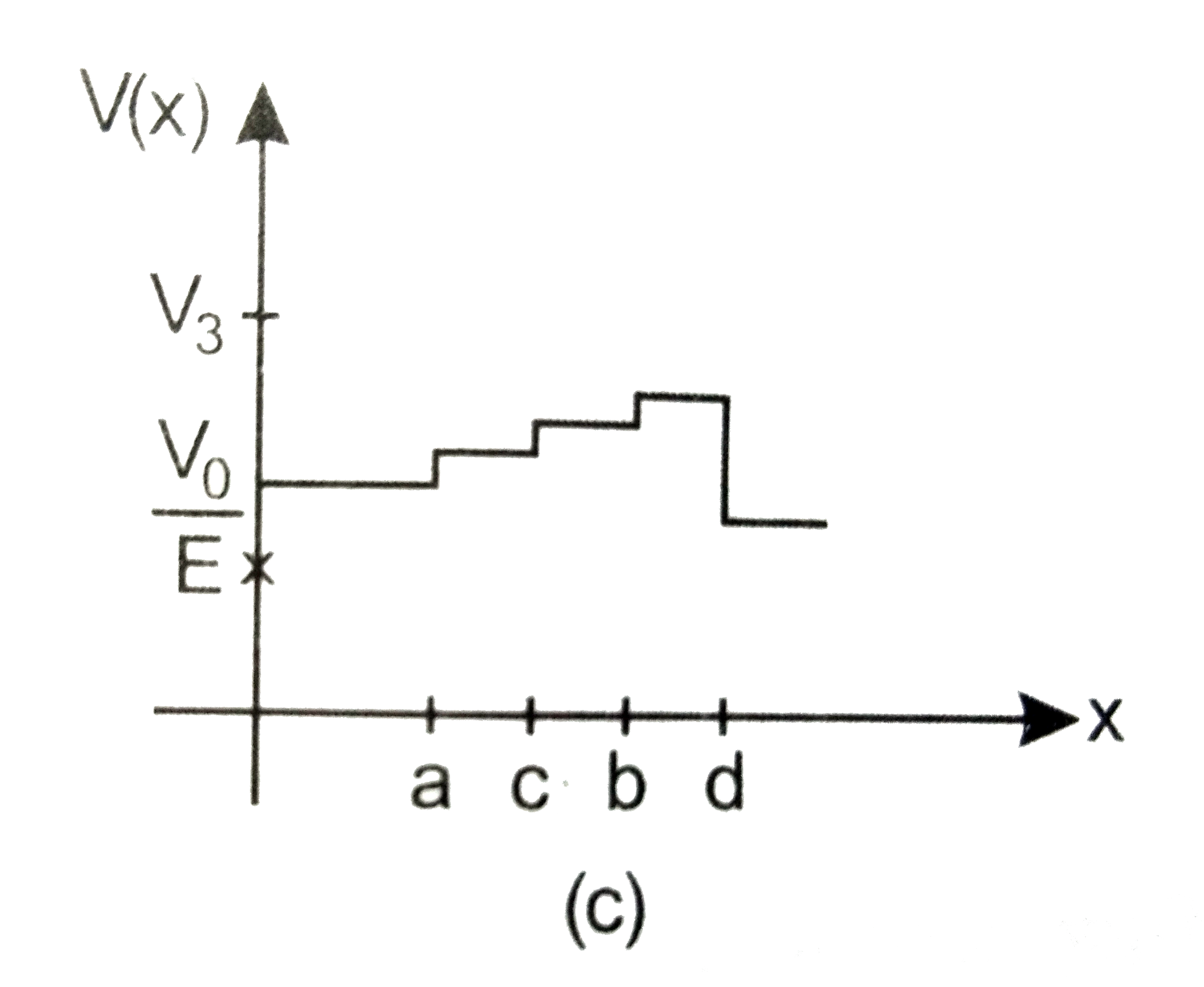
(iii) इन सभी क्षेत्रो (x>0) में, स्थितिज ऊर्जा कुल ऊर्जा से अधिक है, इसलिए गतिज ऊर्जा त्रणात्मक होगी। अतः कण इन सभी क्षेत्रों (x>0) में नहीं पाया जा सकता है। इस स्थिति में कण की कुल न्यूनतम ऊर्जा v1 होगी।
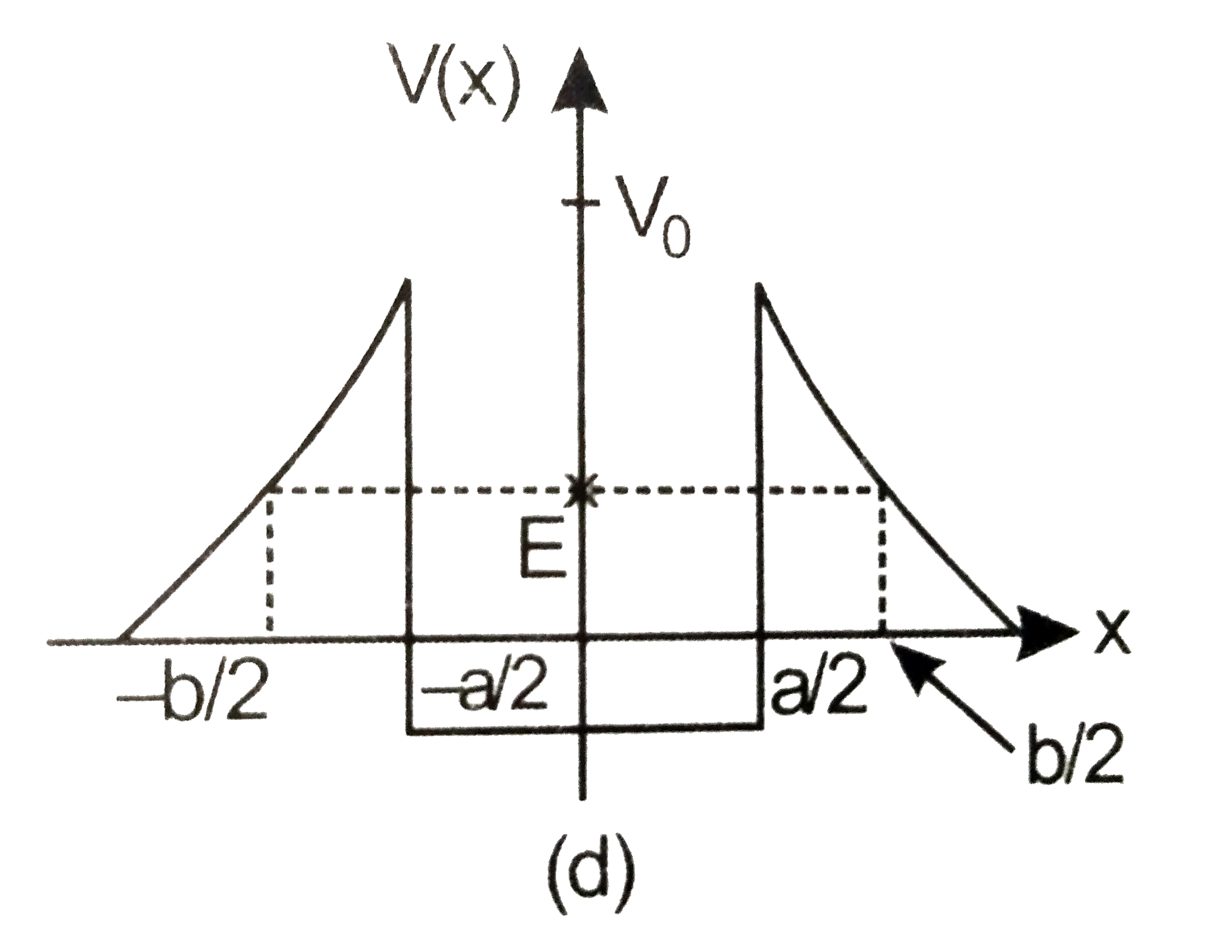
−b2<x<−a2 तथा a2<x<b2 में स्थतिज कुल ऊर्जा से अधिक है। इसलिए गतिज ऊर्जा त्रणात्मक होगी। अतः कण इन क्षेत्रों में नहीं पाया जा सकता है। क्षेत्र x<−b2 और x>b2 में भी स्थतिज ऊर्जा त्रणात्मक है तथा स्थतिज ऊर्जा कुल ऊर्जा से कम है। इसलिए इन सभी क्षेत्रों में गतिज ऊर्जा धनात्मक होगी। अतः कण इन क्षेत्रों में पाया जा सकता है। इस स्थिति में कण की कुल न्यूनतम ऊर्जा −U1 होगी।
Topper's Solved these Questions
- कार्य, ऊर्जा, शक्ति एव संघट्ट BOOK - BALAJI PUBLICATIONCHAPTER - कार्य, ऊर्जा, शक्ति एव संघट्ट EXERCISE - अतिरिक्त अभ्यास
7 Videos
- कार्य, ऊर्जा, शक्ति एव संघट्ट BOOK - BALAJI PUBLICATIONCHAPTER - कार्य, ऊर्जा, शक्ति एव संघट्ट EXERCISE - बहुविकल्पीय प्रश्न
35 Videos
- ऊष्मागतिकी का शून्य कोटि एवं प्रथम नियम BOOK - BALAJI PUBLICATIONCHAPTER - ऊष्मागतिकी का शून्य कोटि एवं प्रथम नियम EXERCISE - बहुविकल्पीय प्रश्न
37 Videos
- गुरुत्वाकर्षण -1 BOOK - BALAJI PUBLICATIONCHAPTER - गुरुत्वाकर्षण -1 EXERCISE - बहुविकल्पीय प्रश्न
36 Videos
Similar Questions
0.012 किग्रा द्रव्यमान कि कोई गोली 70 मीटर/सेकण्ड कि क्षैतिज चाल से चलते हुए 0.4 किग्रा द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरंत ही विरामावस्था में आ जाती है। गुटके को छत से पतली तारो द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है। ? गुटके के पैदा हुई ऊष्मा कि मात्रा भी अनुमान लगाइए।
View Solutionकिसी बल द्वारा कृत कार्य हो सकता है-
View Solutionकोन-सा कथन असत्य है
View Solutionदीर्घवृताकार कक्षा में किसी गृह की चाल
View Solutionवैद्युत क्षेत्र में वैद्युत द्विध्रुव | बाह्य क्षेत्र में द्विध्रुव की स्थितिज ऊर्जा
View Solutionसमविभव पृष्ठ | आवेशों के निकाय की स्थितिज ऊर्जा | एकल आवेश की स्थितिज ऊर्जा
View Solutionस्थितिज ऊर्जा | किसी ऊँचाई पर वस्तु की स्तिथिज ऊर्जा
View Solutionस्थिरवैद्युत स्थितिज ऊर्जा, || बाह्य क्षेत्र में द्विध्रुव की स्थितिज ऊर्जा
View Solutionआवेशित चालक की स्थितिज ऊर्जा || आवेशित संधारित्र की स्थितिज ऊर्जा
View Solutionऊर्जा के विभिन्न रूप | यांत्रिक ऊर्जा |गतिज ऊर्जा तथा स्थितिज ऊर्जा | संवेग और गतिज ऊर्जा में सम्बन्ध |किसी स्प्रिंग की स्थितिज ऊर्जा
View Solutionतरलों के यांत्रिकी गुण |प्रवाहित तरल की ऊर्जा #!#गतिज ऊर्जा #!#स्थितिज ऊर्जा#!#दाब ऊर्जा
View SolutionRecap|एक बिन्दु आवेश की स्थिति ऊर्जा |दो आवेशों की निकाय की स्थितिज ऊर्जा |वैधुत द्विध्रुव की स्थितिज ऊर्जा |OMR|Summary
View SolutionRevision|प्रश्न|स्थिर वैद्युत स्थितिज ऊर्जा|स्थिर वैद्युत अन्योन्य ऊर्जा|दो आवेशित कणो के निकाय की अन्योन्य ऊर्जा|आवेशित कणो के निकाय के लिये अन्योन्य ऊर्जा|OMR|Summary
View Solutionस्थितिज ऊर्जा #!#ऊंचाई पर स्थित वस्तु में ऊर्जा
View SolutionH-परमाणु की प्रथम कक्षा में एक इलेक्ट्रॉन की ऊर्जा −13.6eV है। Li2+ आयनों की बोर कक्षाओं में इलेक्ट्रॉनों के लिए उत्तेजित अवस्था में संभावित ऊर्जा मान है/हैं-
View Solutionहाइड्रोजन के समान एक काल्पनिक परमाणु के लिए, निकाय की स्थितिज ऊर्जा U (1) = (-ke^2)/(r^3) द्वारा दी जाती है, जहाँ r दो कणों के बीच की दूरी है। यदि कोणीय संवेग के क्वान्टीकरण का बोर मॉडल लागू होता है, तो कण का वेग निम्नलिखत में किसके द्वारा दिया जाता है?
View Solution
