(a) दर्शाइए की आवेशित पृष्ट के एक पाश्र्व से दूसरे पाश्र्व पर स्थिरवैघृत क्षेत्र के अभिलम्ब घटक में असांतत्य होता है, जिसे
(E2−E1).ˆn=σε0
द्वारा व्यक्त किया जाता है। यहाँ ˆn एक बिंदु पर पृष्ट के अभिलम्ब एकांक सदिश है तथा σ उस बिंदु पर पृष्ट आवेश धनत्व है (ˆn) की दिशा पाश्र्व 1 से पाश्र्व 2 की और है। अतः दर्शाइए की चालक की ठीक बाहर विघुत क्षेत्र σˆnε है।
(b) दर्शाइए की आवेशित पृष्ट के एक पाश्र्व से दूसरे पाश्र्व पर स्थिर वैघृत क्षेत्र का स्पर्शीय घटक संतत है।
(a) माना AB एक आवेशित पृष्ट है जिसके दो क्षेत्र चित्रानुसार दर्शाइए गए है, एक सिलिंडर में अलप आवेशित पृष्ट ΔS है, जो गौसियां पृष्ट है।
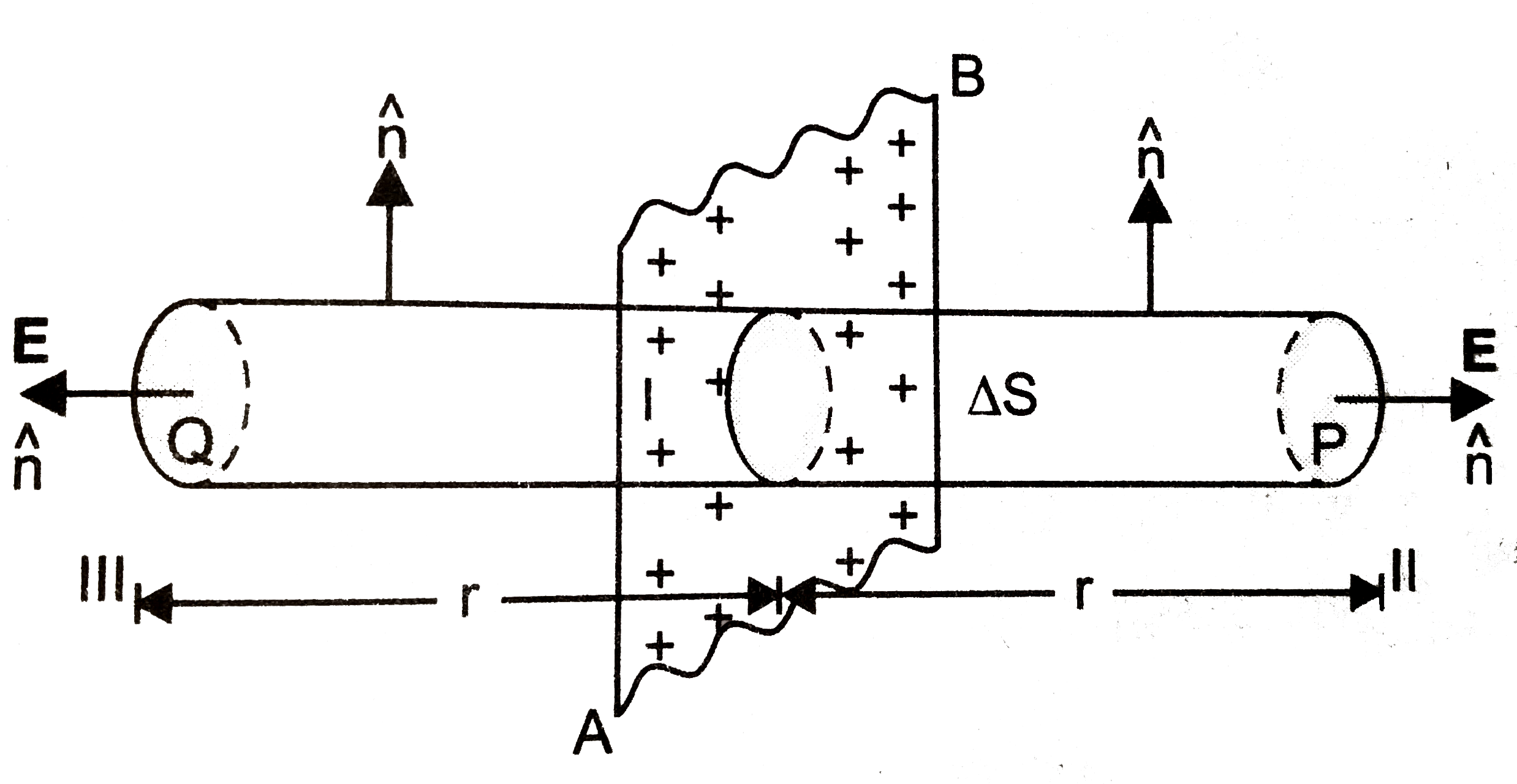
गाऊस प्रमेय के अनुसार, पृष्ट से होकर जाने वाला कुल वैघृत फ्लक्स
∮SA.dS=∮IA.dS+∮IIA.ds+∮IIIA.dS=σΔSε0
∮IIA1.dS+∮IIIEq.dS=σΔSε0∴θ=90∘∴cos90∘=0
or E1.ΔSˆn1+E2.ΔSˆn1=σε0ΔS
E1+E2
E1.ˆn1+E2.ˆn2=σε0
E1.(−ˆn2)+E2.ˆn2=σε0
(E2−E1).ˆn2=σε0
(E2−E1).ˆn=σε0.....................(i)
(∴ˆn2=ˆn)= पाश्र्व 1 व 2 की और एकांक सदिश)
चित्र से यह स्पष्ट है की E1 चालक के अंदर की और है। हम यह भी जानते है की चालक के अंदर वैघृत क्षेत्र शून्य होता है।
E2.ˆn=σε0
(E2−ˆn).ˆn=σε0ˆn
E2=σε0ˆn(∴ˆn.ˆn=1)
चालक से ठीक बाहर वैघृत क्षेत्र =σε0ˆn
वैघृत क्षेत्र के स्पष्ररिखीय घटक (एक आवेशित पृष्ट से दूसरे आवेशित पृष्ट पर) सतत है, एक बंद लूप का वैघृत क्षेत्र शून्य होता है। माना वैघृत क्षेत्र में ABA एक आवेशित पृष्ट है जिसके केंद्र पर आवेश q है। माना rA or rB क्रमश: बिंदु A व B पर धनात्मक सदिश है। माना बिंदु P पर वैघृत क्षेत्र E है, अतः Ecosθ वैघृत क्षेत्र E का स्पर्शरिखीय घटक है।

∴E.dI=Edl.cosθ=(Ecosθ)dl
∫BAE.dl=14πε0q.(1rA−1rB)
∫BAE.dl=14πε0q.(1rB−1rA)
∴∮AaBbaE.dl=∫BAE.dl+∫ABE.dl
=14πε0q.(1rA−1rB+1rB−1rA)
=0 यदि सिद्ध करना था
Topper's Solved these Questions
Similar Questions
5×10−8 C तथा −3×10−8 C के दो आवेश 16 सेमि० को दुरी पर स्थित हैं। दोनों आवेशों को मिलाने वाली रेखा के किस बिंदु पर वैघृत विभव शुन्य होगा? अनंत पर विभव शून्य लीजिये।
View Solutionव्योम तरंगों के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित आवृत्तियों में से कौन-सी उपयुक्त रहेगी ?
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionमंथन के पश्चात दूध को कपड़े के एक टुकड़े पर उढ़ेलने पर क्रीम उस पर रह जाता है। पृथक्करण की यह प्रक्रिया ...... कहलाती है।
View SolutionHeight of a tower is 120 metres. The angle of elevation of the top of tower from a point B is 75^@ .Point B is on the ground level. What is the distance (in metres)of point B from the base of tower? एक भीनार की ऊँचाई 120 मीटर है। बिंदु B से मीनार की चोटी का उन्नयन कोण 75^@ है। बिंदु B जमीन की सतह पर है। मीनार के आधार से बिंदु B की दूरी (मीटर में) क्या है?
View Solution'दरबार' कविता के माध्यम से किस पर अपनी तीखी प्रतिक्रिया । व्यक्त की है?
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solution
