बिंदु $(0, 0, - a)$ तथा (0,0,a) पर दो आवेश क्रमश: $- q$ और $+ q$ स्थित हैं।
(a) बिंदुओं (0,0,z) और (x,y,0) पर स्थिरवैघृत विभव क्या हैं?
(b) मूल बिंदु से किसी बिंदु की दुरी r पर विभव की निर्भता ज्ञात कीजिये, जबकि $r / a > > 1$ हैं।
( c) $x$ - अक्ष बिंदु (5,0,0) से बिंदु $(- 7, 0, 0)$ तक एक परिक्षण आवेश को ले जाने में कितना कार्य करना होगा? यदि परीक्षण आवेश के उन्ही बिंदुओं के बीच $x$ - अक्ष से होकर ने ले जाएँ तो क्या उत्तर बदल जायेगा।

Video Solution

Text Solution

Verified by Experts

यहाँ पर दो आवेश z-अक्ष पर स्थिति $(0, 0 - a)$ व $(0, 0, a)$ पर हैं। दोनों एक द्विध्रुव बनाते हैं, जिसकी लम्बाई 2a हैं। माना C के निर्देशांक (0,0,z) हैं तथा D के निर्देशांक $(x, y, 0)$ हैं।
(a) (0,0,z) पर विभव V हैं
V=A के कारण C पर विभव $+ B$ के कारण C पर विभव
$V = V_{A} + V_{B} = \frac{1}{4 π ε_{0}} . \frac{- q}{A C} + \frac{1}{4 π ε_{0}} . \frac{q}{B C}$
$= \frac{1}{4 π ε_{0}} [- \frac{q}{A O + O C} + \frac{q}{O C - B O}]$
$= \frac{q}{4 π ε_{0}} [- \frac{1}{z + a} + \frac{1}{z + a}] = \frac{q}{4 π ε_{0}} [\frac{- z + a + z + a}{z^{2} - a^{2}}]$
$= \frac{q .2 a}{4 π ε_{0} . (z^{2} - a^{2})}$
$= \frac{P}{4 π ε_{0} (z^{2} - a^{2})}$
बिंदु (x,y,0), z-अक्ष के सापेक्ष लंबवत हैं तथा हम जानते हैं कि द्विध्रुव कि आशीय रेखा पर विभव शून्य हैं।
(b) द्विध्रुव कि यादृच्छिक स्थिति में वैघृत विभव,
$V = \frac{1}{4 π ε_{0}} . \frac{p cos θ}{(r^{2} - a^{2} {cos}^{2} θ)}$
प्रश्नानुसार, यदि $r > > a$ , तब $r^{2}$ को $a^{2}$ कि तुलना में नगण्य मानने पर, वैघृत विभव
$V = \frac{p cos θ}{4 π ε_{0} . r^{2}}$
or $V \propto \frac{1}{r^{2}}$
( C) कृत कार्य= आवेश $\times$ [+q व $- q$ के कारण स्थिति (5,0,0) पर विभवांतर]
विभव $(V_{1}) = \frac{1}{4 π ε_{0}} . \frac{- q}{{\sqrt{5 - 0}}^{2} + {(0 - a)}^{2}} + \frac{1}{4 π ε_{0}} . \frac{q}{{\sqrt{5 - 0}}^{2} + {(a - 0)}^{2}}$
$= - \frac{q}{4 π ε_{0} \sqrt{a^{2} + 25}} + \frac{1}{4 π ε_{0} \sqrt{a^{2} + 25}} = 0$
स्थिति $(- 7, 0, 0)$ पर +q व $- q$ के कारण विभव
$V_{2} = \frac{1}{4 π ε_{0}} . \frac{- q}{{\sqrt{- 7 - 0}}^{2} + a^{2}} + \frac{1}{4 π ε_{0}} . \frac{q}{{\sqrt{- 7 - 0}}^{2} + a^{2}} = 0$
$∴$ कृत कार्य $= q (V_{2} - V_{1}) = q \times 0 = 0$
यहाँ कृत कार्य पथ पर निर्भर नहीं करता हैं अतः यदि पथ बदलता हैं तब कार्य (x-अक्ष के दो बिंदु पर) सैदेव शून्य होगा।

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

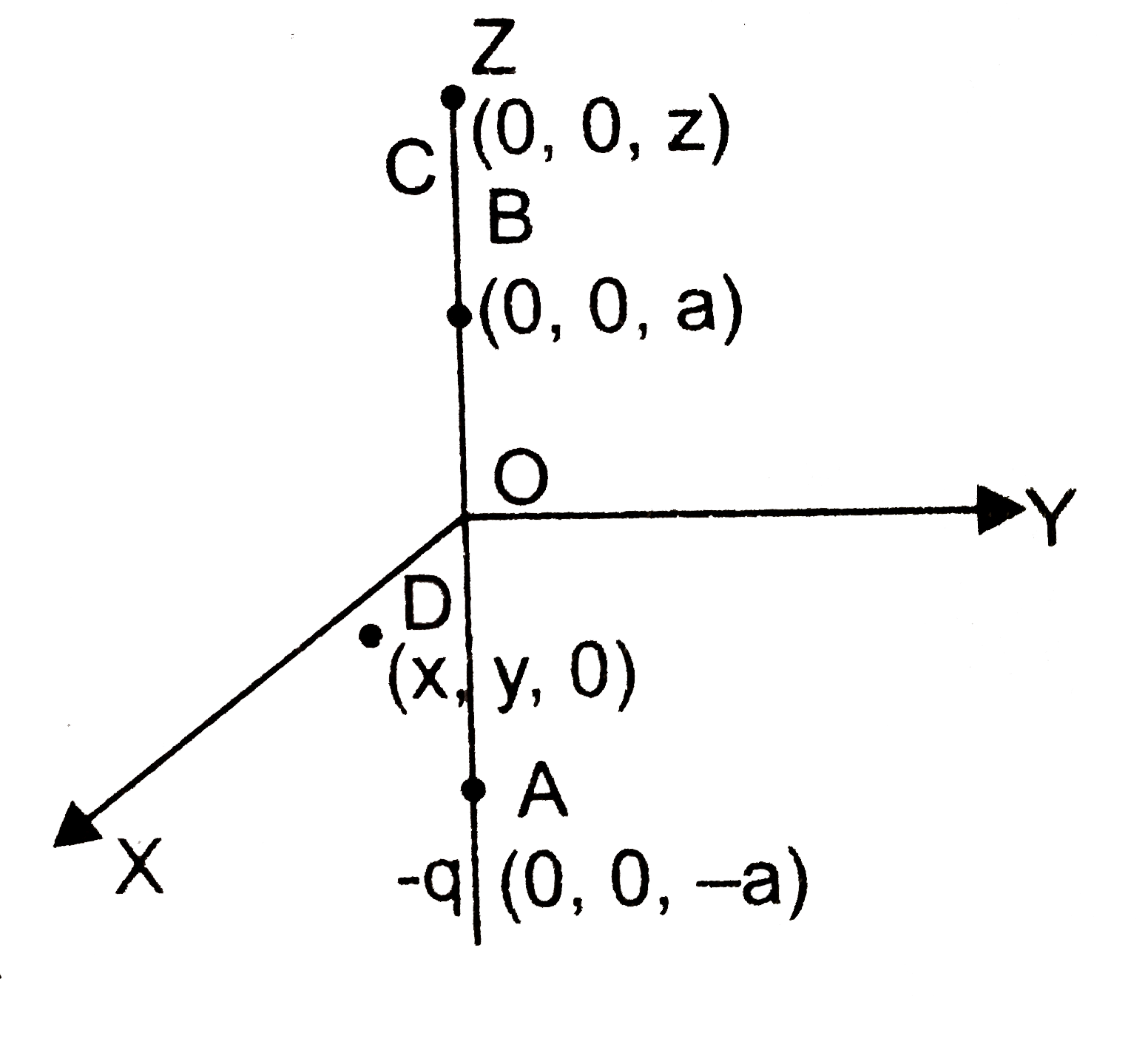
Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-स्थिर वैघुत विभव तथा धारिता -अतिरिक्त अभ्यास

Home
Ask Doubt
Profile