Question

दर्शाइए की एक समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका पर बल का परिमाण ${\displaystyle \frac{1}{2}QE}$ हैं, जहाँ Q संधारित्र पर आवेश हैं और E पट्टिकाओं के बीच विघुत क्षेत्र का परिमाण हैं। घटक ${\displaystyle \frac{1}{2}}$ के मूल को समझाइये।

Explanation

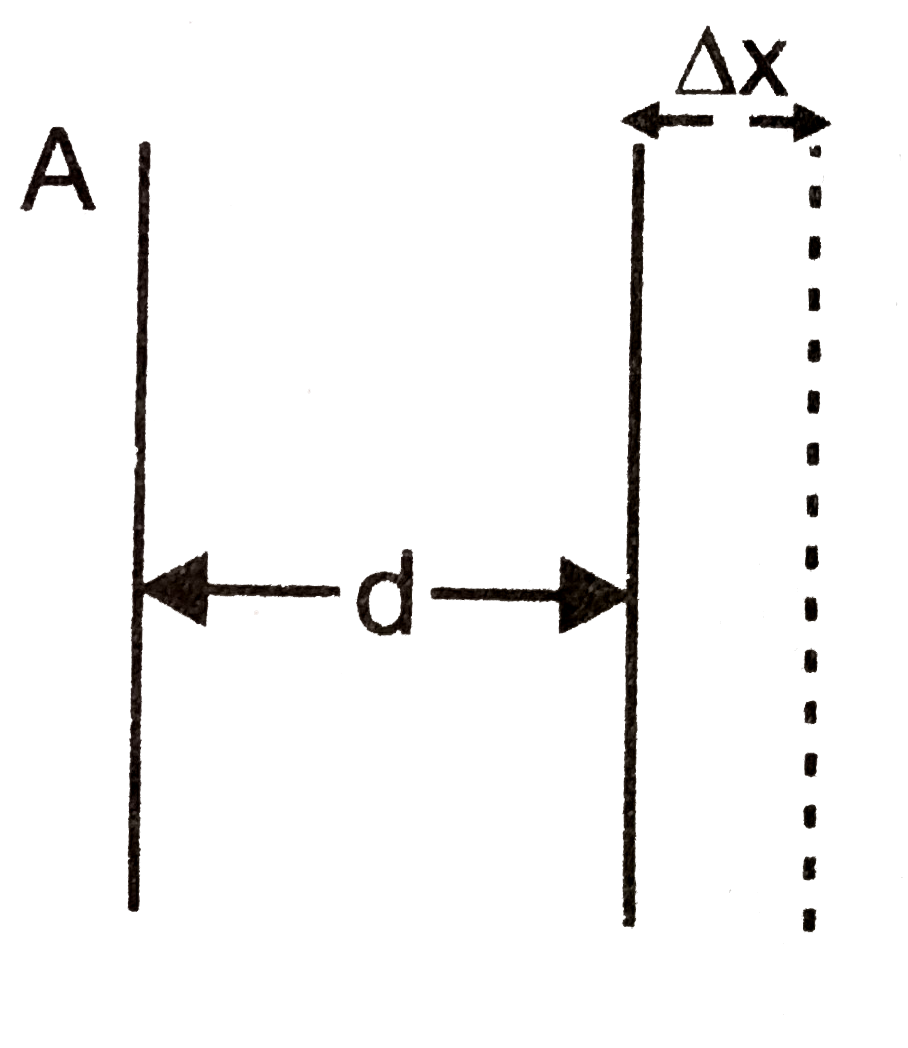
माना पट्टिकाओं के बीच की दुरी में अति सूक्षम वृद्धि `Deltax` होती हैं। प्रत्येक प्लेट पर बल F हैं। `Deltax` दुरी बढ़ाने में कृत कार्य = बल `xx` दुरी में वृद्धि
`=F.Deltax`…….(i)
संधारित्र के आयतन में वृद्धि =पट्टिकाओं का क्षेत्रफल `xx` बढ़ी हुई दुरी `=A. Deltax`
ऊर्जा धनत्व =u `=(ऊर्जा/आयतन)`
ऊर्जा = u `xx` आयतन `=u.A.Deltax`........(ii)
`therefore` ऊर्जा =कृत कार्य
`F.Deltax= u.A.Deltax` [समीकरण (i) or (ii)]
`=1/2epsilon_(0)E^(2).A (therefore u=1/2epsilon_(0)E^(2) or E=V/d)`
`=1/2epsilon_(0).V^(2)/d^(2).A`
`=(epsilon_(0)A)/d.V/d xx 1/2 (therefore C=(epsilon_(0)A)/(d), CV=q)`
`=1/2E.CV=1/2QE`
बल में `1/2` का घटक इस तथ्य दवा व्याख्या की जा सकती हैं की चालक के अंदर वैघृत क्षेत्र शून्य होता हैं तथा चालक के बाहर वैघृत क्षेत्र E होता हैं। अतः औसत वैघृत क्षेत्र `E/2` होगा जो प्लेटों की गतिशीलता के लिए उत्तरदायी हैं।