I धारावाही, N फेरों ओर R त्रिज्या वाली वृत्ताकार कुण्डली के लिए, इसके अक्ष पर, केंद्र से x दुरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र के लिए निम्न व्यंजक हैं-
$B = \frac{μ_{0} I R^{2} N}{2 {(x^{2} + R^{2})}^{3 / 2}}$
(a) स्पष्ट कीजिये, इसमें कुण्डली के केंद्र पर चुंबकीय क्षेत्र के लिए सुपरिचित परिणाम कैसे प्राप्त किया जा सकता हैं?
(b) बराबर त्रिज्या R एवं फेरों की संख्या N, वाली दो वृत्ताकार कुण्डलियाँ एक-दूसरे से R दुरी पर एक-दूसरे के समान्तर अक्ष मिला कर राखी गयी हैं। दोनों में समान विघुत धारा एक ही दिशा में प्रवाहित हो रही हैं। दर्शाइए की कुंडलियों के अक्ष के लगभग मध्य बिंदु पर क्षेत्र, एक बहुत छोटी दुरी के लिए जोकि R से कम हैं, एकसमान हैं ओर इस क्षेत्र का लगभग मान निम्न हैं-
$B = 0.72 \frac{μ_{0} N I}{R}$
(बहुत छोटे-से क्षेत्र पर एकसमान चुंबकीय क्षेत्र उत्पन्न करने के लिए बनायी गई ऊपर व्यवस्था हेल्म्होल्ट्ज के नाम से जानी जाती हैं।)

Video Solution

Text Solution

Verified by Experts

(a) दिया है- केंद्र से x दुरी पर चुंबकीय क्षेत्र,
$B = \frac{μ_{0} N I R^{2}}{2 {(x^{2} + R^{2})}^{3 / 2}}$
कुंडली के केंद्र पर चुंबकीय क्षेत्र प्राप्त करने हेतु $x = 0$ रखने पर,
$∴$ केंद्र पर चुंबकीय क्षेत्र $B = \frac{μ_{0} I R^{2} N}{2 R^{3}}$
$B = \frac{μ_{0} I N}{2 R}$
यह परिणाम धरा लूप के केंद्र पर चुंबकीय क्षेत्र के समान है।
(b) दोनों समान की अक्षीय कुंडलियों की त्रिज्या =R
तार के फेरों की संख्या =N
माना O कुंडलियों के बीच का मध्य बिंदु के समीवर्ती बिंदु है। माना
$O P = d (d < < R)$

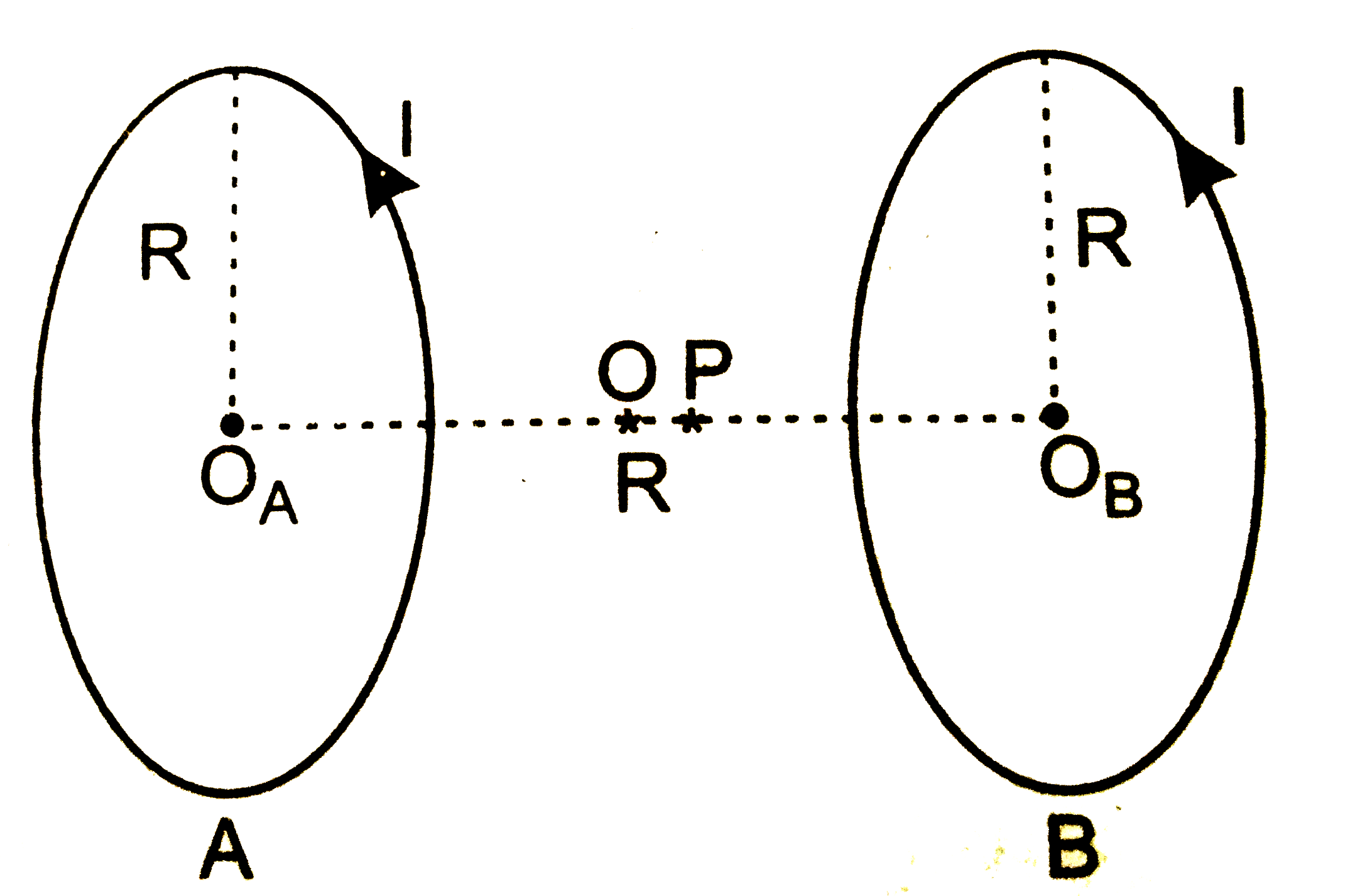
कुंडली A के लिए, $O_{A} P = \frac{R}{2} + d$
कुंडली A के कारण बिंदु P पर चुंबकीय क्षेत्र,
$B_{A} = \frac{μ_{0}}{4 π} . \frac{2 π n I R^{2}}{{(O_{A} P^{2} + R^{2})}_{A}^{3 / 2}}$
$= \frac{μ_{0}}{2} . \frac{N I . R^{2}}{{{(\frac{R}{2} + d)}^{2} + R^{2}}^{3 / 2}} = \frac{μ_{0} N I R^{2}}{{(2 [\frac{R^{2}}{4} + d^{2} + R d + R^{2}])}^{3 / 2}}$
प्रश्नानुसार, $d < < 2$ , अतः $d^{2}$ नगण्य है।
$B_{A} = \frac{μ_{0} N I R^{2}}{{(2 [\frac{5 R^{2}}{4} + R d])}^{3 / 2}} = \frac{μ_{0} N I R^{2}}{2 \times {(\frac{5 R^{2}}{4})}^{3 / 2}} = \frac{μ_{0} N I R^{2}}{2 \times {(\frac{5 R^{2}}{4})}^{3 / 2} {[1 \times \frac{R \times d \times 4}{5 R^{2}}]}^{3 / 2}}$
$= \frac{μ_{0} N I R^{2} {(1 + \frac{4 d}{5 R})}^{- 3 / 2}}{2 \frac{5 R^{2}}{{(4)}^{3 / 2}}}$ ...........(i)
मैक्सवेल के दाएं हाथ के नियमानुसार, $B_{A}$ की दिशा $P O_{B}$ के अनुदिश है
$B_{B} = \frac{μ_{0}}{4 π} . \frac{2 π N I R^{2}}{{(O_{B} P^{2} + R)}_{B}^{3 / 2}} = \frac{μ_{0}}{2} . \frac{2 N I R^{2}}{{[{(\frac{R}{2} - d)}^{2} + R^{2}]}^{3 / 2}}$
$\frac{μ_{0} N I R^{2}}{{(2 [\frac{R^{2}}{4} + d^{2} - R d + R^{2}])}^{3 / 2}}$
$= \frac{μ_{0} n I R^{2} {(1 - \frac{4 d}{5 R})}^{- 3 / 2}}{2 {[\frac{5 R^{2}}{4}]}^{3 / 22}}$ ( $d^{2}$ नगण्य लेने पर )
वैघृत क्षेत्र $B_{B}$ की दिशा $P O_{B}$ के अनुदिश है। अतः कुंडली A व B के कारण बिंदु P पर चुंबकीय क्षेत्र का परिमाण,
$B = B_{A} + B_{B} = \frac{μ_{0} . N I R^{2}}{2 {(\frac{5 R^{2}}{4})}^{3 / 2} [{(1 + \frac{4 d}{5 R})}^{- 3 / 2} + {(1 - \frac{4 d}{5 R})}^{- 3 / 2}]}$
द्विपद प्रमेय के प्रयोग द्वारा उछत्तम घातीय पदों
$B_{B} = \frac{μ_{0}}{4 π} . \frac{2 π N I R^{2}}{{(O_{B} P^{2} + R^{2})}_{B}^{3 / 2}} = \frac{μ_{0}}{2} . {⎡ ⎢ ⎢ ⎢ ⎣ \frac{2 N I R^{2}}{{(\frac{R}{2} - d)}^{2} + R^{2}} ⎤ ⎥ ⎥ ⎥ ⎦}^{3 / 2}$
$= \frac{μ_{0} N I R^{2}}{2 {[\frac{R^{2}}{4} + d^{2} - R d + R^{2}]}^{3 / 2}}$
$= \frac{μ_{0} n I R^{2} {(1 - \frac{4 d}{5 R})}^{- 3 / 2}}{2 {[\frac{5 R^{2}}{4}]}^{3 / 2}}$ ( $d^{2}$ नगण्य लेने पर)
वैघृत क्षेत्र $B_{B}$ की दिशा $P O_{B}$ के अनुदिश है। अतः कुंडली A or B के कारण बिंदु P पर चुंबकीय क्षेत्र का परिमाण,
$B = B_{A} + B_{B} = \frac{μ_{0} . N I R^{2}}{{(2 \frac{5 R^{2}}{4})}^{3 / 2}} [{(1 + \frac{4 d}{5 R})}^{- 3 / 2} + {(1 - \frac{4 d}{5 R})}^{- 3 / 2}]$
द्विपद प्रमेय के प्रयोग द्वारा उच्चतम घातिया पदों (जैसे $- d < < R$ ) को नगण्य मानते हुए, अब
$B = (μ_{0}) N I \frac{R^{2}}{{(2 \frac{5 R^{2}}{4})}^{3 / 2}} [1 - \frac{3}{2} \times \frac{4 d}{5 R} + 1 + \frac{3}{2} \times \frac{4 d}{5 R}]$
$B = \frac{μ_{0} N I R^{2}}{{(2 \frac{5 R^{2}}{4})}^{3 / 2}} [1 - \frac{3}{2} \times \frac{4 d}{5 R} + 1 \times \frac{3}{2} \times \frac{4 d}{5 R}]$
$= \frac{μ_{0} N I R^{2} 4^{3 / 2}}{2 \times R^{3} \times 5^{3 / 2}} \times 2 = \frac{μ_{0} N I}{2 R} {(\frac{4}{5})}^{3 / 2} \times 2$
$= {(\frac{4}{5})}^{3 / 2} . \frac{μ_{0} N I 2}{2 R} = \frac{2 μ_{0} N I}{2 R} = \frac{2 μ_{0} N I}{{(5)}^{3 / 2} 2 R} {(4)}^{3 / 2}$
$= 0.72 . \frac{μ_{0} N I}{R}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-गतिमान आवेश और चुंबकत्व -NCERT पाठय-पुस्तक के हल

Home
Ask Doubt
Profile