दिया गया है कि an=∫sin2{(n+1)x}sin2xdx
I. अनुक्रम {a2n}, सर्वान्तर शून्य के साथ AP में है।
II. अनुक्रम {a2n+1}, सर्वान्तर शून्य के साथ AP में है ।
उपरोक्त कथनों में से कौन -सा /से कथन सही है /हैं ?
केवल I
केवल II
I और II दोनों
न तो I और न ही II
The correct Answer is:C
∵a2n=∫π0sin2{(2n+1)x}sin2xdx...(i)
∫π0f(x)dx=∫π0f(π−x)dx के प्रगुण से,
a2n=∫π0sin2{(2n+1)(π−x)}sin2(π−x)dx
=∫π0sin2{(2n+1)x}−sin2xdx . . . (ii)
[∵n के किसी मान के लिए,
sin2{(2n+1)(π−x)}=sin2{(2n+1)x}
समी (i) और (ii) को जोड़ने पर,
2a2n=∫π0sin2{(2n+1)x}sin2xdx
⇒2a2n=0
∴a2n=0
उसी प्रकार, a2n+1=0 होगा|
अतः अनुक्रम {a2n}, सर्वान्तर शून्य के साथ समान्तर माध्य (AP) में है तथा अनुक्रम {a2n+1}, सर्वान्तर शून्य के साथ समान्तर माध्य (AP) में है ।
Topper's Solved these Questions
- निश्चित समाकलन BOOK - NDA PATHFINDERCHAPTER - निश्चित समाकलन EXERCISE - अभ्यास प्रश्नवाली
28 Videos
- द्विपद प्रमेय BOOK - NDA PATHFINDERCHAPTER - द्विपद प्रमेय EXERCISE - अभ्यास प्रश्नावली
50 Videos
- प्रतिलोम त्रिकोणमितीय फलक BOOK - NDA PATHFINDERCHAPTER - प्रतिलोम त्रिकोणमितीय फलक EXERCISE - अभ्यास प्रश्नावली (विगत वर्षों के प्रश्न )
18 Videos
Similar Questions
∫2π0sin2θa−bcosθdθ का मान है
View Solution(x2−2x)10 के प्रसार में x16 का गुणांक है
View Solutioncos{cos−1(45)+cos−1(1213)} का मान क्या है ?
View Solutionअभिक्रिया अनुक्रम में,
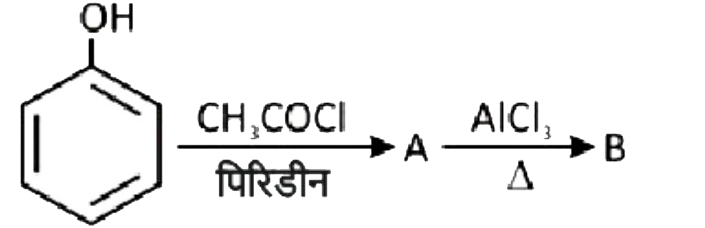
B के संबंध में सही कथन है:
View Solution
अभिक्रियाओं के उपरोक्त अनुक्रम में, Z है
View Solutionनिम्नलिखित कथनों में से कौन सा सही है?
View Solutionनिम्नलिखित में से कौन से जीनॉन के फ्लोराइड में शून्य द्विध्रुव आघूर्ण है?
View Solutionकृत्रिम मधुरकों के उपयोग के संबंध में निम्नलिखित में से कौन सा कथन सही है?
View Solutionशून्य कोटि अभिक्रिया के बारे में निम्नलिखित में से कौन सा कथन सत्य नहीं है?
View Solutionप्रकाश रासायनिक धूम के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solutionकार्बोनिल समूह के विषय में निम्नलिखित में से कौन सा कथन सही है?
View Solutionनिर्जल ऐलुमिनियम क्लोराइड के बारे में निम्नलिखित में से कौन सा कथन सही है ?
View Solutionनिम्नलिखित में से इलेक्ट्रानरागी के संबंध में कौन सा कथन सही है :
View Solutionदिए गए कथनों में से कौन सा कथन गलत है?
View Solutionएल्किल हैलाइडो के सम्बन्ध में निम्नलिखित में से कौन सा कथन सही है?
View Solutionषट्कोणीय निविड संकुलन के संबंध में निम्नलिखित में से कौन सा कथन सही नहीं है?
View Solution
