[A]: In paracentric inversions the centromere is outside the inverted segment.
[R]: In pericentric inversion, the inverted seg- ment includes the centromere
If both A and R are true and R is the correct explanation of A
If both A and R are true but R is not the correct explanation of A
If A is true and R is false
If both A and R are false
The correct Answer is:B
To solve the question regarding the assertion and reason about paracentric and pericentric inversions, we can follow these steps:
Step 1: Understand the Definitions
- Paracentric Inversion: This type of inversion occurs when the inverted segment does not include the centromere. Thus, the centromere remains outside the inverted segment.
- Pericentric Inversion: In this type of inversion, the inverted segment includes the centromere, meaning the centromere is part of the inverted segment.
Step 2: Analyze the Assertion
- The assertion states: "In paracentric inversions the centromere is outside the inverted segment."
- This statement is true because, by definition, paracentric inversions do not involve the centromere.
Step 3: Analyze the Reason
- The reason states: "In pericentric inversion, the inverted segment includes the centromere."
- This statement is also true as pericentric inversions are defined by the inclusion of the centromere in the inverted segment.
Step 4: Determine the Relationship Between Assertion and Reason
- While both the assertion and reason are true, the reason does not explain the assertion. The assertion is focused on paracentric inversion, while the reason discusses pericentric inversion, which is a different concept.
Step 5: Choose the Correct Option
- Based on the analysis, the correct option is: Both assertion and reason are true, but the reason is not the correct explanation of the assertion.
Final Answer
The correct answer is Option 2: Both assertion and reason are true, but reason is not the correct explanation of assertion.
---
- Paracentric Inversion: This type of inversion occurs when the inverted segment does not include the centromere. Thus, the centromere remains outside the inverted segment.
- Pericentric Inversion: In this type of inversion, the inverted segment includes the centromere, meaning the centromere is part of the inverted segment.
- The assertion states: "In paracentric inversions the centromere is outside the inverted segment."
- This statement is true because, by definition, paracentric inversions do not involve the centromere.
- The reason states: "In pericentric inversion, the inverted segment includes the centromere."
- This statement is also true as pericentric inversions are defined by the inclusion of the centromere in the inverted segment.
- While both the assertion and reason are true, the reason does not explain the assertion. The assertion is focused on paracentric inversion, while the reason discusses pericentric inversion, which is a different concept.
- Based on the analysis, the correct option is: Both assertion and reason are true, but the reason is not the correct explanation of the assertion.
The correct answer is Option 2: Both assertion and reason are true, but reason is not the correct explanation of assertion.
Topper's Solved these Questions
Similar Questions
Inversion without involving the centromere is called
View SolutionThe inverse of an invertible symmetric matrix is a symmetric matrix.
View SolutionDefine a binary operation * on the set A={0,1,2,3,4,5} as a⋅b=a+b (mod 6). Show that zero is the identity for this operation and each element a of the set is invertible with 6−a being the inverse of a. OR A binary operation * on the set {0,1,2,3,4,5} is defined as a⋅b={a+b,ifa+b<6a+b−6,ifa+b≥6 Show that zero is the identity for this operation and each element a of set is invertible with 6−a, being the inverse of a.
View SolutionDefine a binary operation * on the set A={0,1,2,3,4,5} as a⋅b=a+b (mod 6). Show that zero is the identity for this operation and each element a of the set is invertible with 6−a being the inverse of a. OR A binary operation * on the set {0,1,2,3,4,5} is defined as a⋅b={a+b,ifa+b<6a+b−6,ifa+b≥6 Show that zero is the identity for this operation and each element a of set is invertible with 6−a, being the inverse of a.
View SolutionDefine a binary operation ∗ on the set {0,1,2,3,4,5} as a∗b={a+bifa+b<6; a+b−6,ifa+b≥6. Show that zero is the identity for this operation and each element a≠0of the set is invertible with 6−a being the inverse of a
View SolutionNucleophilic aliphatic substitution reaction is mainly of two types: SN1 and SN2. The SN1 mechanism is a two step process. Reaction velocity of SN1 reaction depends only on the concentration of the substrate. Since product formation takes place by the formation of carbocation, optically active substrate gives (+) and (-) forms of the product. In most of the cases the product usually consits of 5−20% inverted product and 80−95% racemised species. The more stable the carbocation, the greater is the proportion of racemisation. In solvolysis reaction, the more nucleophilic the solvent, the greater is the proportion of inversion.
For the gives reaction,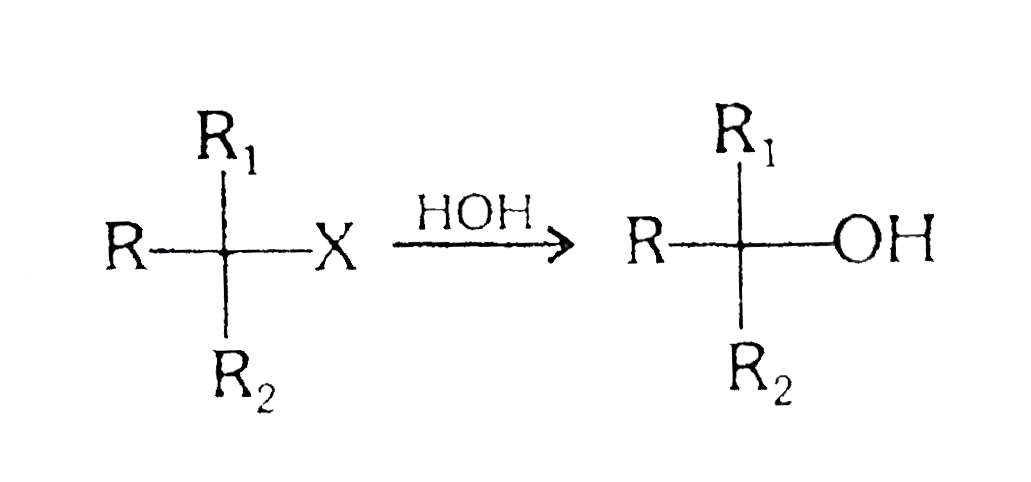
Which substrate will give maximum racemisation?
View SolutionNucleophilic aliphatic substitution reaction is mainly of two types: SN1 and SN2. The SN1 mechanism is a two step process. Reaction velocity of SN1 reaction depends only on the concentration of the substrate. Since product formation takes place by the formation of carbocation, optically active substrate gives (+) and (-) forms of the product. In most of the cases the product usually consits of 5−20% inverted product and 80−95% racemised species. The more stable the carbocation, the greater is the proportion of racemisation. In solvolysis reaction, the more nucleophilic the solvent, the greater is the proportion of inversion.
Which one of the following compound will give SN1 reaction predominantly?
View SolutionSN reaction is given by these compounds, which have a nuclophilic group and a good leaving EWG. It should be stable after leaving with bonding pair of ¯e's and it should have high polarisability.
Nucliphilic aliphatic substituion reaction is mainly of two types SN−1 and SN2.SN−1 mechanism is a two step process. Reaction velocity of SN−1 depends only on the concentration of the subtrate. It proceeds via the formation of carbocation, optically active substrate gives (⊕) and (o−) froms of the product.
In most of the cases, the product usually consists of 5−20% inverted and (95−80%) racemised species. The more stable is the carbocation, the greater is the propotion of racemission. In solvolysis reaction, the more nucleophillic is the solvent, the greater is the proportion of inversion.
Which of the following gives SN1 reaction?

Select the correct answer.
View SolutionTransformations of inverse trigonometric functions need to be handled with care. Consider the identity sin2θ=2tanθ1+tan2θ in its domain of definition. Suppose we set tanθ=x, we have sin2θ=2x1+x2
Taking sin−1of both sides yields 2θ=sin−1.2x1+x2i.e.,2tan−1x=sin−1.2x1+x2. But we will discover that the above identity is not valid for all x. Choose x=√3,LHS=2tan−1√3=2×π3=2π3,RHS=sin.2√31+3=sin−1.√32=π3. And so left hand and right hand side don't match. The reason is that we have disregarded the principal values of inverse functions. So it is well to remember that the iverse trigonometric formmulae have restrictions attached to the argument. When the values of x lie outside the interval of validity then the formula needs to be corrected.
Let f(x)=sin−1(x)1+x2,g(x)=2tan−1x. Then the largest interval in R on which f and g both are agree
View SolutionA binary operation * on the set {0,1,2,3,4,5} is defined as: a*b={a+b,a+b−6\ \ \ \ if\ a+b<6\ \ \ if a+b≥6 Show that zero is the identity for this operation and each element a of the set is invertible with 6-a, being the inverse of a.
View Solution
