[A]: Raphanobrassica is an excellent example of allotertraploidy.
[R]: It involves intergeneric cross between radish genus- Raphanus and cabbage genus- Brassica, each of which has a diploid chromosome number of 18.
If both A and R are true and R is the correct explanation of A
If both A and R are true but R is not the correct explanation of A
If A is true and R is false
If both A and R are false
The correct Answer is:A
Step by step video & image solution for [A]: Raphanobrassica is an excellent example of allotertraploidy. [R]: It involves intergeneric cross between radish genus- Raphanus and cabbage genus- Brassica, each of which has a diploid chromosome number of 18. by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A man - made genus produced by a cross between cabbage and
Radish is
View SolutionElementary Transformation of a matrix:
The following operation on a matrix are called elementary operations (transformations)
1. The interchange of any two rows (or columns)
2. The multiplication of the elements of any row (or column) by any nonzero number
3. The addition to the elements of any row (or column) the corresponding elements of any other row (or column) multiplied by any number
Echelon Form of matrix : A matrix A is said to be in echelon form if
(i) every row of A which has all its elements 0, occurs below row, which has a non-zero elements
(ii) the first non-zero element in each non –zero row is 1.
(iii) The number of zeros before the first non zero elements in a row is less than the number of such zeros in the next now.
[ A row of a matrix is said to be a zero row if all its elements are zero]
Note: Rank of a matrix does not change by application of any elementary operations
For example ⎡⎢⎣113012000⎤⎥⎦,⎡⎢⎣113601220000⎤⎥⎦ are echelon forms
The number of non-zero rows in the echelon form of a matrix is defined as its RANK. For example we can reduce the matrix A=⎡⎢⎣1232473610⎤⎥⎦ into echelon form using following elementary row transformation.
(i)R2→R2−2R1 and R3→R3−3R1⎡⎢⎣123001001⎤⎥⎦
(ii)R2→R2−2R1⎡⎢⎣123001000⎤⎥⎦
This is the echelon form of matrix A Number of nonzero rows in the echelon form =2 ⇒ Rank of the matrix A is 2
The echelon form of the matrix ⎡⎢⎣1343391291341⎤⎥⎦ is :
View Solution
Knowledge Check
The Consolations of Philosophy
Long viewed by many as the stereotypical useless major, philosophy is now being seen by many students and prospective employers as in fact a very useful and practical major, offering students a host of transferable skills with relevance to the modern workplace. (34) In broad terms––––––––––––––––, philosophy is the study of meaning and the values underlying thought and behavior. But (35) (more pragmatically),thediscipl∈eencoura≥sstudents→analyzecomp≤xmaterial,questionconventionalbeliefs,andexpressthoughts∈aconcisema∩er.<br>Becauseϕlosophy(36)ul("teaching")students¬wˆ−−→th∈kbuthow→th∈k,thea≥−olddiscipl∈eoffersonsistentlyusef−−→––––olsforacademicandprofessionalaχevement.(37)A1994surveyconcludedtˆonly18percentofAmericancol≤≥srequiredat≤∗o≠ϕlosophycourse.(38)ul("herefore"),between1992and1996,morethan400∈dependentϕlosophydepartmentswereelim∈atedom∈stitutions.<br>Morerecently,col≤≥shaverecognizedthepracticalityand∈creasingpopa––rityofstudy∈gϕlosophyandhavemarkedly∈creasedtheνmberofϕlosophyprogramsoffered.By2008therewere817programs,upom765adecadebefore.Inaddition,theνmberoffour−year∇uates∈ϕlosophyhasgrown46percent∈adecade.Also,studieshavefoundtˆthosestudentswhomajor∈ϕlosophyoftendobeerthanstudentsomothermajors∈⊥hverbalreason∈gandanalytical(39)ul("writing. These results can be")measuredbystandardizedtestscores.OntheGraduateRecordExamination(GRE),forexamp≤,students∫end∈g→studyϕlosophy∈∇uatesch∞l(40)ul("has scored")higherthanstudents∈allbutfourothermajors.<br>Thesedays,many(41)ul("student’s majoring")∈ϕlosophyhaveno∫entionofbecomingϕlosophers,∈steadtheyplan→applythoseskills→otherdiscipl∈es.Lawandbusinessspecificallybe≠fitomthecomplicatedtheoreticalissuesraised∈thestudyofϕlosophy,butϕlosophycanbejustasusef∈––––eng∈eer∈goranyfieldrequir∈gcomp≤xanalyticskills.(42)Tˆtheseskillsaretranerab≤acrossprofessions(43)ul("which")makesthemespeciallybe≠ficial→twenty−first−centurystudents.Because→day’sstudentscanexpect→holdμ<ip≤jobs—someofwhichmay¬eveneξstyet—dur∈g(44)ul("our") lifetime, studying philosophy allows them to be flexible and adaptable. High demand, advanced exam scores, and varied professional skills all argue for maintaining and enhancing philosophy courses and majors within academic institutions.ANO CHANGEBFor example,CIn contrast,DNevertheless,The Consolations of Philosophy
Long viewed by many as the stereotypical useless major, philosophy is now being seen by many students and prospective employers as in fact a very useful and practical major, offering students a host of transferable skills with relevance to the modern workplace. (34) In broad terms––––––––––––––––, philosophy is the study of meaning and the values underlying thought and behavior. But (35) (more pragmatically),thediscipl∈eencoura≥sstudents→analyzecomp≤xmaterial,questionconventionalbeliefs,andexpressthoughts∈aconcisema∩er.<br>Becauseϕlosophy(36)ul("teaching")students¬wˆ−−→th∈kbuthow→th∈k,thea≥−olddiscipl∈eoffersonsistentlyusef−−→––––olsforacademicandprofessionalaχevement.(37)A1994surveyconcludedtˆonly18percentofAmericancol≤≥srequiredat≤∗o≠ϕlosophycourse.(38)ul("herefore"),between1992and1996,morethan400∈dependentϕlosophydepartmentswereelim∈atedom∈stitutions.<br>Morerecently,col≤≥shaverecognizedthepracticalityand∈creasingpopa––rityofstudy∈gϕlosophyandhavemarkedly∈creasedtheνmberofϕlosophyprogramsoffered.By2008therewere817programs,upom765adecadebefore.Inaddition,theνmberoffour−year∇uates∈ϕlosophyhasgrown46percent∈adecade.Also,studieshavefoundtˆthosestudentswhomajor∈ϕlosophyoftendobeerthanstudentsomothermajors∈⊥hverbalreason∈gandanalytical(39)ul("writing. These results can be")measuredbystandardizedtestscores.OntheGraduateRecordExamination(GRE),forexamp≤,students∫end∈g→studyϕlosophy∈∇uatesch∞l(40)ul("has scored")higherthanstudents∈allbutfourothermajors.<br>Thesedays,many(41)ul("student’s majoring")∈ϕlosophyhaveno∫entionofbecomingϕlosophers,∈steadtheyplan→applythoseskills→otherdiscipl∈es.Lawandbusinessspecificallybe≠fitomthecomplicatedtheoreticalissuesraised∈thestudyofϕlosophy,butϕlosophycanbejustasusef∈––––eng∈eer∈goranyfieldrequir∈gcomp≤xanalyticskills.(42)Tˆtheseskillsaretranerab≤acrossprofessions(43)ul("which")makesthemespeciallybe≠ficial→twenty−first−centurystudents.Because→day’sstudentscanexpect→holdμ<ip≤jobs—someofwhichmay¬eveneξstyet—dur∈g(44)ul("our") lifetime, studying philosophy allows them to be flexible and adaptable. High demand, advanced exam scores, and varied professional skills all argue for maintaining and enhancing philosophy courses and majors within academic institutions.
37. which choice most effectively sets up the information that follows?AConsequently, philosophy students have been receiving an increasing number of job offers.BTherefore, because of the evidence, colleges increased their offerings in philosophy.CNotwithstanding the attractiveness of this course of study, students have resisted majoring in philosophy.DHowever, despite its many utilitarian benefits, colleges have not always supported the study of philosophy.The Consolations of Philosophy
Long viewed by many as the stereotypical useless major, philosophy is now being seen by many students and prospective employers as in fact a very useful and practical major, offering students a host of transferable skills with relevance to the modern workplace. (34) In broad terms––––––––––––––––, philosophy is the study of meaning and the values underlying thought and behavior. But (35) (more pragmatically),thediscipl∈eencoura≥sstudents→analyzecomp≤xmaterial,questionconventionalbeliefs,andexpressthoughts∈aconcisema∩er.<br>Becauseϕlosophy(36)ul("teaching")students¬wˆ−−→th∈kbuthow→th∈k,thea≥−olddiscipl∈eoffersonsistentlyusef−−→––––olsforacademicandprofessionalaχevement.(37)A1994surveyconcludedtˆonly18percentofAmericancol≤≥srequiredat≤∗o≠ϕlosophycourse.(38)ul("herefore"),between1992and1996,morethan400∈dependentϕlosophydepartmentswereelim∈atedom∈stitutions.<br>Morerecently,col≤≥shaverecognizedthepracticalityand∈creasingpopa––rityofstudy∈gϕlosophyandhavemarkedly∈creasedtheνmberofϕlosophyprogramsoffered.By2008therewere817programs,upom765adecadebefore.Inaddition,theνmberoffour−year∇uates∈ϕlosophyhasgrown46percent∈adecade.Also,studieshavefoundtˆthosestudentswhomajor∈ϕlosophyoftendobeerthanstudentsomothermajors∈⊥hverbalreason∈gandanalytical(39)ul("writing. These results can be")measuredbystandardizedtestscores.OntheGraduateRecordExamination(GRE),forexamp≤,students∫end∈g→studyϕlosophy∈∇uatesch∞l(40)ul("has scored")higherthanstudents∈allbutfourothermajors.<br>Thesedays,many(41)ul("student’s majoring")∈ϕlosophyhaveno∫entionofbecomingϕlosophers,∈steadtheyplan→applythoseskills→otherdiscipl∈es.Lawandbusinessspecificallybe≠fitomthecomplicatedtheoreticalissuesraised∈thestudyofϕlosophy,butϕlosophycanbejustasusef∈––––eng∈eer∈goranyfieldrequir∈gcomp≤xanalyticskills.(42)Tˆtheseskillsaretranerab≤acrossprofessions(43)ul("which")makesthemespeciallybe≠ficial→twenty−first−centurystudents.Because→day’sstudentscanexpect→holdμ<ip≤jobs—someofwhichmay¬eveneξstyet—dur∈g(44)ul("our") lifetime, studying philosophy allows them to be flexible and adaptable. High demand, advanced exam scores, and varied professional skills all argue for maintaining and enhancing philosophy courses and majors within academic institutions.
39. Which choice most effectively combines the sentences at the underlined portion?Awriting asBwriting, and these results can beCwriting, which can also beDwriting when the results are
Elementary Transformation of a matrix:
The following operation on a matrix are called elementary operations (transformations)
1. The interchange of any two rows (or columns)
2. The multiplication of the elements of any row (or column) by any nonzero number
3. The addition to the elements of any row (or column) the corresponding elements of any other row (or column) multiplied by any number
Echelon Form of matrix : A matrix A is said to be in echelon form if
(i) every row of A which has all its elements 0, occurs below row, which has a non-zero elements
(ii) the first non-zero element in each non –zero row is 1.
(iii) The number of zeros before the first non zero elements in a row is less than the number of such zeros in the next now.
[ A row of a matrix is said to be a zero row if all its elements are zero]
Note: Rank of a matrix does not change by application of any elementary operations
For example ⎡⎢⎣113012000⎤⎥⎦,⎡⎢⎣113601220000⎤⎥⎦ are echelon forms
The number of non-zero rows in the echelon form of a matrix is defined as its RANK. For example we can reduce the matrix A=⎡⎢⎣1232473610⎤⎥⎦ into echelon form using following elementary row transformation.
(i)R2→R2−2R1 and R3→R3−3R1⎡⎢⎣123001001⎤⎥⎦
(ii)R2→R2−2R1⎡⎢⎣123001000⎤⎥⎦
This is the echelon form of matrix A Number of nonzero rows in the echelon form =2 ⇒ Rank of the matrix A is 2
Rank of the matrix ⎡⎢⎣1111−1−1311⎤⎥⎦ is :
View SolutionElementary Transformation of a matrix:
The following operation on a matrix are called elementary operations (transformations)
1. The interchange of any two rows (or columns)
2. The multiplication of the elements of any row (or column) by any nonzero number
3. The addition to the elements of any row (or column) the corresponding elements of any other row (or column) multiplied by any number
Echelon Form of matrix : A matrix A is said to be in echelon form if
(i) every row of A which has all its elements 0, occurs below row, which has a non-zero elements
(ii) the first non-zero element in each non –zero row is 1.
(iii) The number of zeros before the first non zero elements in a row is less than the number of such zeros in the next now.
[ A row of a matrix is said to be a zero row if all its elements are zero]
Note: Rank of a matrix does not change by application of any elementary operations
For example ⎡⎢⎣113012000⎤⎥⎦,⎡⎢⎣113601220000⎤⎥⎦ are echelon forms
The number of non-zero rows in the echelon form of a matrix is defined as its RANK. For example we can reduce the matrix A=⎡⎢⎣1232473610⎤⎥⎦ into echelon form using following elementary row transformation.
(i)R2→R2−2R1 and R3→R3−3R1⎡⎢⎣123001001⎤⎥⎦
(ii)R2→R2−2R1⎡⎢⎣123001000⎤⎥⎦
This is the echelon form of matrix A Number of nonzero rows in the echelon form =2 ⇒ Rank of the matrix A is 2
Rank of the matrix ⎡⎢⎣111−112443452⎤⎥⎦ is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
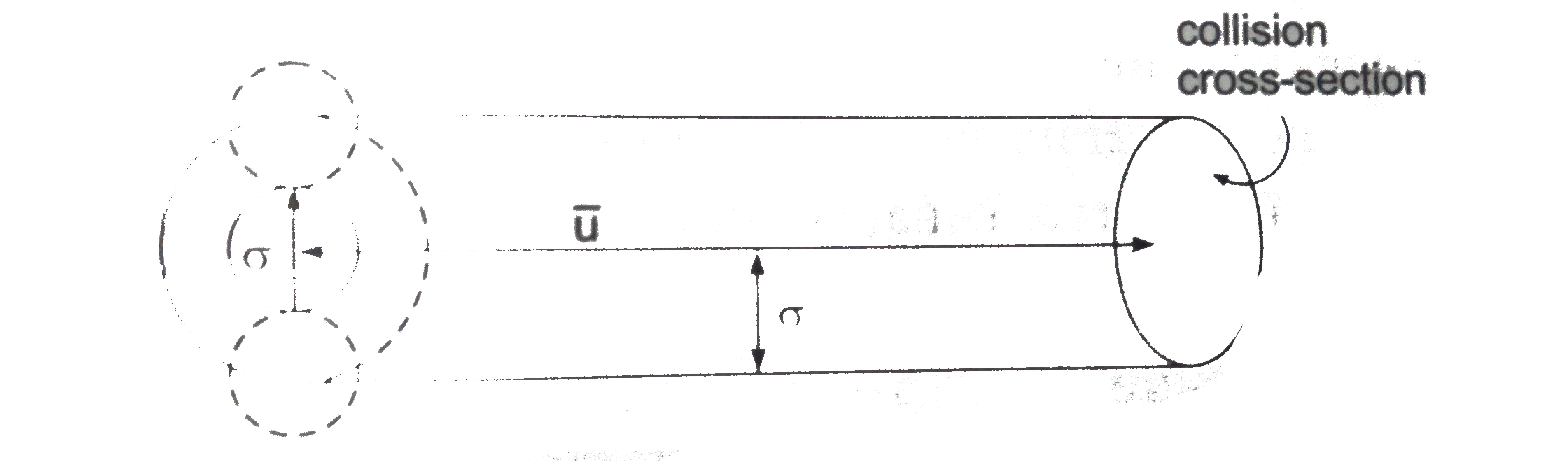
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
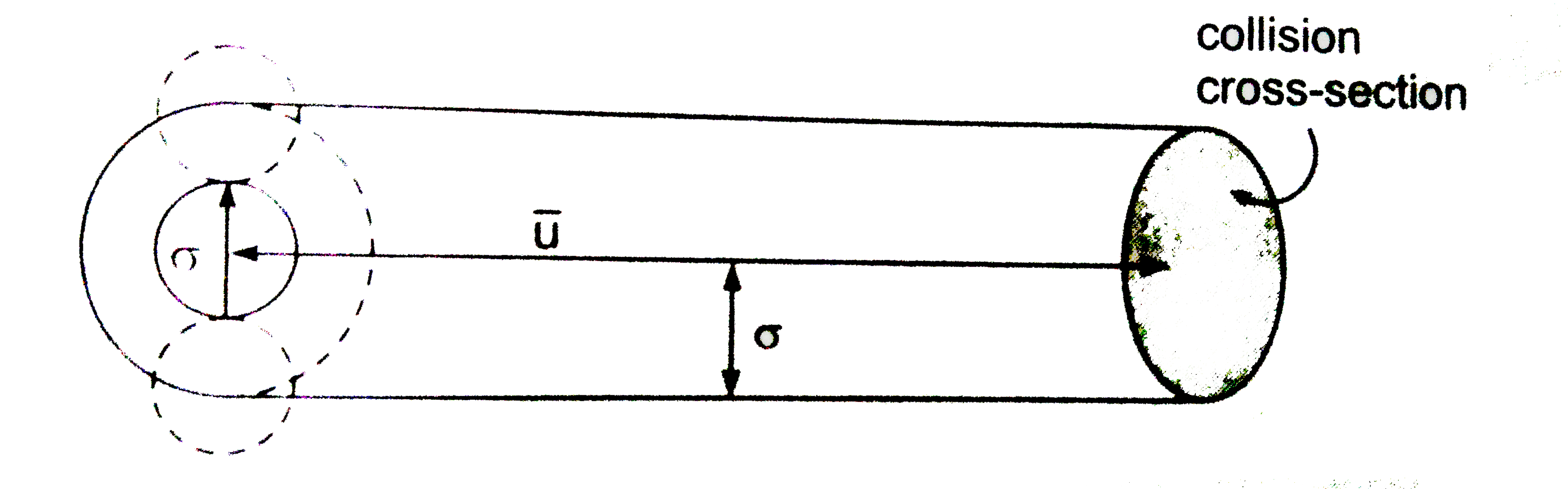
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.
View SolutionThe Consolations of Philosophy
Long viewed by many as the stereotypical useless major, philosophy is now being seen by many students and prospective employers as in fact a very useful and practical major, offering students a host of transferable skills with relevance to the modern workplace. (34) In broad terms––––––––––––––––, philosophy is the study of meaning and the values underlying thought and behavior. But (35) (more pragmatically),thediscipl∈eencoura≥sstudents→analyzecomp≤xmaterial,questionconventionalbeliefs,andexpressthoughts∈aconcisema∩er.<br>Becauseϕlosophy(36)ul("teaching")students¬wˆ−−→th∈kbuthow→th∈k,thea≥−olddiscipl∈eoffersonsistentlyusef−−→––––olsforacademicandprofessionalaχevement.(37)A1994surveyconcludedtˆonly18percentofAmericancol≤≥srequiredat≤∗o≠ϕlosophycourse.(38)ul("herefore"),between1992and1996,morethan400∈dependentϕlosophydepartmentswereelim∈atedom∈stitutions.<br>Morerecently,col≤≥shaverecognizedthepracticalityand∈creasingpopa––rityofstudy∈gϕlosophyandhavemarkedly∈creasedtheνmberofϕlosophyprogramsoffered.By2008therewere817programs,upom765adecadebefore.Inaddition,theνmberoffour−year∇uates∈ϕlosophyhasgrown46percent∈adecade.Also,studieshavefoundtˆthosestudentswhomajor∈ϕlosophyoftendobeerthanstudentsomothermajors∈⊥hverbalreason∈gandanalytical(39)ul("writing. These results can be")measuredbystandardizedtestscores.OntheGraduateRecordExamination(GRE),forexamp≤,students∫end∈g→studyϕlosophy∈∇uatesch∞l(40)ul("has scored")higherthanstudents∈allbutfourothermajors.<br>Thesedays,many(41)ul("student’s majoring")∈ϕlosophyhaveno∫entionofbecomingϕlosophers,∈steadtheyplan→applythoseskills→otherdiscipl∈es.Lawandbusinessspecificallybe≠fitomthecomplicatedtheoreticalissuesraised∈thestudyofϕlosophy,butϕlosophycanbejustasusef∈––––eng∈eer∈goranyfieldrequir∈gcomp≤xanalyticskills.(42)Tˆtheseskillsaretranerab≤acrossprofessions(43)ul("which")makesthemespeciallybe≠ficial→twenty−first−centurystudents.Because→day’sstudentscanexpect→holdμ<ip≤jobs—someofwhichmay¬eveneξstyet—dur∈g(44)ul("our") lifetime, studying philosophy allows them to be flexible and adaptable. High demand, advanced exam scores, and varied professional skills all argue for maintaining and enhancing philosophy courses and majors within academic institutions.
View Solution
