A tree grows at a rate of 0.5 m/yr . What will be the height of a board fixed at 1.5 m above the base, five years ago
4 m
3.5 m
1.5 m
4.5 m
The correct Answer is:c
To solve the problem, we need to determine the height of a board that was fixed at 1.5 meters above the base of a tree, considering the tree's growth over the past five years. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Growth Rate
The tree grows at a rate of 0.5 meters per year.
Step 2: Calculate Total Growth Over Five Years
To find out how much the tree has grown in five years, we multiply the growth rate by the number of years:
Total Growth=Growth Rate×Number of Years=0.5m/year×5years=2.5meters
Step 3: Determine the Height of the Tree Five Years Ago
If the tree has grown 2.5 meters over the last five years, we need to find out how tall the tree was five years ago. To do this, we subtract the total growth from the current height of the tree:
Height of Tree Five Years Ago=Current Height−Total Growth
Since the board is fixed at 1.5 meters above the base, we can assume that the height of the tree at that time was equal to the height of the board plus the growth:
Height of Tree Five Years Ago=1.5meters−2.5meters=−1.0meters
This indicates that the tree was not tall enough to reach the board five years ago.
Step 4: Find the Height of the Board Relative to the Tree's Growth
Since the board is fixed at 1.5 meters above the base, and the tree has grown to a height of 2.5 meters after five years, we can find the new position of the board relative to the tree:
New Height of the Board=Height of the Board+Total Growth=1.5meters+2.5meters=4.0meters
Step 5: Conclusion
The height of the board fixed at 1.5 meters above the base remains at 1.5 meters above the base of the tree, regardless of the tree's growth. Therefore, the height of the board five years ago would still be 1.5 meters above the base.
Final Answer
The height of the board fixed at 1.5 meters above the base, five years ago, is still 1.5 meters.
---
The tree grows at a rate of 0.5 meters per year.
To find out how much the tree has grown in five years, we multiply the growth rate by the number of years:
Total Growth=Growth Rate×Number of Years=0.5m/year×5years=2.5meters
If the tree has grown 2.5 meters over the last five years, we need to find out how tall the tree was five years ago. To do this, we subtract the total growth from the current height of the tree:
Height of Tree Five Years Ago=Current Height−Total Growth
Since the board is fixed at 1.5 meters above the base, we can assume that the height of the tree at that time was equal to the height of the board plus the growth:
Height of Tree Five Years Ago=1.5meters−2.5meters=−1.0meters
This indicates that the tree was not tall enough to reach the board five years ago.
Since the board is fixed at 1.5 meters above the base, and the tree has grown to a height of 2.5 meters after five years, we can find the new position of the board relative to the tree:
New Height of the Board=Height of the Board+Total Growth=1.5meters+2.5meters=4.0meters
The height of the board fixed at 1.5 meters above the base remains at 1.5 meters above the base of the tree, regardless of the tree's growth. Therefore, the height of the board five years ago would still be 1.5 meters above the base.
The height of the board fixed at 1.5 meters above the base, five years ago, is still 1.5 meters.
Topper's Solved these Questions
- BOOK - DINESH PUBLICATION ENGLISHCHAPTER - ANATOMY OF PLANT PARTSEXERCISE - CHECK YOUR GRASP10videos
ANATOMY OF PLANT PARTS
- BOOK - DINESH PUBLICATION ENGLISHCHAPTER - ANATOMY OF PLANT PARTSEXERCISE - BRAIN TEASERA -II35videos
ANATOMY OF PLANT PARTS
- BOOK - DINESH PUBLICATION ENGLISHCHAPTER - AMPHIBIA-VERTEBRATES WITH DUAL LIFE EXERCISE - check your grasp11videos
AMPHIBIA-VERTEBRATES WITH DUAL LIFE
- BOOK - DINESH PUBLICATION ENGLISHCHAPTER - ANIMAL TYPES EXERCISE - CHECK YOUR GRASP15videos
ANIMAL TYPES
Similar Questions
A tree is broken at a height of 5 m from the groundand its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree
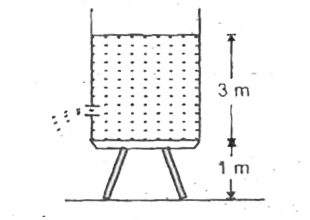
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A gardener is planting two types of trees. One type is seven feet tall and grows at a rate of 8 inches per year. The other type is four feet tall and its rate of the growth is 50% greater than the rate of the other tree. In how many years will the two grow to the same height?
A6B7C8D9
A boy of height 1.5m with his eye level at 1.4m stands before a plane mirror of length 0.75 m fixed on the wall. The height of the lower edge of the mirror above the floor is 0.8 m. Then ,
View SolutionA population grows at the rate of 5% per year. Then the population will be doubled in :
View SolutionThe radius of a right circular cylinder increases at the rate of 0.1 cm/min, and the height decreases at the rate of 0.2 cm/min. The rate of change of the volume of the cylinder, in cm2/m∈ , when the radius is 2cm and the height is 3cm is (a) −2π (b) −8π5 −3π5 (d) 2π5
View SolutionThe radius of a right circular cylinder increases at the rate of 0.1 cm/min, and the height decreases at the rate of 0.2 cm/min. The rate of change of the volume of the cylinder, in cm2/m∈ , when the radius is 2cm and the height is 3cm is (a) −2p (b) −8π5 −3π5 (d) 2π5
View SolutionA carpenter makes stools for electricians with a square top of side 0.5m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60∘ to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
View SolutionWater is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5m. How fast the water level is rising when the water stands 7.5 m below the base.
View SolutionWater is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5m. How fast the water level is rising when the water stands 7.5 m below the base.
View Solution

