Number of iron atoms present in haemoglobin molecule is
One
Two
Three
Four
The correct Answer is:D
To determine the number of iron atoms present in a hemoglobin molecule, we can follow these steps:
1. Understand the Structure of Hemoglobin: Hemoglobin is a protein found in red blood cells (RBCs) that is essential for transporting oxygen from the lungs to the tissues and carbon dioxide from the tissues back to the lungs.
2. Identify the Components of Hemoglobin: Hemoglobin is composed of four polypeptide chains, which consist of two types: two alpha (α) subunits and two beta (β) subunits.
3. Recognize the Role of Heme Groups: Each of the four polypeptide chains is associated with a heme group. The heme group is a complex that contains iron.
4. Determine the Iron Content: Each heme group contains one iron (Fe) atom. Since there are four heme groups (one for each polypeptide chain), we can conclude that there is one iron atom per heme group.
5. Calculate the Total Number of Iron Atoms: Since there are four heme groups in total, and each heme group contains one iron atom, the total number of iron atoms in a hemoglobin molecule is:
Total Iron Atoms=4 (one from each heme group)
6. Select the Correct Answer: Based on the calculation, the number of iron atoms present in a hemoglobin molecule is 4. Therefore, the correct answer is option D: 4.
Final Answer:
The number of iron atoms present in a hemoglobin molecule is 4.
---
Total Iron Atoms=4 (one from each heme group)
The number of iron atoms present in a hemoglobin molecule is 4.
Topper's Solved these Questions
- CELL CYCLE (CELL DIVISION)BOOK - DINESH PUBLICATION ENGLISHCHAPTER - CELL CYCLE (CELL DIVISION)EXERCISE - CHECK YOUR GRASP
18 Videos
- BIOLOGICAL CLASSIFICATION BOOK - DINESH PUBLICATION ENGLISHCHAPTER - BIOLOGICAL CLASSIFICATION EXERCISE - CYC
13 Videos
- CHEMICAL COORDINATION AND REGULATIONBOOK - DINESH PUBLICATION ENGLISHCHAPTER - CHEMICAL COORDINATION AND REGULATIONEXERCISE - Brain Teasers-V
114 Videos
Similar Questions
Knowledge Check
Assertion: Molecular formula shows the exact number of different types of atoms present in a molecule of a compound.
Reason : Molecular formula can be obtained directly from empirical formula which represents the simplest whole number ratio of various atoms present in a compound.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Subunits present in haemoglobin are:
View SolutionNumber of hetero atoms present in the given compound is :
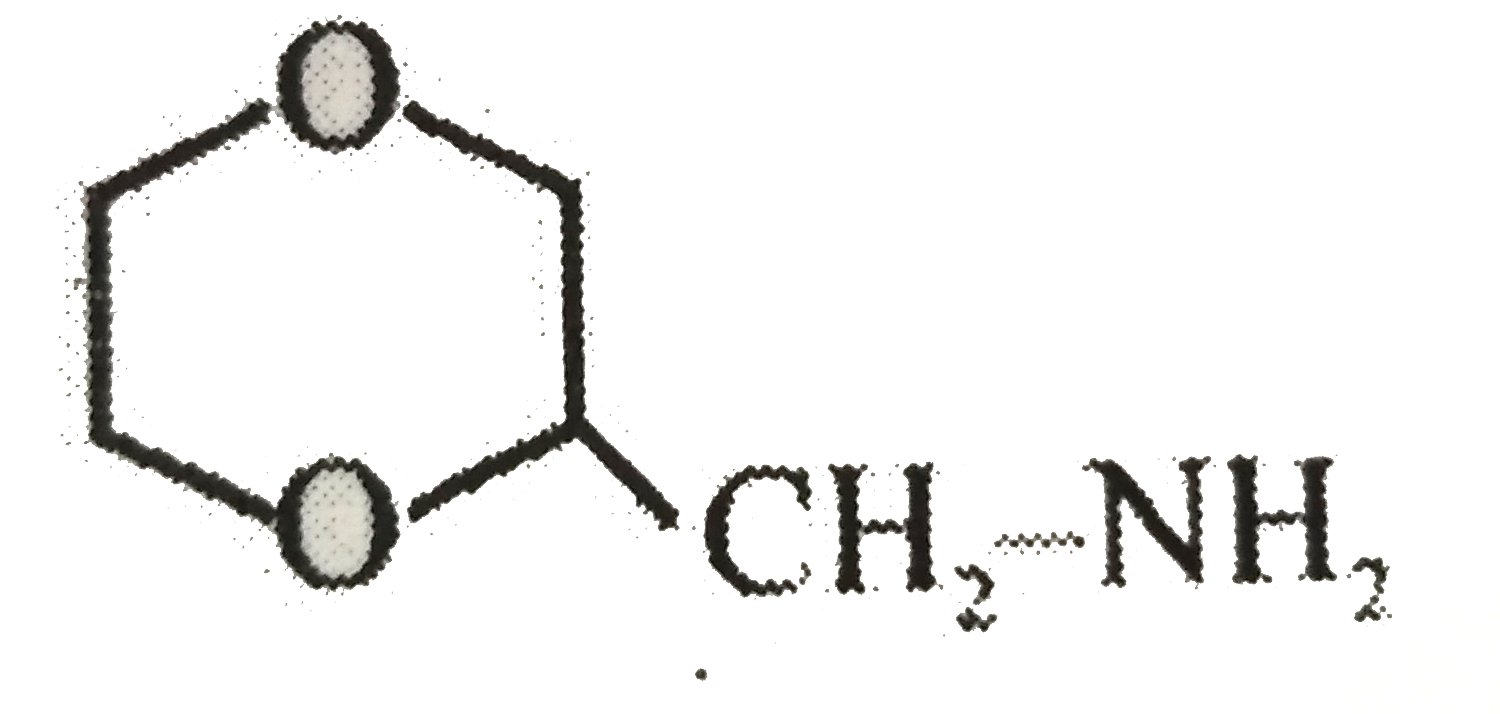
View SolutionTotal number of nitrogen atoms present in urotropine is :
View SolutionThe number of atoms present in one molecule of an element is called its______
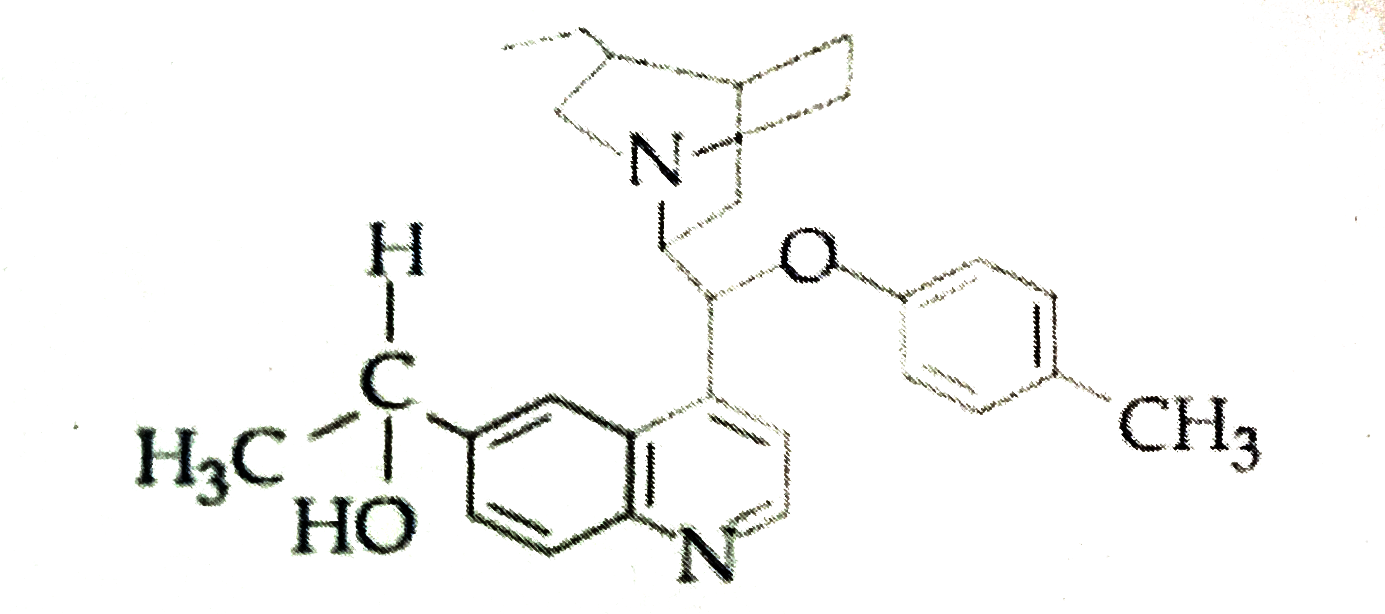
View SolutionThe number of chiral carbons present in he molecule given below is ______ .
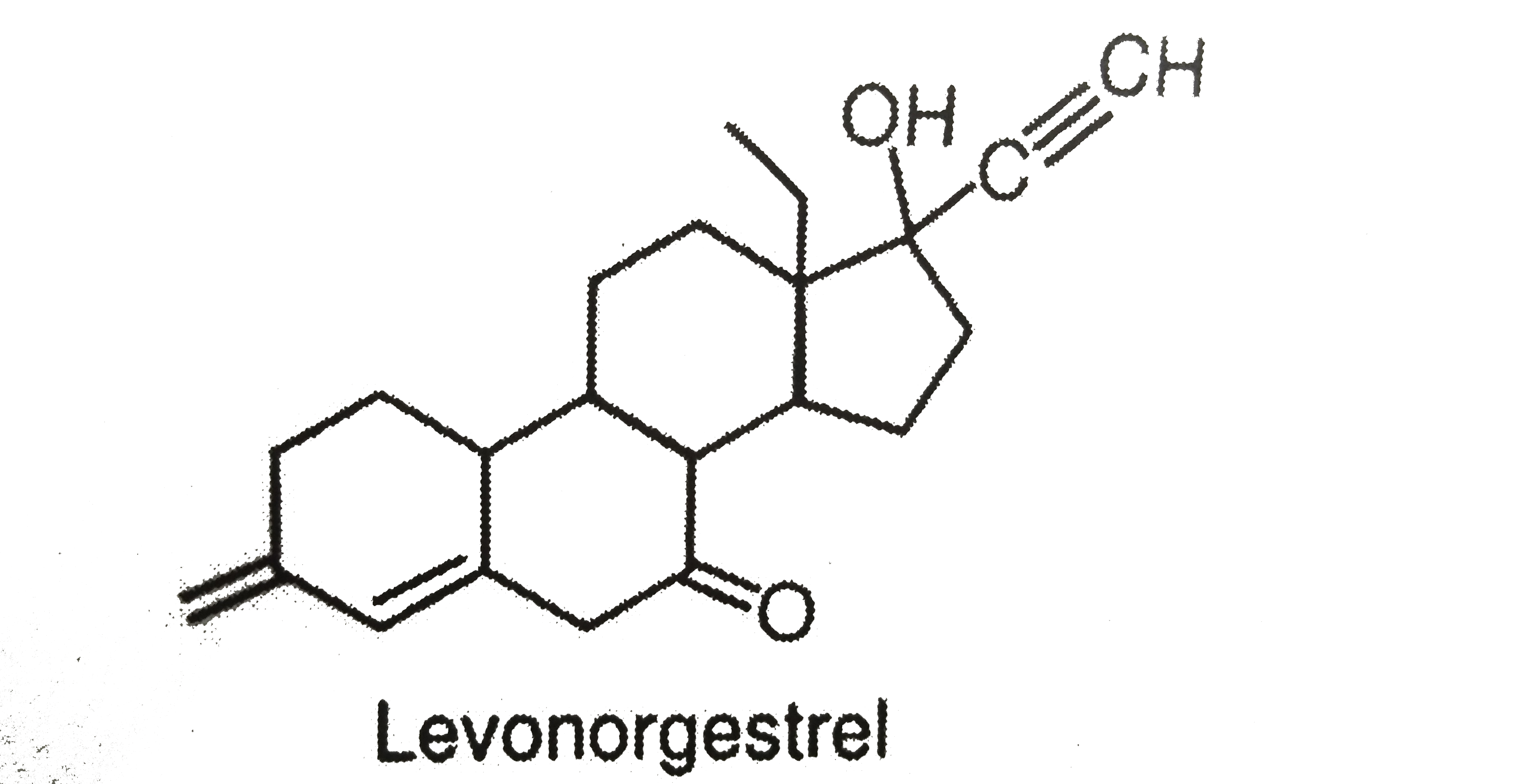
View SolutionLevonorgestrel is a commonly used contraceptive. The number of chiral centres present in this molecule is:
View SolutionName the polypeptides present in a haemoglobin molecule.
View Solution
