Organisms 'X' and 'Y' live in close association with each other. 'X' depends on 'Y' for support and 'Y' depends on 'X' for its food. Which of the following pairs represents organisms 'Xand 'Y"?
Cuscuta and Peepal tree
Pitcher plant and insect
Fungi and bacteria
Fungi and algae
To solve the question about organisms 'X' and 'Y' that live in close association, we need to analyze the relationships described:
1. Understanding the Relationship:
- Organism 'X' depends on 'Y' for support.
- Organism 'Y' depends on 'X' for food.
- This indicates a mutualistic symbiotic relationship where both organisms benefit from each other.
2. Identifying the Organisms:
- We need to look at the options provided:
1. Cascata and People Tree
2. Picture Plant and Insect
3. Fungi and Bacteria
4. Fungi and Algae
3. Analyzing Each Pair:
- Cascata and People Tree: This does not represent a mutualistic relationship where one provides support and the other provides food.
- Picture Plant and Insect: Picture plants trap insects for nutrients, but the relationship is not about support.
- Fungi and Bacteria: While they can have interactions, this pair does not fit the description provided.
- Fungi and Algae: In this relationship, algae (X) perform photosynthesis and produce food, which supports fungi (Y). In return, fungi provide support and nutrients to algae.
4. Conclusion:
- The correct pair representing organisms 'X' and 'Y' is Fungi and Algae. Algae (X) provides food for fungi (Y), and fungi provide support to algae.
Final Answer:
The pair representing organisms 'X' and 'Y' is Fungi and Algae.
- Organism 'X' depends on 'Y' for support.
- Organism 'Y' depends on 'X' for food.
- This indicates a mutualistic symbiotic relationship where both organisms benefit from each other.
- We need to look at the options provided:
1. Cascata and People Tree
2. Picture Plant and Insect
3. Fungi and Bacteria
4. Fungi and Algae
- Cascata and People Tree: This does not represent a mutualistic relationship where one provides support and the other provides food.
- Picture Plant and Insect: Picture plants trap insects for nutrients, but the relationship is not about support.
- Fungi and Bacteria: While they can have interactions, this pair does not fit the description provided.
- Fungi and Algae: In this relationship, algae (X) perform photosynthesis and produce food, which supports fungi (Y). In return, fungi provide support and nutrients to algae.
- The correct pair representing organisms 'X' and 'Y' is Fungi and Algae. Algae (X) provides food for fungi (Y), and fungi provide support to algae.
The pair representing organisms 'X' and 'Y' is Fungi and Algae.
Topper's Solved these Questions
- LIFE UNDER A MICROSCOPE ( MICROOGANISMS)BOOK - BETOPPERSCHAPTER - LIFE UNDER A MICROSCOPE ( MICROOGANISMS)EXERCISE - Summative Worksheet (Multiple Choice Question)
12 Videos
- LIFE UNDER A MICROSCOPE ( MICROOGANISMS)BOOK - BETOPPERSCHAPTER - LIFE UNDER A MICROSCOPE ( MICROOGANISMS)EXERCISE - Summative Worksheet (Fill in the blanks)
11 Videos
- LIFE UNDER A MICROSCOPE ( MICROOGANISMS)BOOK - BETOPPERSCHAPTER - LIFE UNDER A MICROSCOPE ( MICROOGANISMS)EXERCISE - Summative Worksheet (True or False)
8 Videos
- DIGESTIONBOOK - BETOPPERSCHAPTER - DIGESTIONEXERCISE - SUMMATIVE WORKSHEET
3 Videos
- MOVEMENT IN ANIMALS AND PLANTSBOOK - BETOPPERSCHAPTER - MOVEMENT IN ANIMALS AND PLANTSEXERCISE - SUMMATIVE WORKSHEET (ANSWER THE FOLLOWING )
13 Videos
Similar Questions
Knowledge Check
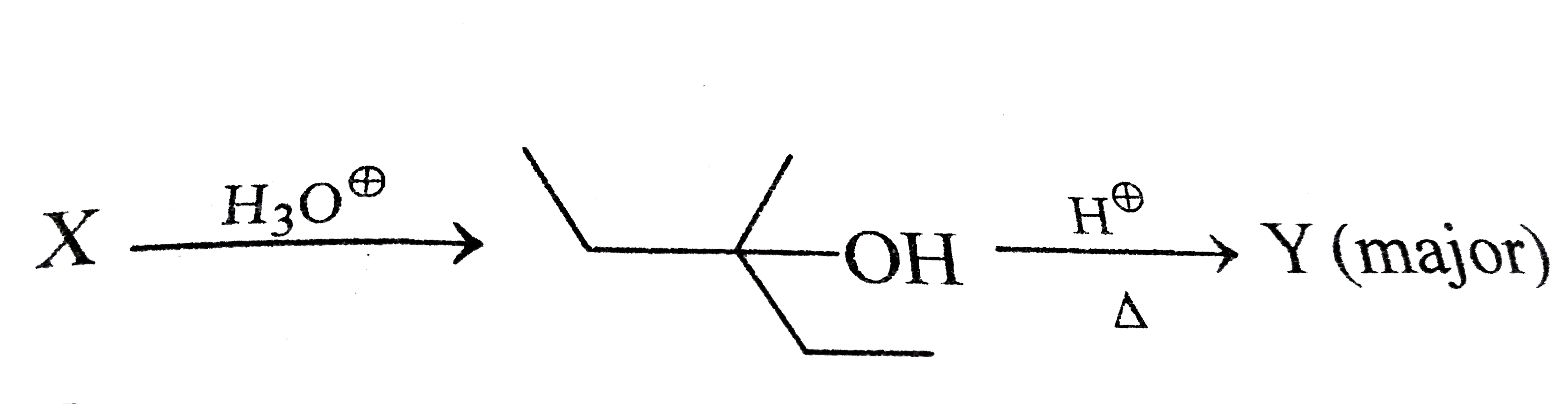
Y (major)
X & Y may relate with each other asAChain isomersBPosition isomersCGeometrical isomersDIdenticalIf y=f(x)andx=g(y) are inverse functions of each other, then
Ag''(y)=1f''(x)Bg''(y)=f''(x)(f''(x))3Cg''(y)=f'(x)(f'(x))3DNone of these
Factorize each of the following expressions : x(x+z)−y(y+z)
View SolutionConsumers are the organisms that cannot manufacture their own food and are dependent on other organisms for food. The illustration represents a food chain
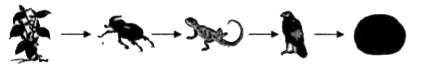
Which of the following pairs of organisms represents the consumers in the given food chain?
View SolutionBoth x and y vary directly with each other and when x is 10, y is 14, which of the following is not a possible pair of corresponding values of x and y?
View SolutionBoth x and y vary inversely with each other. When x is 10, y is 6, which of the following is not a possible pair of corresponding values of x and y?
View SolutionThe mode of nutrition in which an organism depends on other organism for their food is known as ______ .
View SolutionFind the derivative of y w.r.t. x in each of the following :
yx+y=3+x3.
View Solution
