The three boxes in this diagram represent the three major biosynthetic pathways in aerobic respiration. Arrows represent net reactants or products
Arrows numbered 4, 8 and 12 can all be

H2O
FAD+orFADH2
NADH
ATP
The correct Answer is:4
Pathway A represents Glycolysis , B is Kreb 's cycle and C is ETC
ATP is produced in all these three pathways (represented by 4,8,12)
NADH is produced in pathways A and B , not in C
FADH2 is produced only in pathway B
H2O is produced in A & C, not in Kreb's cycle
Topper's Solved these Questions
Similar Questions
Which intermediate product is found in all three of the following process
(a) anaerobic respiration
(b) aerobic respiration
(c) photosynthesis
View SolutionIn a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17
View Solution
Knowledge Check
The chart below shows the number of small and large packages of a certain brand of cereal that were bought over a three - day period. The proce of a small box of this brand is $ 2.99, and the price of a large box is $3.99. Which of the following matrix expression represents the income, in dollars, received from the sale of cereal each of the three days ?
Day 1Day 2Day 3Large758257Small433650A[758257433650][2.99 3.99]B⎡⎢⎣754382365750⎤⎥⎦[3.992.99]C[758257433650][2.993.99]D[2.993.99]⎡⎢⎣754382365750⎤⎥⎦To make its sales goals for the month, a toy manufacture must sell at least $10,400 for of toy hoops and basketballs. Toy hoops sell for $8 and basketballs sell for $25. The company hopes to sell more than three times as many basketballs as toy hoops. If h represents the number of toy hoops and b represents the number of basketballs, where h and b are positive integer, which of the following systemsof inequalities best describes this situation ?
A8h+25b≥10
400b>3hB8h+25b≥10
400>3bC25h+8b≥10
400b>3hD25h+8b≥10
400h>3bThe use of calculator is not permitted.
The Boulevard Hotel has a peculiar way of numbering its rooms. The first room on each floor is numbered as the product of all floor number below it starting from floor number on ( the ground floor is not counted). For example , the first room on the fourth floor would be numbered as 1×2×3=6. All successive room numbers would be numbered three more than the previous room number. Thus , on the fourth floor, rooms are numbered as 6,6+3=9,6+2×3=12,6+3×3=15 etc. If it is known that there are six rooms on each floor, how many numbers on the fifteenth floor are prime numbers ?A0B2C4D5
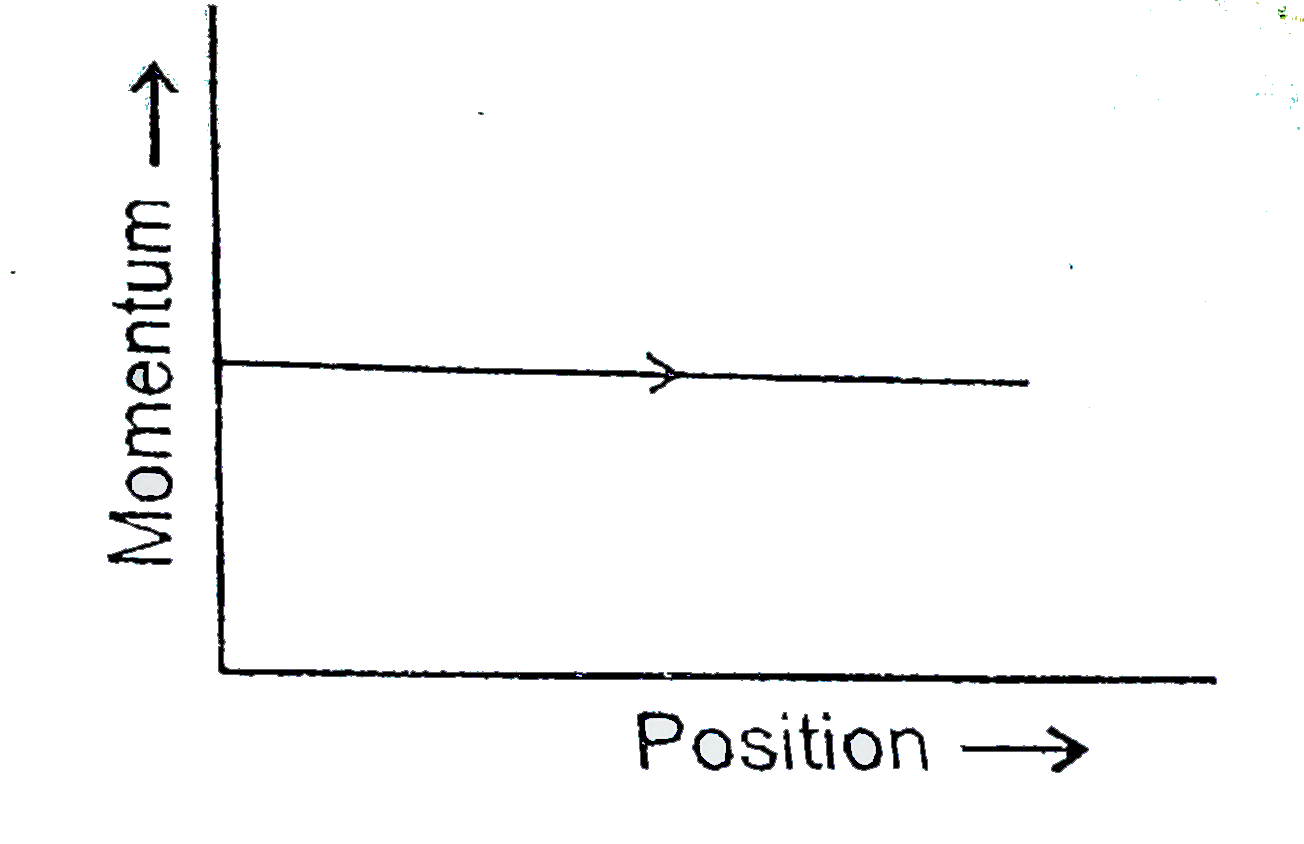
Phase space deagrams are useful tools
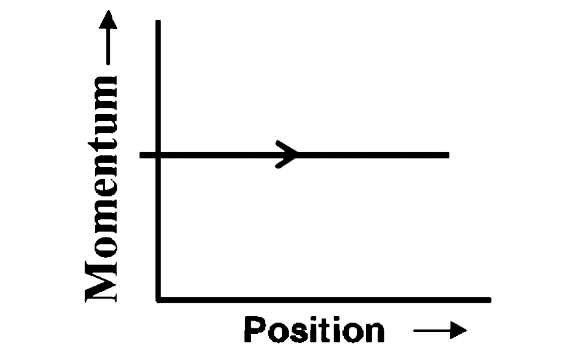 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
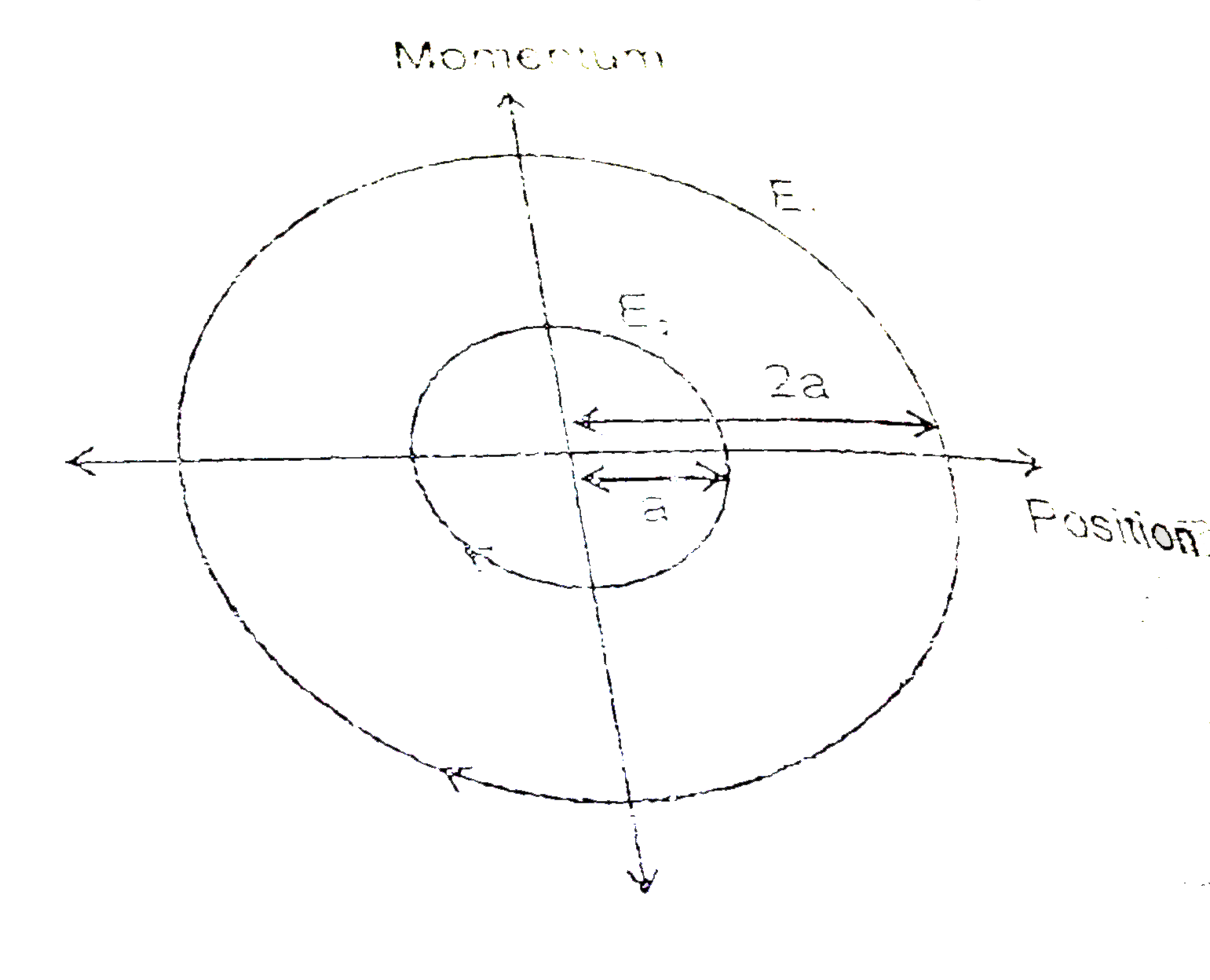
The plase space deagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial condetions, and E_(1) and E_(2) the total mechanical energies respectivey.
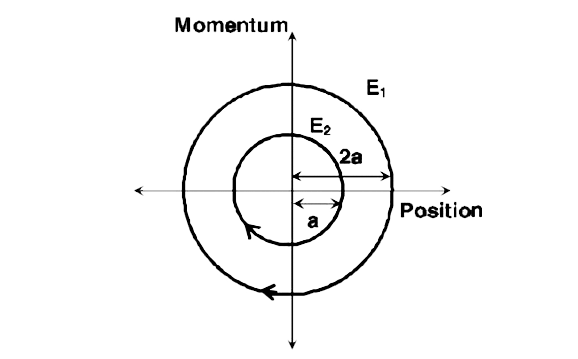 .
.
View Solutionfigure depicts a block sliding along a frictionless ramp in vertical plane Eight numbered arrows in the diagram repreesent direction to be referred to when answering the questions
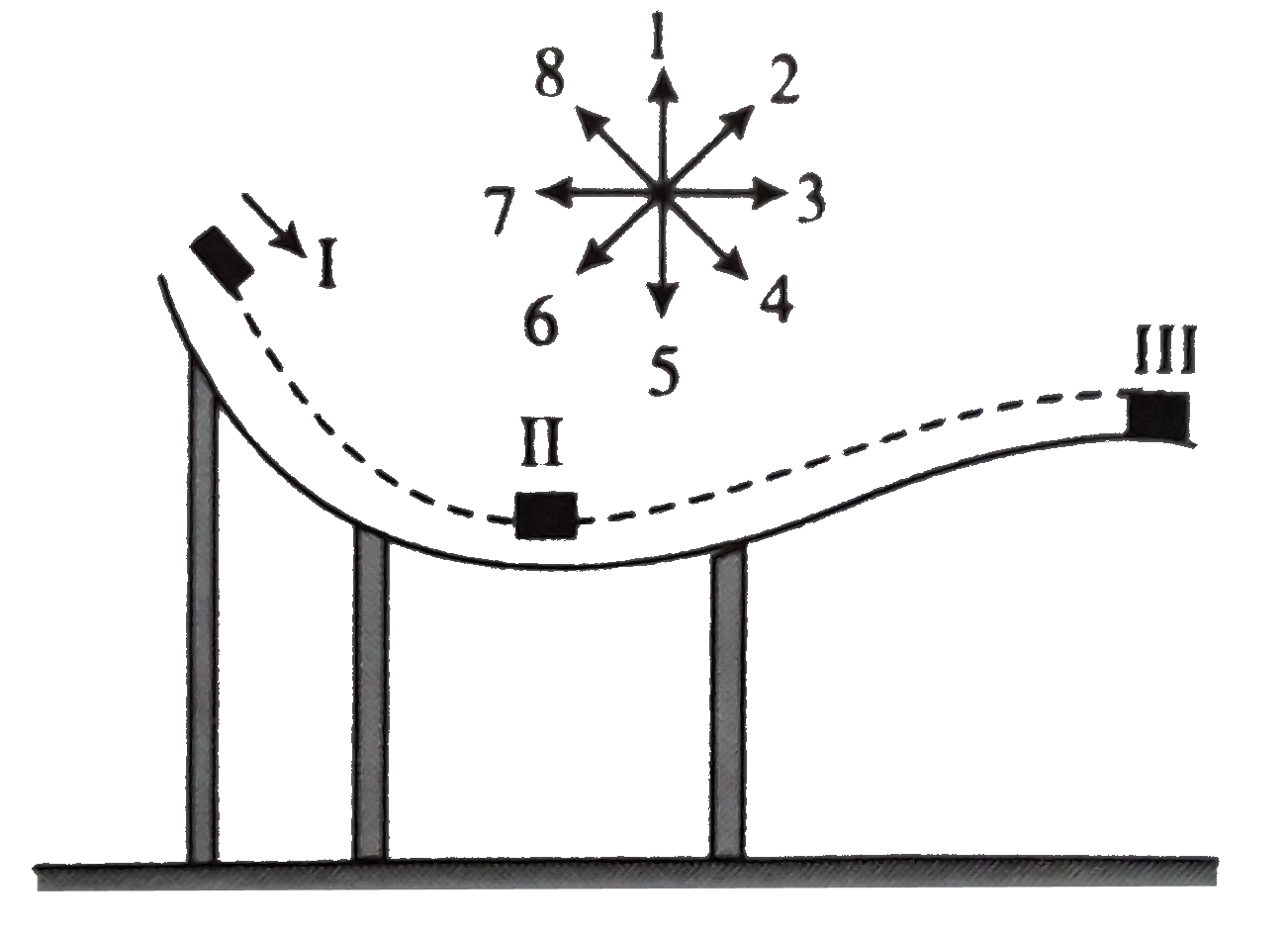
Position - i : Starts sliding on curve path
Position - ii : Lowest position of the curve path
Position - iii : Just outside of the curve path
The direction of the acceleration of the blocks (after leaving the ramp) at position i is best represented by which of the arrows in the diagram?
View Solutionfigure depicts a block sliding along a frictionless ramp in vertical plane Eight numbered arrows in the diagram repreesent direction to be referred to when answering the questions
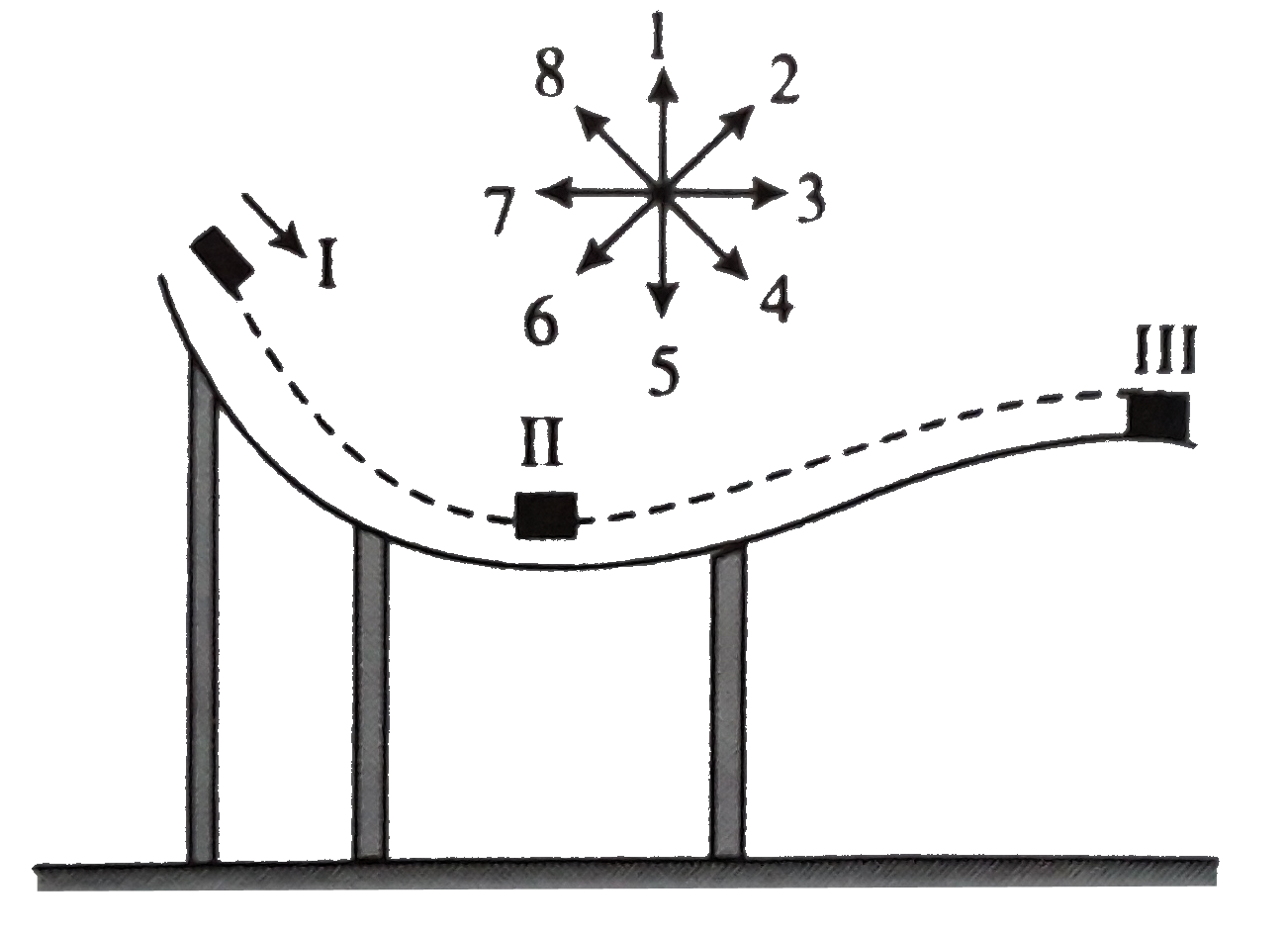
Position - i : Starts sliding on curve path
Position - ii : Lowest position of the curve path
Position - iii : Just outside of the curve path
The direction of the acceleration of the blocks when in position ii is best represented by which of the arrows in the diagram?
View SolutionPhase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.
The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
View SolutionName any three types of isomerism that the compound with molecular formula C4H7CI can give rise to. Also represent the structures of the compounds relevant to these isomers.∗∗
View Solution
