W1=W0 ert is the expression of exponential growth , in which r denotes .
Initial growth
Final growth
Relative growth rate
Base of natural logarithms
The correct Answer is:C
To solve the question regarding the expression of exponential growth W1=W0ert and what r denotes, we can break it down step by step.
1. Understanding the Equation: The equation W1=W0ert represents exponential growth, where:
- W1 is the final size (weight, height, number, etc.).
- W0 is the initial size.
Hint: Identify the components of the equation to understand their meanings.
2. Identifying the Base: In the equation, e is the base of the natural logarithm. This is a constant approximately equal to 2.71828.
Hint: Recall that e is a mathematical constant used in exponential functions.
3. Understanding r: The variable r in the equation represents the growth rate. It indicates how quickly the growth occurs over time.
Hint: Think about what growth rate means in the context of population or size changes.
4. Understanding t: The variable t represents time. It indicates the duration over which the growth occurs.
Hint: Consider how time influences growth in biological systems.
5. Final Interpretation: Since the question specifically asks what r denotes, we conclude that r represents the relative growth rate.
Hint: Look for options that align with the definition of growth rate in the context of the equation.
Conclusion:
The correct answer is that r denotes the relative growth rate.
- W1 is the final size (weight, height, number, etc.).
- W0 is the initial size.
The correct answer is that r denotes the relative growth rate.
Topper's Solved these Questions
- PLANT GROWTH AND DEVELOPMENT Book:AAKASH SERIESChapter:PLANT GROWTH AND DEVELOPMENT Exercise:EXERCISE - I (PLANT GROWTH REGULARTORS - GENERAL )
Explore 12 Videos
- PLANT GROWTH AND DEVELOPMENT Book:AAKASH SERIESChapter:PLANT GROWTH AND DEVELOPMENT Exercise:EXERCISE - I (AUXINS )
Explore 15 Videos
- PHOTOSYNTHESIS IN HIGHER PLANTS Book:AAKASH SERIESChapter:PHOTOSYNTHESIS IN HIGHER PLANTS Exercise:Exercise - III
Explore 27 Videos
- PRINCIPLES AND PROCESSES Book:AAKASH SERIESChapter:PRINCIPLES AND PROCESSES Exercise:Exercise - III (Previous AIPMT/NEET Questions)
Explore 26 Videos
Similar Questions
Knowledge Check
ΔU=q+w, is mathematical expression for
Afirst law of thermodynamicsBsecond law of thermodynamicsCthird law of thermodynamicsDzeroth law of thermodynamicsWhich of the following equations corretly represents the exponential population growth curve ?
AdN/dt=rNBdN/dt=rN(K−NK)CNt=N0ertDBoth (a) and (c)
In exponential growth formula, Wt=W0ert,e denotes
View SolutionSelect the incorrect statement w.r.t. growth.
View SolutionGo through the following statements
(i) In geometr,ic growth, following mitotic cell division, only one daughter cell con- tinues to divide while the other differen- tiates and mature.
(ii) The ability of plants to follow different pathways in response to environment or phases of life to to.rm different kinds of structures, is called plasticity.
(iii) The mathematical expression for arith- metic growth is Lt=L0+rt while for geo- metric growth, it is W1=W0=W0ert
(iv) The form of growth wherein new cells are always being added to the plant body by the activity of the meristem, is called the open form of growth.
Which of these are correct .
View SolutionTwo weights W1 and W2 in equilibrium and at rest, are suspended as shown in figure. Then the ratio W1W2 is :
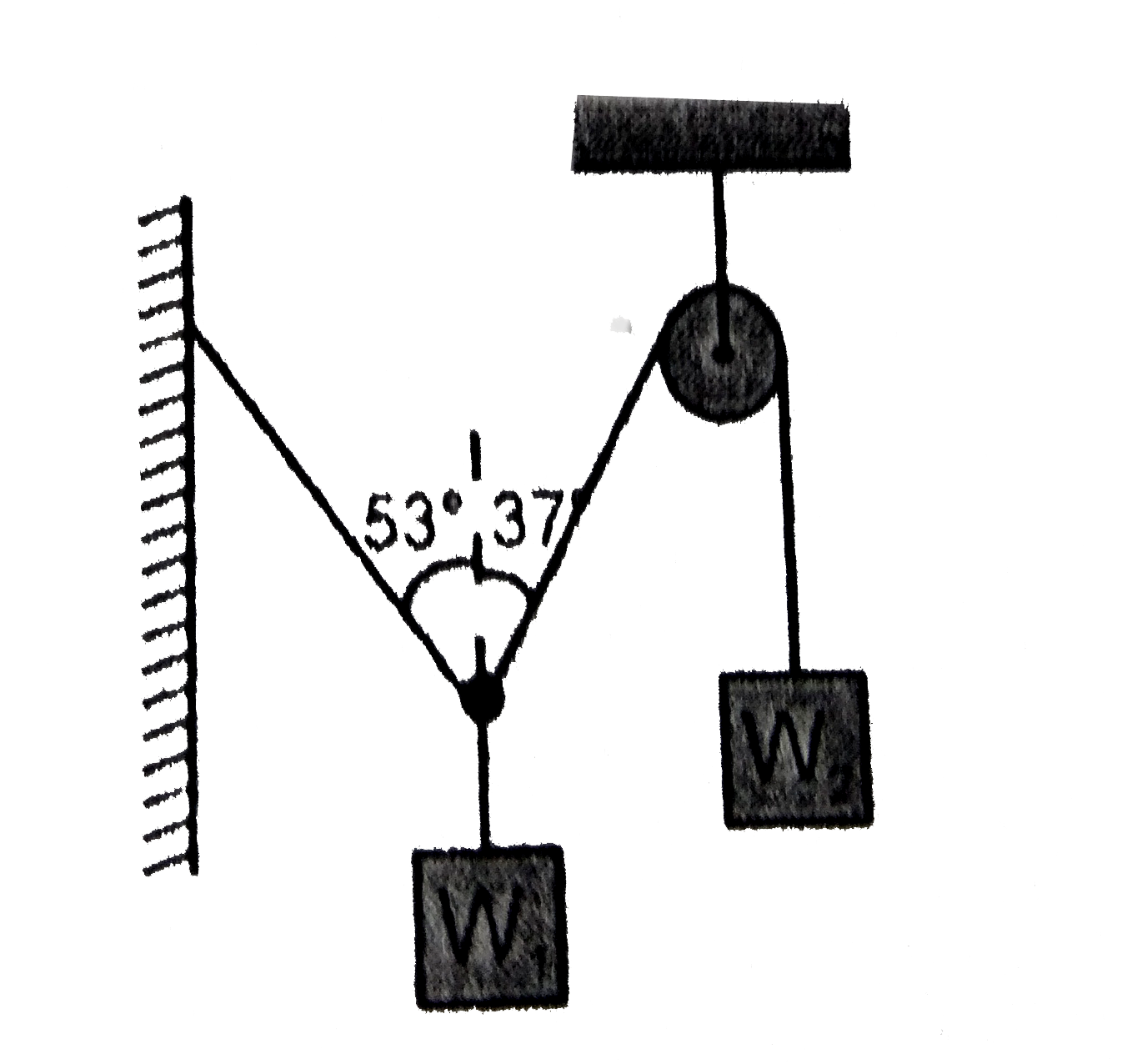
View SolutionIf R1 and R2 are the resistances of the filaments of 200 W and 100 W electric bulbs operated at 220 V, then (R1R2) is
View SolutionTwo potentiometer wires w1 and w2 of equal length l connected to a battery of emf εP and internal resistance 'r' as shown through two switches s1 and s2. A battery of emf ε is balanced on these potentiometer wires. if potentiometer wire w1 is of resistance 2r and balancing length on w1 is l/2 when only s1 is closed and s2 is open. On closing s2 and opening s1 the balancing length on w2 is found to be (2l3) then find the resistance of potentiometer wire w2
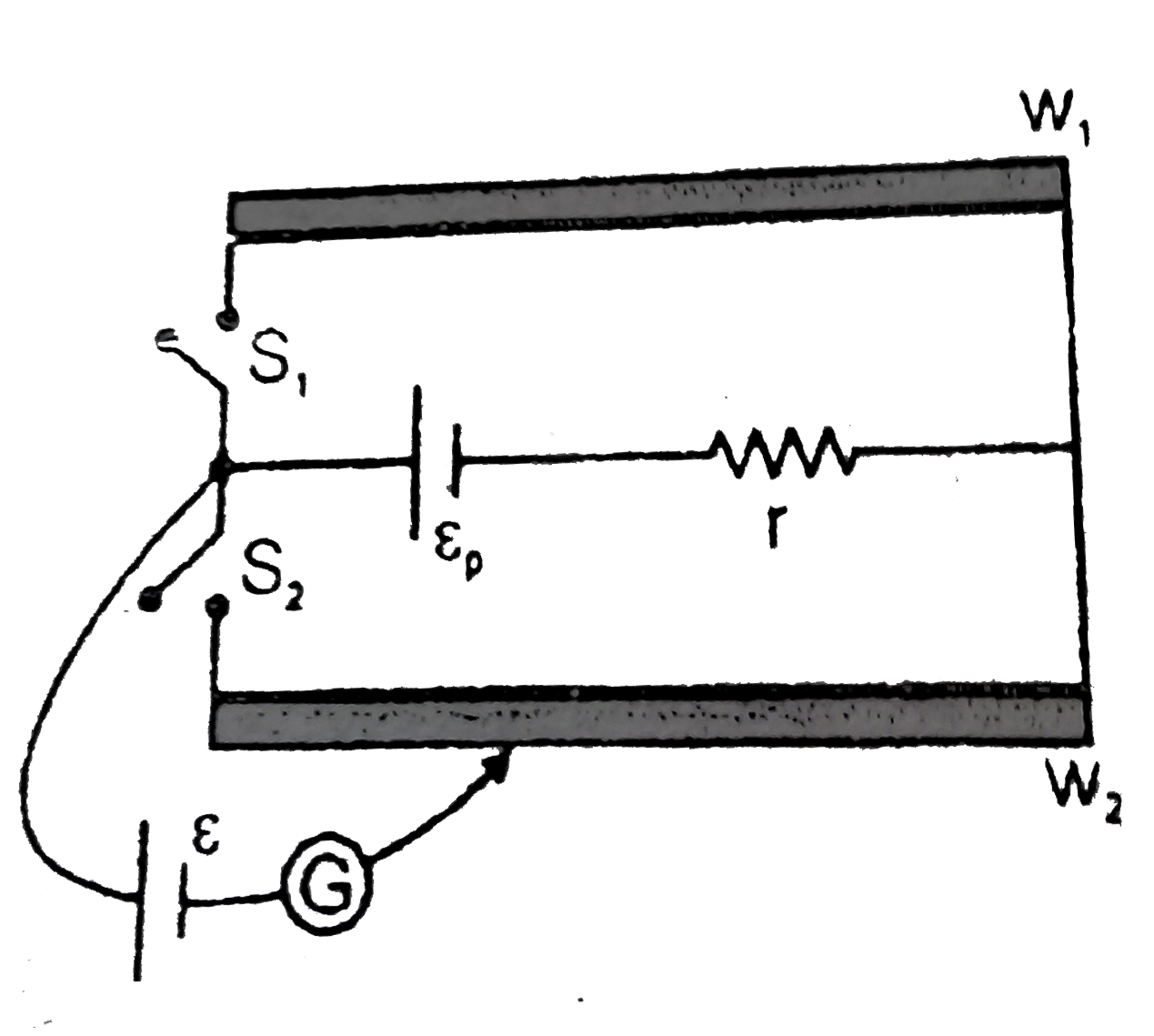
View Solution