(2R,3r)-2,3 bantanediol is :
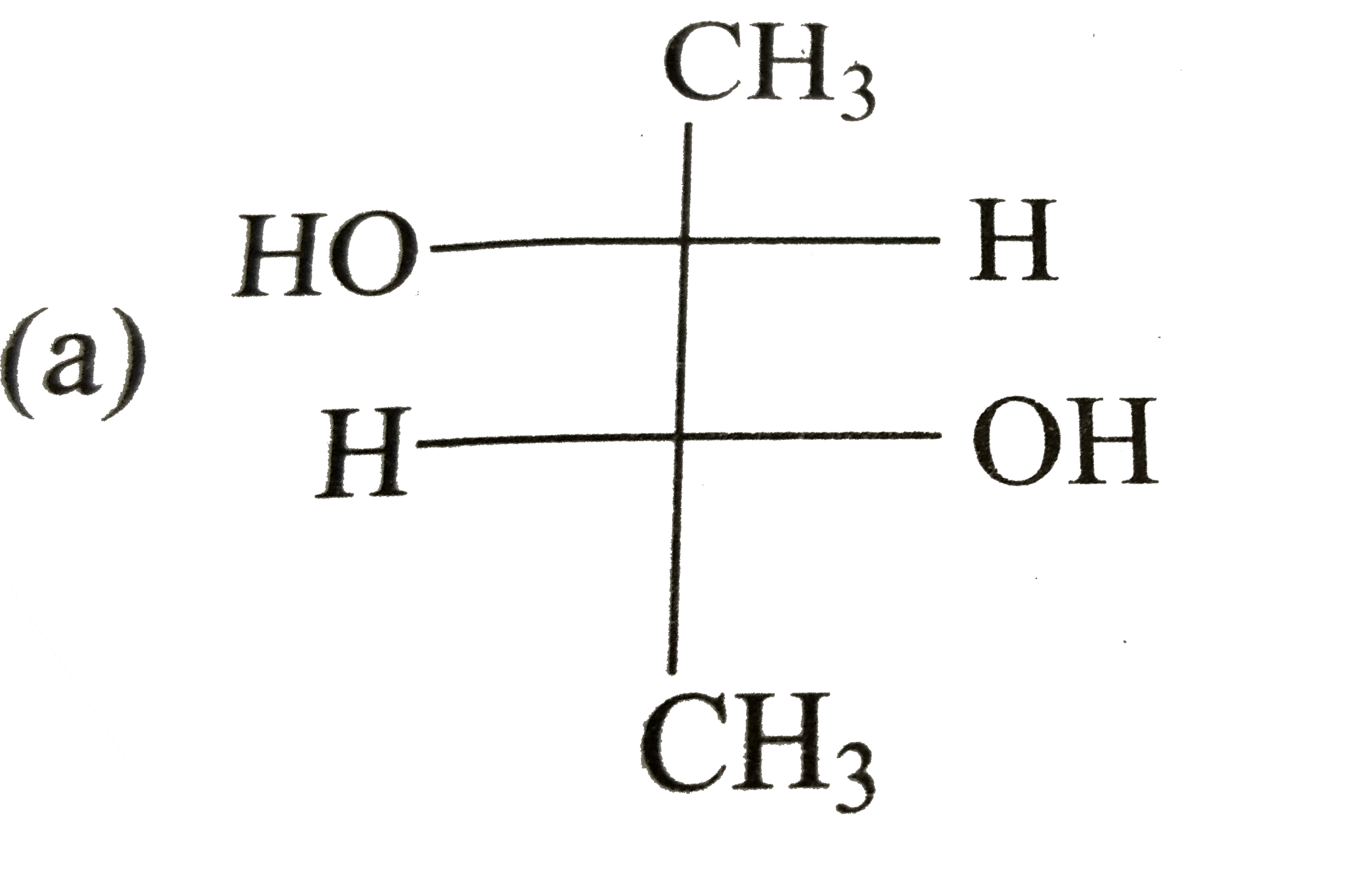

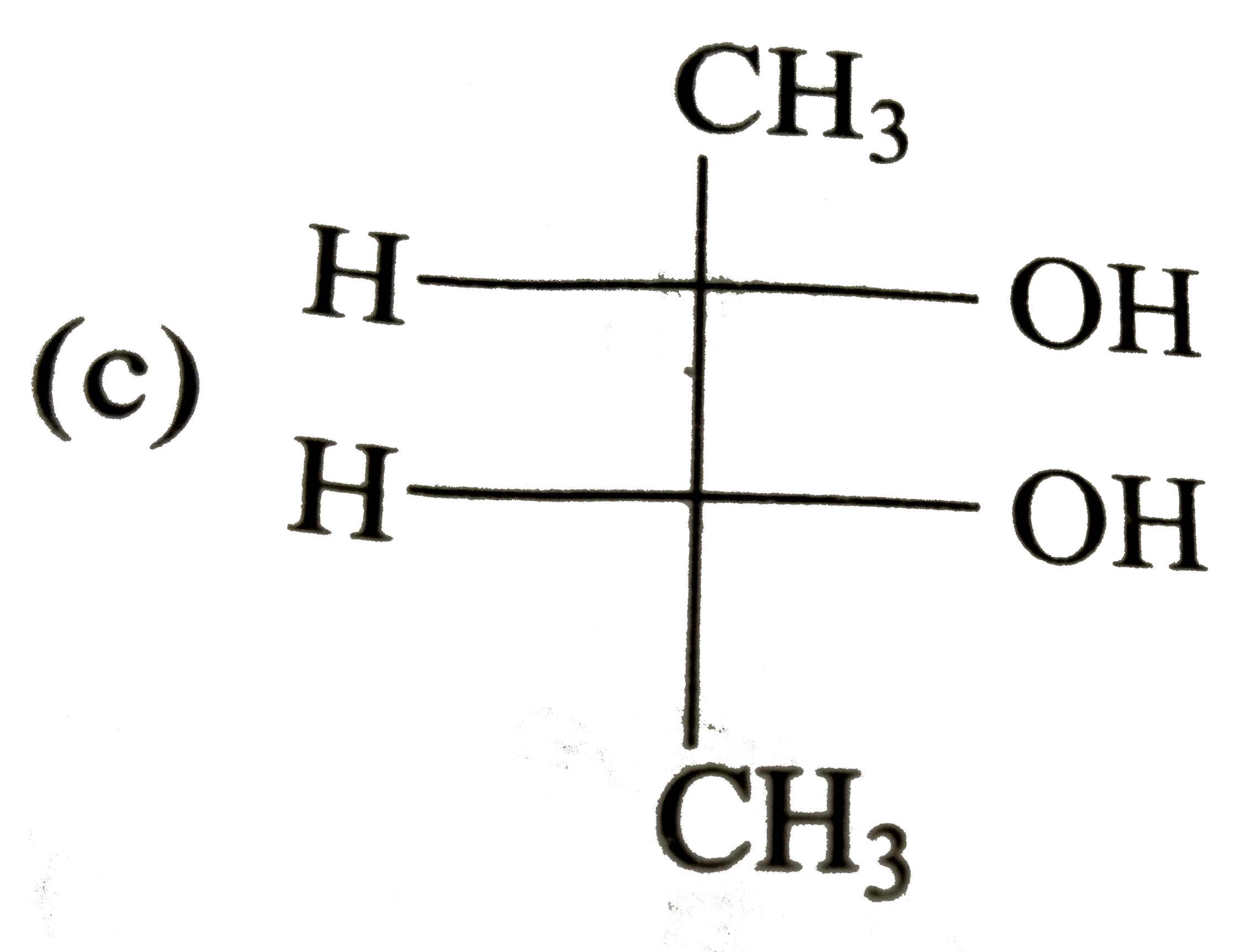
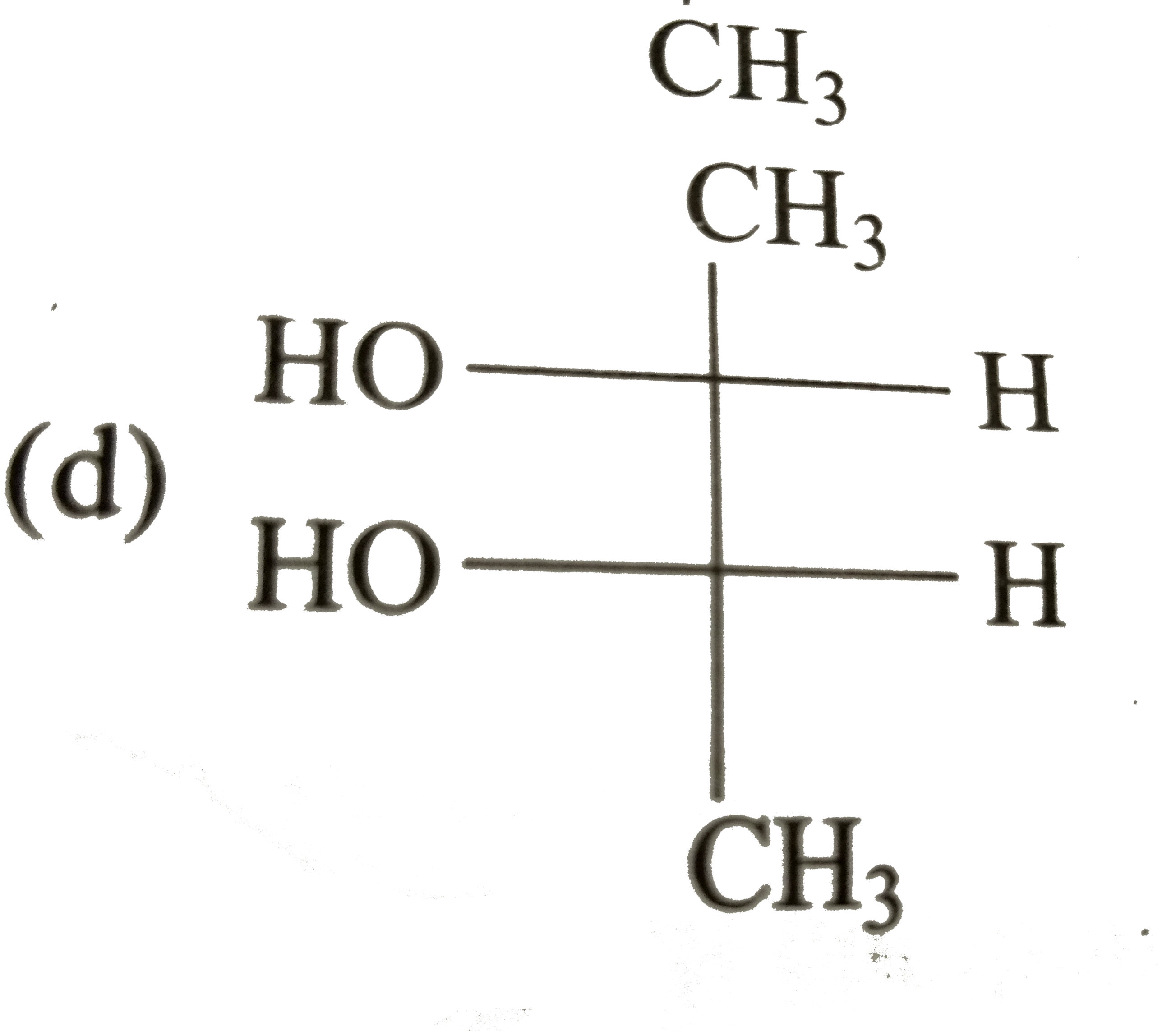
The correct Answer is:A
To determine the correct structure of (2R,3R)-2,3-butanediol, we need to analyze the stereochemistry of the compound based on the given R configurations at the 2nd and 3rd carbon atoms. Here’s a step-by-step breakdown of how to approach this problem:
Step 1: Understand the Structure of Butanediol
Butanediol has the formula C4H10O2 and consists of a four-carbon chain with hydroxyl (-OH) groups attached to the 2nd and 3rd carbon atoms. The structure can be represented as follows:
CH3−CH(OH)−CH(OH)−CH3
Step 2: Identify the Stereocenters
In (2R,3R)-2,3-butanediol, the stereocenters are at the 2nd and 3rd carbon atoms. Each of these carbons is attached to four different groups, which allows us to assign R or S configurations.
Step 3: Assign Priorities to the Groups
Using the Cahn-Ingold-Prelog priority rules, we assign priorities to the substituents attached to the stereocenters:
- For carbon 2:
- -OH (hydroxyl group) has the highest priority (1)
- -CH3 (methyl group) has the next priority (2)
- -CH2- (the carbon chain) has the next priority (3)
- The hydrogen atom (H) has the lowest priority (4)
- For carbon 3:
- -OH (hydroxyl group) has the highest priority (1)
- -CH3 (methyl group) has the next priority (2)
- -CH2- (the carbon chain) has the next priority (3)
- The hydrogen atom (H) has the lowest priority (4)
Step 4: Determine the Configuration
To determine the configuration (R or S), we look at the arrangement of the groups:
- For carbon 2, if we position the lowest priority group (H) at the back, the order of the remaining groups (1, 2, 3) is clockwise, which gives it an R configuration.
- For carbon 3, if we position the lowest priority group (H) at the back, the order of the remaining groups (1, 2, 3) is also clockwise, which gives it an R configuration.
Step 5: Conclusion
Since both stereocenters are R, the compound is correctly designated as (2R,3R)-2,3-butanediol.
Therefore, the correct answer is option A.
---
Butanediol has the formula C4H10O2 and consists of a four-carbon chain with hydroxyl (-OH) groups attached to the 2nd and 3rd carbon atoms. The structure can be represented as follows:
In (2R,3R)-2,3-butanediol, the stereocenters are at the 2nd and 3rd carbon atoms. Each of these carbons is attached to four different groups, which allows us to assign R or S configurations.
Using the Cahn-Ingold-Prelog priority rules, we assign priorities to the substituents attached to the stereocenters:
- -OH (hydroxyl group) has the highest priority (1)
- -CH3 (methyl group) has the next priority (2)
- -CH2- (the carbon chain) has the next priority (3)
- The hydrogen atom (H) has the lowest priority (4)
- -OH (hydroxyl group) has the highest priority (1)
- -CH3 (methyl group) has the next priority (2)
- -CH2- (the carbon chain) has the next priority (3)
- The hydrogen atom (H) has the lowest priority (4)
To determine the configuration (R or S), we look at the arrangement of the groups:
- For carbon 3, if we position the lowest priority group (H) at the back, the order of the remaining groups (1, 2, 3) is also clockwise, which gives it an R configuration.
Since both stereocenters are R, the compound is correctly designated as (2R,3R)-2,3-butanediol.
Topper's Solved these Questions
- ISOMERISMBOOK - HIMANSHU PANDEYCHAPTER - ISOMERISMEXERCISE - Level 3 (Q.26 To Q.50)
25 Videos
- ISOMERISMBOOK - HIMANSHU PANDEYCHAPTER - ISOMERISMEXERCISE - Level 3 (Q.51 To Q.75)
25 Videos
- ISOMERISMBOOK - HIMANSHU PANDEYCHAPTER - ISOMERISMEXERCISE - Level 2 (Q.51 To Q.55)
5 Videos
- HALIDESBOOK - HIMANSHU PANDEYCHAPTER - HALIDESEXERCISE - Subjective Type Problems
10 Videos
- NOMENCLATUREBOOK - HIMANSHU PANDEYCHAPTER - NOMENCLATUREEXERCISE - Section Iv (Q.26 To Q.26)
1 Videos
Similar Questions
Knowledge Check
If in a triangle (r2−r1)(r3−r1)=2r3r3 then the triangle is :-
Aright angledBisosecelsCequilateralDnone of theseStatement 1: in a ΔABC if a<b<c and r inradius and r1,r2,r3 are the exradii opposite to angle r>r1>r2>r3 respectively then
Statement 2: For , ΔABCr1r2+r2r3+r3r1=r1r2r3rAIf statement -1 is true, statement –II is true, statement –II is a correct explanation for statement-IBIf statement –I is true, statement –II is true, statement –II is not a correct explanation for statement –ICIf statement –I is true, statement –II is falseDIf statement –I is false, statement –II is truer2r3=
AStanA2BScotA2CSsinA2DScosA2
In ΔABC if r1=2r2=3r3 and D is the mid point of BC then cos∠ADC=
View SolutionLet n be a positive integer and
Δr=∣∣ ∣ ∣∣r2+rr+1r−22r2+3r−13r3r−3r2+2r+32r−12r−1∣∣ ∣ ∣∣ and
n∑r=1Δr=an2+bn+c find the value of a+b+c.
View SolutionIf Dr=∣∣ ∣ ∣ ∣∣rxn(n+1)22r1n23r−2n(3n−1)2∣∣ ∣ ∣ ∣∣ then n∑r=1Dr=0
View SolutionIn a ΔABC, if r1=2r2=3r3, then show that ab=54.
View SolutionLet R be a relation defined on A={1,2,3} by :
R={(1,3),(3,1),(2,2)}. R is :
View Solution
