23592U+n→23592U→ fission product + Neutron 3.20×10−11J.
The energy released when 1 g of 23592U undergoes fission is Solution in Kannada
12.75×108kJ
18.60×109kJ
8.21×107kJ
6.55×106kJ
The correct Answer is:C
Step by step video, text & image solution for ""_(92)^(235)U+nto""_(92)^(235)Uto fission product + Neutron 3.20xx10^(-11)J. The energy released when 1 g of ""_(92)^(235)U undergoes fission is by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which of the following substance has highest proton affinity ?
View SolutionThe IUPAC name of
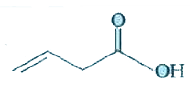 is :
is :
View SolutionWhen ._(92)U^(235) undergoes fission, 0.1% of the original mass is released into energy. How much energy is released by an atom bomb which contains 10kg of ._(92)U^(235) ?
View Solution(a) Calculate the energy released by the fission of 2g of ._(92)U^(235) in kWh . Given that the energy released per fission is 200MeV . (b) Assuming that 200MeV of enrgy is released per fission of uranium atom, find the number of fissions per second required to released 1 kilowatt power. (c) Find the amount of energy produced in joules due to fission of 1g of ._(92)U^(235) assuming that 0.1% of mass is transformed into enrgy. ._(92)U^(235) = 235 amu , Avogadro number = 6.023 xx 10^(23)
View SolutionThe ._(92)^(235)U absorbs a slow neutron (thermal neutron) & undergoes a fission represented by (i) The energy release E per fission. (ii) The energy release when 1g of ._(92)^(236)U undergoes complete fission. Given : ._(92)^(235)U = 235.1175 am u (atom), ._(56)^(141)Ba = 140.9577 am u (atom), ._(36)^(92)Kr = 91.9264 am u (atom), ._(0)^(1)n = 1.00898 am u .
View SolutionCalculate the energy released by fission of 1 g of .23592U, assuming that an energy of 200 MeV is released by fission of each atom of .235U. (Avogardo constant is =6.023×1026kgmol−1)
View SolutionU235+n1→ fission product + neutron + 3.2×10−11j. The energy released , when 1g of u235 finally undergoes fission , is
View Solution._(92)U^(235) + n rarr fission product + neutron + 3.20 xx 10^(-11) J . The energy released when 1g of ._(92)U^(235) undergoes fission is
View Solutionजब 23592U का विखण्डन होता है तो इसके प्रारम्भिक द्रव्यमान का 0.1% ऊर्जा के रूप में बदल जाता है | यदि 1 किग्रा 23592U का विखण्डन होता है तो उत्पन्न ऊर्जा होगी :
View Solution23592U+10n→23692U→विखण्डित उत्पाद + न्यूट्रॉन +.....3.20x10−11 जूल जब 1 ग्राम 23592U विखण्डित होगा, तो कितनी ऊर्जा निकलेगी?
View SolutionAssertion (A) Fragments produced in the fission of 92U235 are radioactive.
Reason (R) The fragments in the fission of 235U have a proton to neutron ratio of 2.5.
View SolutionThe energy released when one nucleus of .92u235 undergoes fission is 188 MeV. The energy released when 100g of undergoes fission is .92u235
View SolutionCalculate the amount of energy released when 1 kg of 23592U undergoes fission reaction.
View SolutionNuclides of 23592U can undergoes nuclear fission when bombarded by ............... .
View SolutionThe number of neutrons in ""_(92)U^(235) is
View Solution
