A 10-L vessel filled with O2 at 300 K is connected to an open limb manometer containing glycerine. The level in the open limb was found to be higher than the other limb by 50 cm. Calculate the number of moles of the gas in the vessel (Given dglycerine=2.72gmL−1,dHg=13.6gmL−1)
To solve the problem of calculating the number of moles of oxygen gas in a 10-L vessel at 300 K, we will follow these steps:
Step 1: Understand the Manometer Setup
The manometer is used to measure the pressure of the gas in the vessel. Since the level of glycerine in the open limb is higher than in the limb connected to the gas, we know that the pressure of the gas is greater than atmospheric pressure.
Step 2: Calculate the Pressure Difference
We need to convert the height difference of 50 cm of glycerine into pressure. The pressure can be calculated using the formula:
P=h⋅d⋅g
Where:
- P is the pressure,
- h is the height difference (in meters),
- d is the density of glycerine,
- g is the acceleration due to gravity (approximately 9.81m/s2).
First, convert the height from cm to meters:
h=50cm=0.50m
Next, we need the density of glycerine, which is given as dglycerine=2.72g/mL or 2.72×1000kg/m3=2720kg/m3.
Now we can calculate the pressure difference:
Pglycerine=0.50m×2720kg/m3×9.81m/s2
Pglycerine=0.50×2720×9.81=13343.76Pa
Step 3: Convert Pressure to mmHg
To convert the pressure from Pascals to mmHg, we use the conversion factor 1mmHg=133.322Pa:
Pglycerine=13343.76Pa133.322Pa/mmHg≈100.0mmHg
Step 4: Calculate Total Pressure in the Vessel
The total pressure in the vessel is the atmospheric pressure plus the pressure difference due to the manometer. Assuming atmospheric pressure Patm=760mmHg:
Ptotal=Patm+Pglycerine=760mmHg+100.0mmHg=860mmHg
Step 5: Convert Total Pressure to Atmospheres
To use the ideal gas law, we need to convert mmHg to atmospheres:
Ptotal=860mmHg760mmHg/atm≈1.13atm
Step 6: Use Ideal Gas Law to Calculate Moles
The ideal gas law is given by:
PV=nRT
Where:
- P = pressure in atm,
- V = volume in liters,
- n = number of moles,
- R = ideal gas constant 0.0821L⋅atm/(K⋅mol),
- T = temperature in Kelvin.
Rearranging for n:
n=PVRT
Substituting the values:
n=(1.13atm)(10L)(0.0821L⋅atm/(K⋅mol))(300K)
Calculating:
n=11.324.63≈0.46moles
Final Answer
The number of moles of oxygen gas in the vessel is approximately 0.46 moles.
---
The manometer is used to measure the pressure of the gas in the vessel. Since the level of glycerine in the open limb is higher than in the limb connected to the gas, we know that the pressure of the gas is greater than atmospheric pressure.
We need to convert the height difference of 50 cm of glycerine into pressure. The pressure can be calculated using the formula:
P=h⋅d⋅g
Where:
- P is the pressure,
- h is the height difference (in meters),
- d is the density of glycerine,
- g is the acceleration due to gravity (approximately 9.81m/s2).
h=50cm=0.50m
Pglycerine=0.50m×2720kg/m3×9.81m/s2
Pglycerine=0.50×2720×9.81=13343.76Pa
To convert the pressure from Pascals to mmHg, we use the conversion factor 1mmHg=133.322Pa:
Pglycerine=13343.76Pa133.322Pa/mmHg≈100.0mmHg
The total pressure in the vessel is the atmospheric pressure plus the pressure difference due to the manometer. Assuming atmospheric pressure Patm=760mmHg:
Ptotal=Patm+Pglycerine=760mmHg+100.0mmHg=860mmHg
To use the ideal gas law, we need to convert mmHg to atmospheres:
Ptotal=860mmHg760mmHg/atm≈1.13atm
The ideal gas law is given by:
PV=nRT
Where:
- P = pressure in atm,
- V = volume in liters,
- n = number of moles,
- R = ideal gas constant 0.0821L⋅atm/(K⋅mol),
- T = temperature in Kelvin.
n=PVRT
Substituting the values:
n=(1.13atm)(10L)(0.0821L⋅atm/(K⋅mol))(300K)
n=11.324.63≈0.46moles
The number of moles of oxygen gas in the vessel is approximately 0.46 moles.
Topper's Solved these Questions
- STATES OF MATTER : GASES AND LIQUIDESBOOK - PRADEEPCHAPTER - STATES OF MATTER : GASES AND LIQUIDESEXERCISE - TEST YOUR GRIP
27 Videos
- STATES OF MATTER : GASES AND LIQUIDESBOOK - PRADEEPCHAPTER - STATES OF MATTER : GASES AND LIQUIDESEXERCISE - FILL IN THE BLANK
20 Videos
- STATES OF MATTER : GASES AND LIQUIDESBOOK - PRADEEPCHAPTER - STATES OF MATTER : GASES AND LIQUIDESEXERCISE - CURIOSITY QUESTION
17 Videos
- SOME p-BLOCK ELEMENTSBOOK - PRADEEPCHAPTER - SOME p-BLOCK ELEMENTSEXERCISE - Competition Focus (JEE( Main and Advanced)/Medical Entrance) VIII. Assertion-Reason Type Questions (Type I)
23 Videos
- STATES OF MATTER: SOLID MATTERBOOK - PRADEEPCHAPTER - STATES OF MATTER: SOLID MATTEREXERCISE - COMPETITION FOCUS (ASSERTION-REASON)
17 Videos
Similar Questions
A gas is filled into a bulb connected to an open limb manometer. The level of mercury in the open arm is 2.1 cm lower than that in the other arm of the manometer. The atmospheric pressure is 740 mm. What is the pressure of the gas?
View SolutionA gas is filled into a bulb connected to an open limb manometer. The level of mercury in the open arm is 2.1 cm lower than that in the other arm of the manometer. The atmospheric pressure is 740 mm. What is the pressure of the gas?
View Solution
Knowledge Check
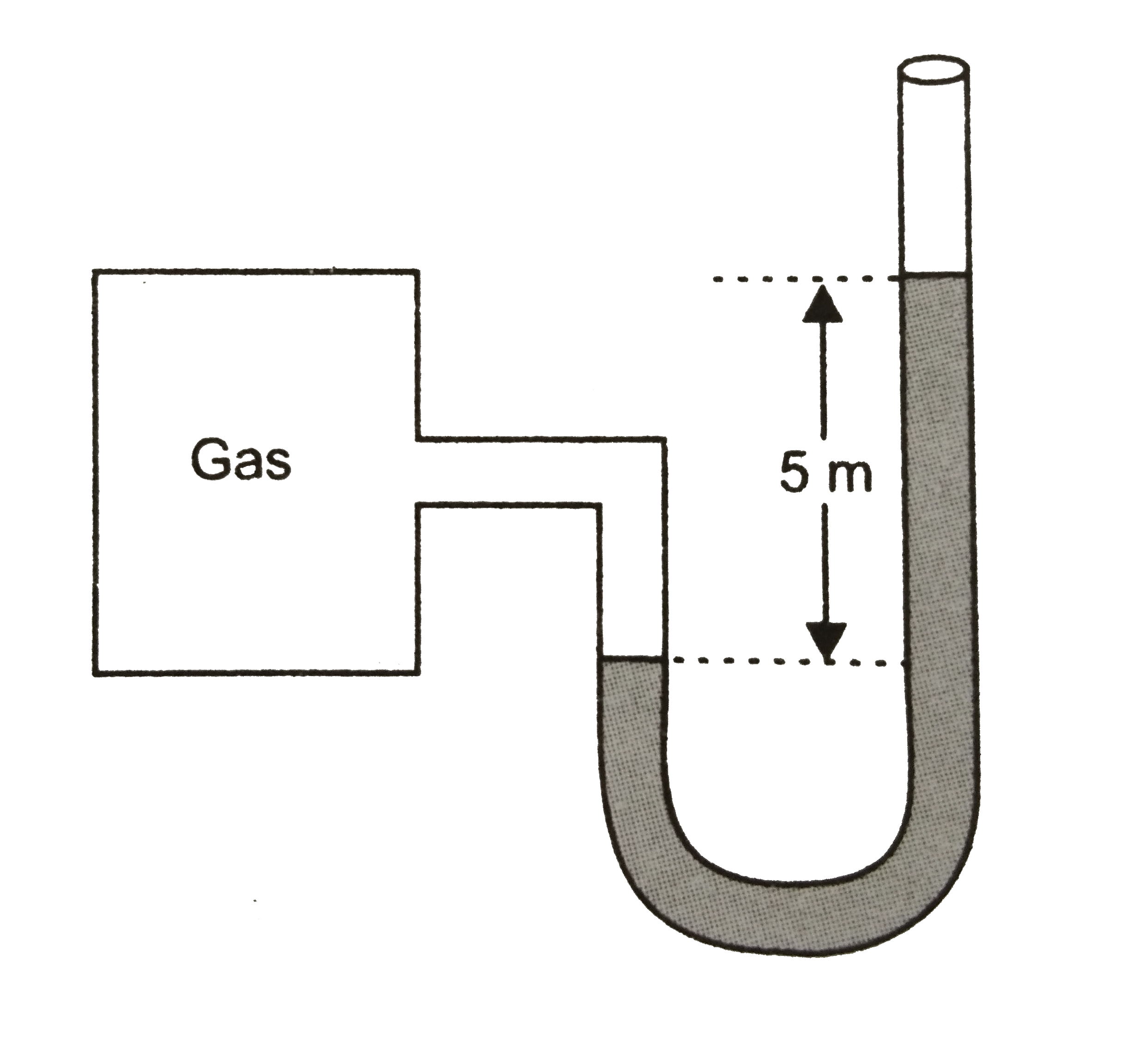
A gas jar of 10 litre volume filled with O2 at 300 K is connected to glycerine manometer. The maonometer shows 5 m difference in the level as shown in figure. What will be the number of moles of O2 in the gas jar ?
(Given dglycerine=272g/mL,dmercury=13.6g/mL)A0.64molB0.4molC0.94molD0.36molCalculate the number of moles of gas present in the container of volume 10 L at 300 K, if the manometer containing glycerine shows 5 m difference in level as shown diagram.
(Given : dglycerin=2.72g/mL, dmercury=13.6g/mL)
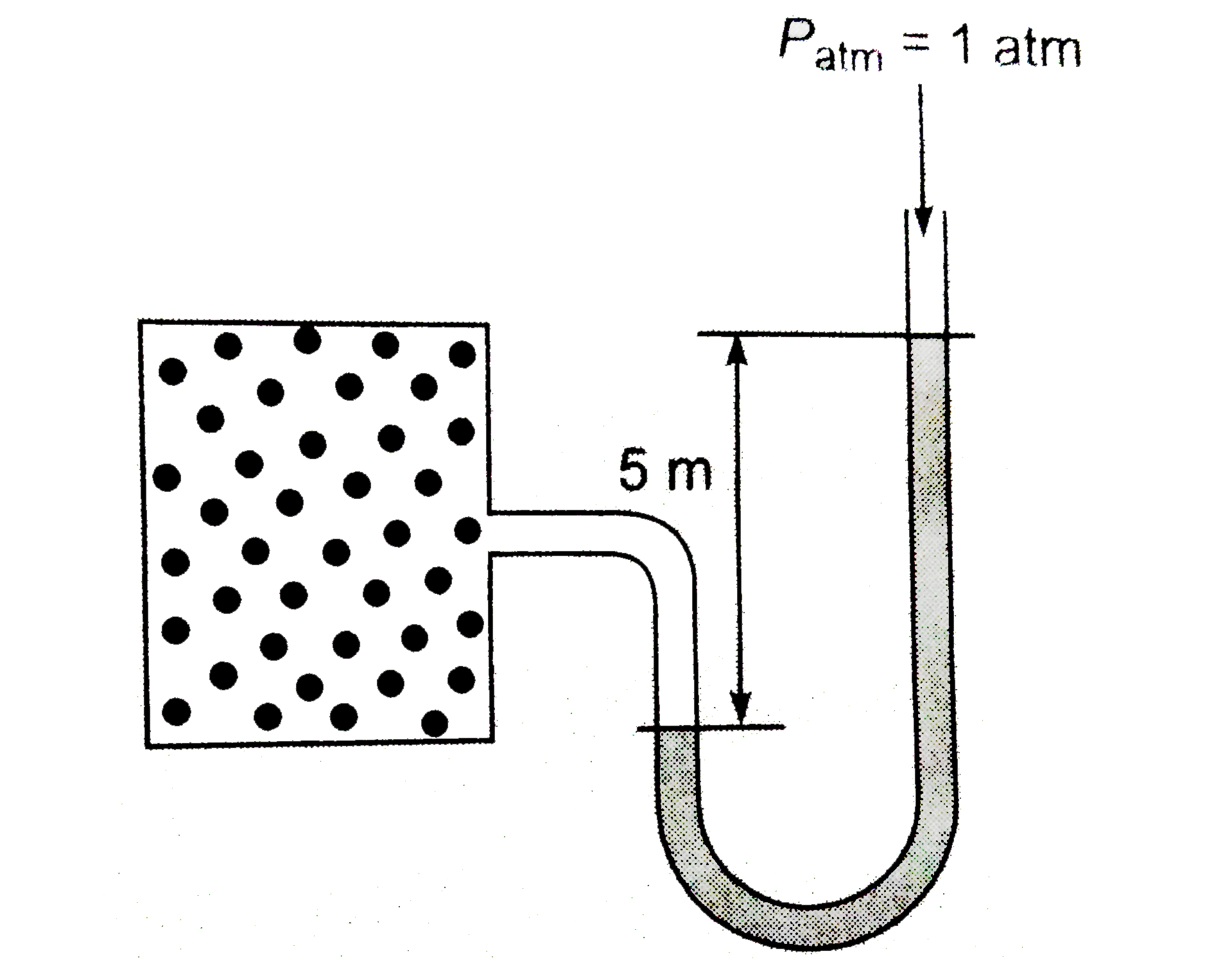 A0.94 moleB0.49 moleC0.64 moleDnone of these
A0.94 moleB0.49 moleC0.64 moleDnone of theseA closed 10 L vessel contains 1 L water gas (1:1 CO:H2) and 9 L air (20% O2 by volume) at STP. The contents of the vessel are ignited. The number of moles of CO2 in the vessel is closest to :
A0.22B0.022C0.9D3.6
A manometer is connected to a gas containing bulb. The level of mercury in open arm is 2.6 cm lower than that in the other arm of the manometer. What is the pressure of the gas if the atmospheric pressure is 752 mm Hg?
View SolutionOne of the limbs of a mercury manometer is connected to a gas cylinder. The mercury level in the limb connected to the gas cylinder is 10 cm higher than that in the other limb. Then the gauge pressure of the gas is ____ cm of Hg.
View SolutionOne of the limbs of a mercury manometer is connected to a gas cylinder. The mercury level in the limb connected to the gas cylinder is 10 cm higher than that in the other limb. Then the gauge pressure of the gas is _______ cm of Hg.
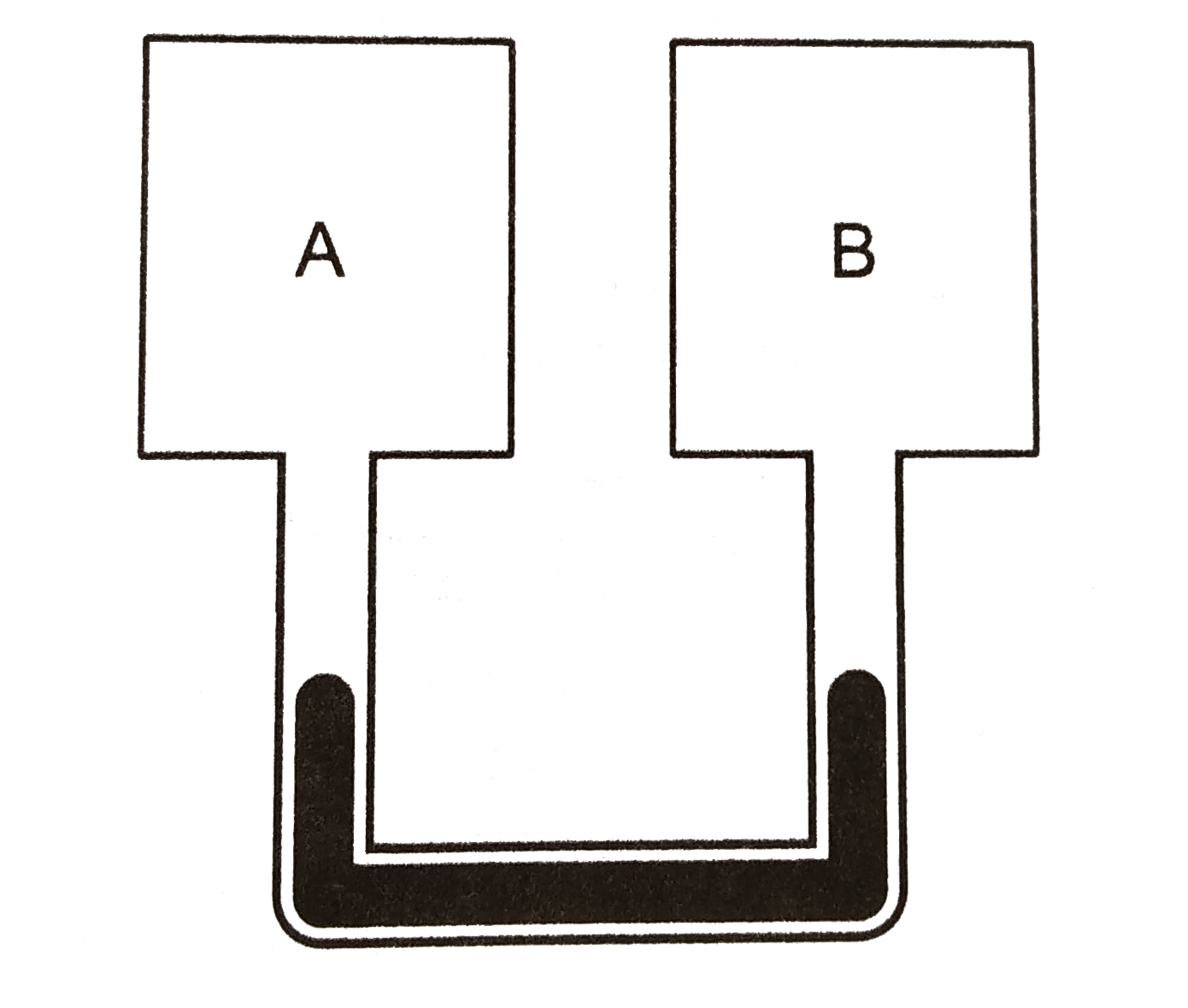
View SolutionFigure shows two rigid vessels A and B, each of volume 200cm3 containg an ideal gas (Cv=12.5JK−1mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm mercury and the temperature is 300k. (a) (5−0J) of heat is supplied to the gas in the vessels.(b) (10J) to the gas in the vessels B. Assuming no appreciable transfer of heat from A to B calculate the dufference in the heights of mercury in the two sides of the manometer. Gas constant (R=8.3JK−1mol−1)
View SolutionA glass bulb contains 2.24LofH2 and 1.12L of D2 at STP. It is connected a fully evacuated bulb by a stop-cock with a small opening. The stop-cock is opened for sometime and then closed. The first bulb now contains 0.10g of H2. The percentage of H2 in the mixture is
View Solution
