a. Calculate the packing efficiency in a Body Centered Cubic (BCC) lattice.
b. Silver forms a ccp lattice. The edge length of its unit cell is 408.6 pm. Calculate the density of silver. Solution in Kannada
bcc diagram.
Edge length
Packing efficiency
Detailed Answer:
Packing efficiency in body centred cubic (bcc) lattice.
The number of atoms per unit cell in bcc is two.
So, the volume of two atoms (two spheres)
Let the edge length a. be the radius of the sphere.
The body diagonal
and face diagonal ,
Then
In
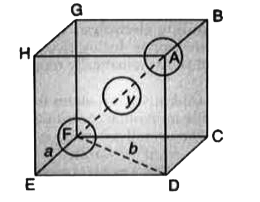
Now in
But
Volume of unit cell
Paking efficiency
Topper's Solved these Questions
- SOLVED PAPER II PUC APRIL-2016 BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER II PUC APRIL-2016 EXERCISE - PART-C
13 Videos
- Solved Paper 4 BOOK - OSWAAL PUBLICATIONCHAPTER - Solved Paper 4 EXERCISE - exercise
62 Videos
- SOLVED PAPER II PUC JULY - 2016BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER II PUC JULY - 2016EXERCISE - PART -E
19 Videos
Similar Questions
In the extraction of Aluminimum by electrolysis.
i. Give the composition of electrolyte used
ii. Overall cell reaction
iii. Role of cryolite
View SolutionState Henry's law.
View SolutionExplain SN2 mechanism taking an example of chloromethane.
View SolutionSilver froms ccp lattice and X-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver (atomic mass =107.9u).
View SolutionSilver froms ccp lattice and X-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver (atomic mass =107.9u).
View Solutionचाँदी घनीय संवृत संकुलन (ccp) जालक बनाती है | इसके क्रिस्टल की X-किरण जाँच से ज्ञात हुआ कि इसके एकक सेल के कोर कि लम्बाई 408.6 pm है | चाँदी के घनत्व कि गणना कीजिए | (चाँदी का परमाणु द्रव्यमान = 107.9)
View SolutionSilver crystallizes in CCP lattice. The edge length of its unit cell is 408.6 pm. Calculate density of silver (atomic mass of silver is 107.9)
View SolutionSilver crystallizes in CCP lattice. The edge length of its unit cell is 408.6 pm. Calculate density of silver (atomic mass of silver is 107.9)
View Solution(a) calculate packing efficiency in simple cubic lattice. (b) An element having atomic mass 107.9 u has FCC lattice . The edge length of its unit cell is 408.6 pm calculate density of the unit cell. Given, NA=6.022xx10^23 mol-1] .
View SolutionSilver forms ccp lattice and x-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver. (Atomic mass of Ag = 107.9 u)
View SolutionSilver forms ccp lattice and X-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver
(Atomic mass = 107.9 u).
View SolutionSilver forms ccp lattice and x-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver. (Atomic mass of Ag = 107.9 u)
View SolutionSilver forms ccp lattice and x-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver. (Atomic mass of Ag = 107.9 u)
View SolutionAn element having atomic mass 107.9 u has FCC lattice. The edge length of its unit cell is 408.6 pm. Calculate density of the unit cell.
[Given, NA=6.022×1023mol−1].
View SolutionSilver forms ccp lattice and X-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver (atomic mass=107.94)
View SolutionSilver forms ccp lattice and X-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver (Atomic mass = 107.9 u).
View Solution
