A closed tank is first evacuated and then connected to a 50 L cylinder containing compressed nitrogen gas. The gas pressure in the cylinder originally at 20.5 bar falls to 11.2 bar after it is connected to the evacuated tank. Calculate the volume of the tank.
The correct Answer is:41.5 L
To solve the problem, we will use the ideal gas law and the concept of conservation of moles. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Scenario
We have a closed tank that is initially evacuated (meaning it has no gas inside). Then, a 50 L cylinder containing nitrogen gas at a pressure of 20.5 bar is connected to the tank. After the connection, the pressure in the cylinder drops to 11.2 bar.
Step 2: Identify the Variables
- Initial pressure in the cylinder (P1) = 20.5 bar
- Final pressure in the cylinder (P2) = 11.2 bar
- Volume of the cylinder (V1) = 50 L
- Volume of the tank (V2) = ? (this is what we need to find)
Step 3: Use the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = ideal gas constant
- T = temperature (assumed constant)
Step 4: Calculate the Number of Moles Initially
Initially, when the nitrogen gas is in the cylinder, the number of moles of nitrogen gas can be calculated using the initial pressure and volume:
n=P1V1RT
Step 5: Calculate the Number of Moles After Connection
After the tank is connected, the total volume becomes V1+V2 and the pressure is now P2. The number of moles of nitrogen gas can be expressed as:
n=P2(V1+V2)RT
Step 6: Set Up the Equation
Since the number of moles of nitrogen gas remains constant before and after the connection, we can set the two equations equal to each other:
P1V1RT=P2(V1+V2)RT
Step 7: Cancel Out Common Terms
The RT terms on both sides can be canceled out:
P1V1=P2(V1+V2)
Step 8: Substitute Known Values
Substituting the known values into the equation:
20.5×50=11.2×(50+V2)
Step 9: Solve for V2
Now, we can solve for V2:
1. Calculate the left side:
20.5×50=1025
2. Expand the right side:
11.2×(50+V2)=560+11.2V2
3. Set the equation:
1025=560+11.2V2
4. Rearranging gives:
1025−560=11.2V2
465=11.2V2
5. Finally, solve for V2:
V2=46511.2≈41.5 L
Conclusion
The volume of the tank is approximately 41.5 L.
We have a closed tank that is initially evacuated (meaning it has no gas inside). Then, a 50 L cylinder containing nitrogen gas at a pressure of 20.5 bar is connected to the tank. After the connection, the pressure in the cylinder drops to 11.2 bar.
- Initial pressure in the cylinder (P1) = 20.5 bar
- Final pressure in the cylinder (P2) = 11.2 bar
- Volume of the cylinder (V1) = 50 L
- Volume of the tank (V2) = ? (this is what we need to find)
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = ideal gas constant
- T = temperature (assumed constant)
Initially, when the nitrogen gas is in the cylinder, the number of moles of nitrogen gas can be calculated using the initial pressure and volume:
n=P1V1RT
After the tank is connected, the total volume becomes V1+V2 and the pressure is now P2. The number of moles of nitrogen gas can be expressed as:
n=P2(V1+V2)RT
Since the number of moles of nitrogen gas remains constant before and after the connection, we can set the two equations equal to each other:
P1V1RT=P2(V1+V2)RT
The RT terms on both sides can be canceled out:
P1V1=P2(V1+V2)
Substituting the known values into the equation:
20.5×50=11.2×(50+V2)
Now, we can solve for V2:
1. Calculate the left side:
20.5×50=1025
2. Expand the right side:
11.2×(50+V2)=560+11.2V2
3. Set the equation:
1025=560+11.2V2
4. Rearranging gives:
1025−560=11.2V2
465=11.2V2
5. Finally, solve for V2:
V2=46511.2≈41.5 L
The volume of the tank is approximately 41.5 L.
Topper's Solved these Questions
- STATES OF MATTER : GASES AND LIQUIDSBOOK - MODERN PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Advanced Level (PROBLEMS)
14 Videos
- STATES OF MATTER : GASES AND LIQUIDSBOOK - MODERN PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Conceptual Questions (1)
17 Videos
- STATES OF MATTER : GASES AND LIQUIDSBOOK - MODERN PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - UNIT PRACTICE TEST
13 Videos
- SOME BASIC CONCEPTS OF CHEMISTRY BOOK - MODERN PUBLICATIONCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRY EXERCISE - COMPETITION FILE (INTEGER TYPE AND NUMERICAL VALUE TYPE QUESTIONS)
10 Videos
- STRUCTURE OF ATOMBOOK - MODERN PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Unit Practice Test
13 Videos
Similar Questions
A large irregularly-shaped closed tank is first evacuated and then connected to a 50-litre cylinder containing compressed nitrogen gas. The gas pressure in the cylinder, originally at 21.5 atm, falls to 1.55 atm after it is connected to the evacuated tank. Calculate the volume of the tank.
View SolutionA certain mass of a gas taken in 1 L cylinder exerts a pressure of 500 mm Hg at a certain temperature. If the gas is transferred to another cylinder where it exerts 20 per cent more pressure, calculate the volume of the cylinder at the same temperature.
View Solution
Knowledge Check
A container of 1.0 L capacity filled with 1.0 mole of ideal gas is connected to an evacuated vessel to 9L. Calculate change in entropy. (R=1.987 cal.)
A0.188 cal ⋅K−1mol−1B0.4576 ⋅K−1mol−1C4.576 cal⋅K−1mol−1D4.366 cal⋅K−1mol−1A cylinder of 5 L capacity, filled with air at NTP is connected with another evacuated cylinder of 30 L capacity. The resultant air pressure in both the cylinders will be
A10.8 cm of HgB14.9 cm of HgC21.8 cm of HgD38.8 cm of HgA non - conducting piston of mass m and are S0 divides a non - conducting, closed cylinder as shown in the figure. A piston having mass m is connected with the top wall of the cylinder by a spring of force constant k. The top part is evacuated and the bottom part is evacuated and the bottom part contains an ideal gas at a pressure P0 in the equilibrium position. Adiabatic exponent γ and in equilibrium length of each part is l. (neglect friction). Find the angular frequency for small oscillation.
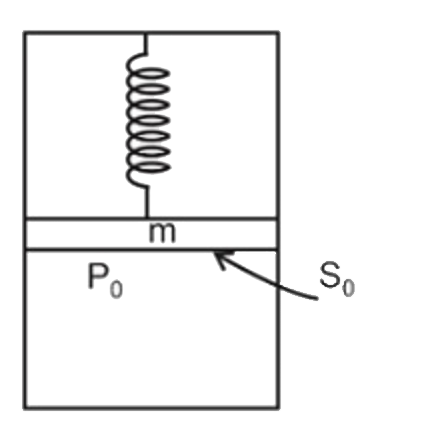 A√kl+γP0S02mlB√3kl+γP0S0mlC√kmD√kl+γP0S0ml
A√kl+γP0S02mlB√3kl+γP0S0mlC√kmD√kl+γP0S0ml
An L.P.G cylinder contains 15kg of butane gas at 27∘C and 10 atm pressure It was leaking and its pressure fell down to 8 atm pressure after one day Calculate the amount of leaked gas .
View SolutionA bulb A containing gas at 1.5 bar pressure was connected to an evacuated vessel of 1.0 dm3 capacity through a stopcock. The final pressure of the system dropped to 920 mbar at the same temperature. What is the volume of the container A?
View SolutionA cylinder of compressed gas contains nitrogen and oxygen in the molar ratio of 3:1. If the cylinder contains 2.5×104g of oxygen, what is the total mass of the gas in the mixture ?
View SolutionA cylinder of compressed gas contains nitrogen and oxygen in the ratio 3:1 by mole. If the cylinder is known to contain 2.5×104g of oxygen, what is the total mass of the gas mixture?
View SolutionA bulb 'X' of unknown volume containing a gas at one atmospheric pressure is connected to an evacuated bulb of 0.5 litre capacity through a stop -cock. On opening the stop-cock, the pressure in the whole system after some time was found to have a constant value of 570 mm at the same temperature. What is the volume of the bulb X ?
View Solution
